分离链接法(Separate Chaining)

之前我们说过，对于需要动态维护的散列表 冲突是不可避免的，无论你的散列函数设计的有多么精妙。因此我们解决的重要问题就是：一旦发生冲突，我们该如何加以排解？

我们在这里讨论最常见的两种方法：分离链接法和开放定址法。本篇探讨前者，下一篇讨论后者。

分离链接法

解决冲突的第一种方法通常叫做分离链接法（separatechaining），做法是将散列到同一个值的所有元素保留到一个链表中。那……为什么要这么做呢？保留到数组中不行么？下面我们来分析一下。

我们先从最初的思路说起，所谓的冲突形象来说就是一山不容二虎，倘若的确有两只老虎呢？答：用铁丝网将这座山分成两部分，两只老虎各居一侧，这是最朴素的办法了，这种思路也就是多槽位法（multipleslots）。如果此前的桶单元对应于山，那么每一个槽位（slot）就对应于在这个山中用铁丝网分割出的一个子区域。

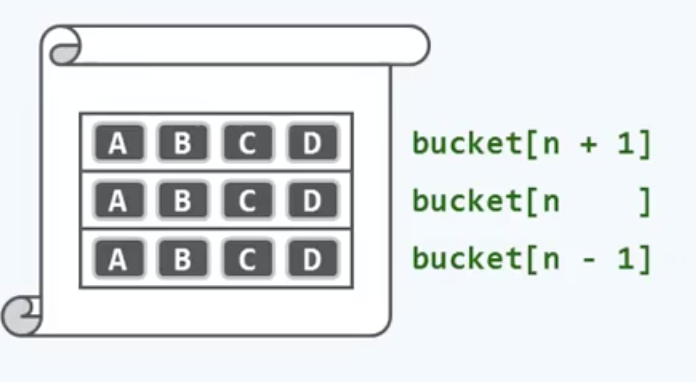
对于这个散列表，每一个横条就是一个一个又一个的桶单元。在这里，我们将每个桶单元都继续细分为ABCD，4个槽位，每个桶内部的这些槽位就可以用来存放彼此冲突的若干个词条。

具体看一个例子吧，比如这就是一个长度为23的散列表，其中每一个桶都被分成了3个槽位

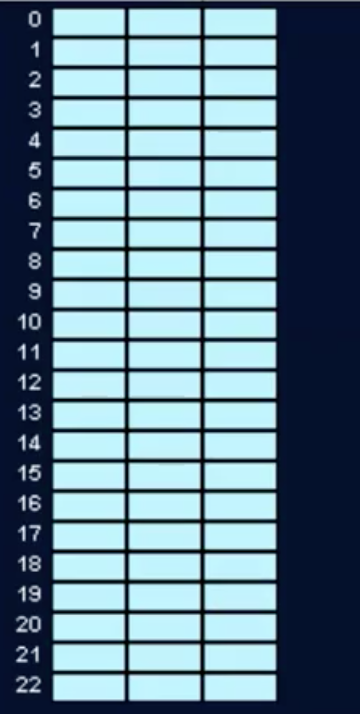
往里面放入数据之后变成这样：

可以看到这里尽管有些词条的确会彼此冲突，但依然可以在对应的桶中和平共处，被分隔开。当然，查找过程需要多出一步：除了需要根据关键码确定对应的桶单元地址，还需要在桶中遍历所有的槽位——直到找到目标or失败。不过只要槽位数量不多，就还能保证O(1）的效率。

但是！有一个显而易见的问题。。。。

找到对应的地址之后，遍历到哪算完啊，我还得往前扫描多久啊？问题就在这：每一个桶具体应该细分为多少个槽位，在事先几乎是无法预测的。如果分的过细就会造成空间上的浪费，而反过来，无论分的多细，在极端的情况下，仍有可能在某个特定的桶中发生大规模的冲突。那么面临这一两难的抉择该如何破解呢？

多槽位法在空间和时间效率上的两难处境，我在学习向量（动态数组）的时候也遇到过，那时的解决办法就是用列表（这里就采用指针链表实现）。

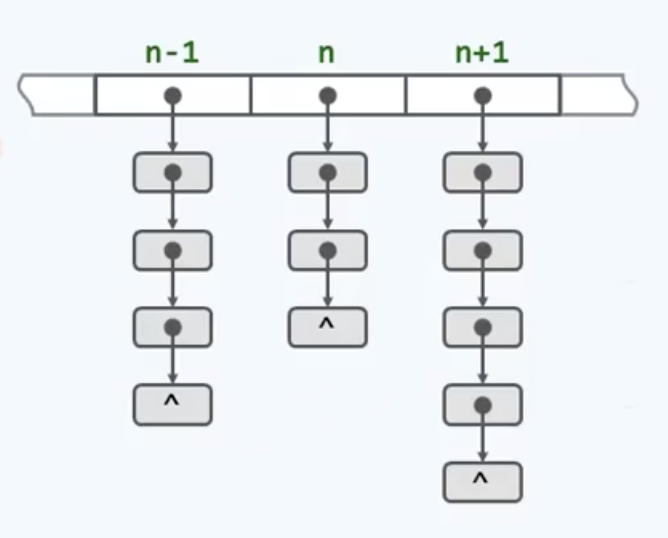
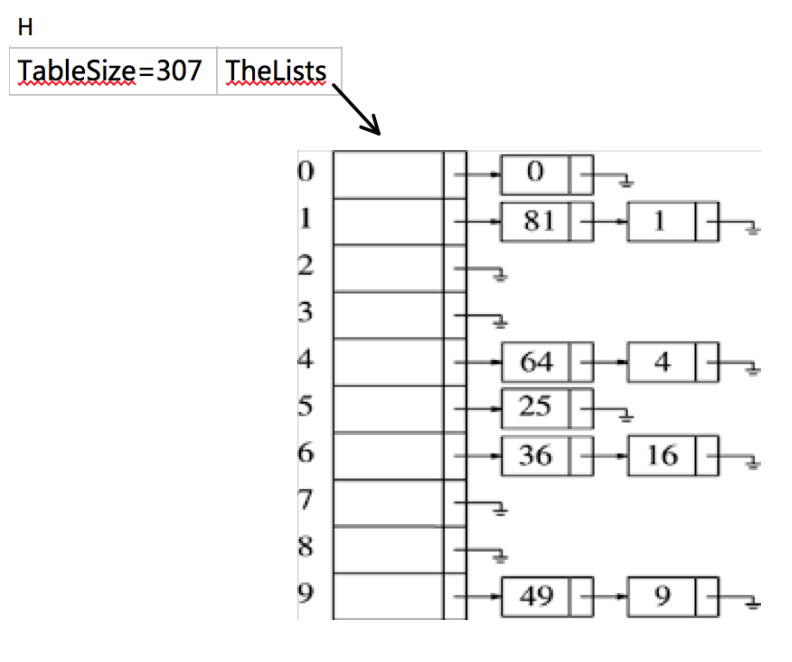
新的策略如这幅图所示：如果这个长条是整个散列表，那么其中的每一个单元都将各自拥有一个对应的列表，而每一个列表都可以用来存放一组彼此冲突的词条。那么答案就水落石出了——将相互冲突的词条串接起来，也就是所谓的separate chaining。举个例子：

这里我们假设关键字是前10个完全平方数，hash(x)=x%10，这里Size不是素数，只是为了简便。

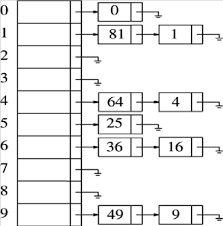
相对于多槽位法，独立链法的优势非常明显：除了最初的表头，我们无需预留任何更多的空间，甚至如果空间很紧，更可取的方法是避免使用这些表头。而且表的长度可以根据需要自由的伸缩，只要系统的资源足够，任意多次的冲突都可以解决。得益于我们之前实现的表结构，我们只需寥寥几句即可实现相应的散列表结构。

下面来谈谈实现策略。

先给出实现分离链接法所需要的类型声明。里面的ListNode结构和之前的链表声明相同，而散列表结构包含一个链表数组（和数组中链表的个数），在散列表结构初始化时动态分配空间。此处的HashTable类型就是指向表头的指针。

#ifndef HashSep_h
#define HashSep_h
struct ListNode;
typedef struct ListNode *Position;
struct HashTb1;
typedef struct HashTb1 *HashTable;

HashTable Init(int Size);
int Delete(int key,HashTable H);
void Insert(int key, HashTable H);
Position Find(int key,HashTable H);
Position FindPre(int key,HashTable H);
int Retrieve(Position P);
#endif /* HashSep_h */

struct ListNode {
    int value;
    Position next;
};

typedef Position List;

/*这里的List *TheLists将会是一个指针数组，用来充当表头，等待后续分配节点。
 这个例子中我们使用表头（有时候空间资源比较紧可以省略表头），虽然这有点浪费。
 */
struct HashTb1 {
    int TableSize;
    List *TheLists;
};

但是有个问题要小心

就是TheList域实际上是一个指向“指向ListNode结构的指针”的指针，二级指针。如果不使用typedef，那可能会相当混乱——毕竟没人想看见代码里出现一堆struct** TheLists这种鬼玩意。

为执行Find，我们要用散列函数来确定究竟考察哪个表。此时我们顺次遍历并返回被查找项所在的位置。为执行Insert，我们要先查查有没有重复的，遍历一下（如果插入重复元素，通常要留出一个额外的变量，用来计数，重复元出现时+1）。如果是新元素，那么插到前端或者末尾都行，哪个容易就做哪个hhhh  编写程序时这是最容易寻址的一种方式。有时候新元素插入前端不仅因为方便，而且还因为新被插入的元素被最先访问的可能性最大（我大散列自有国情在此）。

Find思路说清了，开始干吧，先初始化

HashTable Init(int Size){
    HashTable H;
    int i;
    if (Size<MinTableSize) {
        printf("Table Size too small\n");
        return nullptr;
    }
    
    //Allocate table
    H=(HashTable)malloc(Sizeof(struct HashTb1));
    H->TableSize=aPrime;
    
    //Allocate array of lists
    H->TheLists=(List*)malloc(Sizeof(List)*H->TableSize);
    
    //Allocate list headers
    for (i=; i<H->TableSize; i++) {
        H->TheLists[i]=(List)malloc(Sizeof(struct ListNode));
        H->TheLists[i]->next=nullptr;
    }
     return H;
}

这里用到了与栈的数组实现中相同的想法。大概情形如下，做了一个简陋的图233：

不过这个程序里的一个低效之处在于malloc执行了TableSize次，这样写是为了方便直观理解，也可以再循环之前调用一次malloc然后循环里对接，从而减少开销，像这样：

List header=(List)malloc(H->TableSize * Sizeof(struct ListNode));
    //Allocate list headers
    for (i=; i<H->TableSize; i++) {
        //H->TheLists[i]=(List)malloc(Sizeof(struct ListNode));
        H->TheLists[i]=&header[i];
        H->TheLists[i]->next=nullptr;
    }

然后实现Find，对Find（key,H)的调用返回一个指向key的指针。如果key是一个string，那么比较和赋值必须用strcmp和strcpy进行。（以后补充上C++代码的时候就不用这么麻烦的方法了）

Position Find(int key,HashTable H) {
    List L=H->TheLists[Hash(key, H->TableSize)];
    Position P=L->next;
    
    while (P && P->value!=key)
        P=P->next;
    return P;
}

然后说插入新元素，如果插入的项已经存在那我们就什么也不做；否则就插入表的前端。

void Insert(int key, HashTable H) {
    Position p,newCell;
    List L;
    
    p=Find(key, H);
    if (!p) {   //key尚未存在
        newCell=(List)malloc(Sizeof(struct ListNode));
        L=H->TheLists[Hash(key, H->TableSize)];//找到对应的桶，这时（可能）发生冲突了，就往前塞进去一个槽
        newCell->next=L->next;   //这老三步了，装填数据，插入前端
        newCell->value=key;
        L->next=newCell;
    }
}

这里的程序是作为例子方便理解，因此处于表意的目的牺牲了一部分性能，比如这里计算了2次hash函数，多余的计算总是不好的，所以后续还需要进一步优化重写。不过作为例子它的使命已经完成了。

删除的语义是返回被删除的关键字，以便。。。留作念想2333

int Delete(int key,HashTable H) {
    Position cur,pre;
    cur=Find(key, H);
    pre=FindPre(key, H);
    if (cur) {
        pre->next=cur->next;
        cur->next=nullptr;//防止野指针
        free(cur);
    }
    else printf("%d has not been found!\n",key);
    return key;
}

这里的FindPre实现如下：和Find差不多，只是多往后试探了一步（如果用双向链表就不用这样了，双链表的实现在我的github里，右侧边栏有地址）

Position FindPre(int key,HashTable H) {
    List L=H->TheLists[Hash(key, H->TableSize)]; //指向要放的那个桶
    Position P=L->next;

    while (P && P->next->value!=key)
        P=P->next;
    return P;

}

除了链表之外，任何的方案都有可能用来解决冲突：一颗BST甚至另一个散列表均可胜任。但是我们所希翼的是，如果表的Size大，同时hash策略足够好，那么所有的表就会尽可能短。

再做一些细致分析：我们定义散列表的装填因子λ=表中总元素／Size，在上面的例子中，λ=1.0，表的平均长度也是λ。执行find需要的总时间是计算散列函数的O(1）+遍历表的时间。在一次不成功的查找中，遍历的平均数量为λ，不包括最后的null。成功的查找则需要遍历大约1+λ/2个节点（具体的推导步骤我去CLRS上看看，然后附上来），他保证必然会遍历至少一个节点，因为查找成功了，但是我们也希望沿着一个表

中途就能找到匹配元素。这就说明了，表的大小实际上不重要，而装填因子才是最重要的。分离链接散列的一般原则是：使得表的大小尽量与预料的元素个数差不多（λ=1）。正如前面说过的，让表的Size是素数从而保证了一个良好的分布，这也是一个好方法。

所以我们可以看到分离链接是多么智慧的一种方法啊，优雅而巧妙的避开了一个老大难的问题：我到底该留几个槽位？而且保证了插入新元素的常数时间，可以解决任意多次的冲突，只要你内存吃得消，时间足够多，而且有链表作为基础，不会卡在指针调整上，实现起来十分便利……

嗯。。。当然，这种方法的缺点也同样是很明显的，比如需要引入额外的指针，而为了生成或销毁节点，也需要借助动态内存的申请。相对于常规的操作，此类动态申请操作的时间成本大致要高出两个数量级。然而这种方法最大的缺陷还不仅于此，还有系统的缓存功能，在这里每个桶内部的查找都是沿着对应的列表顺序进行的，然而在此之前，不同列表中各节点的插入和销毁次序完全是随机的。因此对于任何一个列表而言，其中的节点在物理空间上，往往不是连续分布的。那系统很难预测你的访问方向了，无法通过有效的缓存加速查找过程。当散列表的规模非常之大，以至于不得不借助IO时，这一矛盾就显得更加突出了。

总结一下分离链接的优劣之处吧

优点：

• 无需为每个桶预留多个槽位
• 可解决任意多次冲突
• 删除操作简单、统一

缺点：

• 指针需要额外空间
• 节点需要动态申请，开销比正常高2个数量级
• 空间未必连续分布，系统缓存几乎失效

第三个缺点是极其致命的，那么为了有效的激活并充分利用系统的缓存功能，我们又当如何继续改进呢？下一篇我们继续探索其中的奥秘hhhhh

ps.转载请注明文章来源，否则会追加法律责任。