【Kernal Support Vector Machine】林轩田机器学习技术

考虑dual SVM 问题：如果对原输入变量做了non-linear transform，那么在二次规划计算Q矩阵的时候，就面临着：先做转换，再做内积；如果转换后的项数很多（如100次多项式转换），那么耗费的时间就比较多。

能否在计算Q矩阵这一步的时候，把transform+inner product合成一步呢？

这里就用到了一些kernel trick。

简单来说：某些特殊形式的transfrom，利用kernel trick就是只用计算一次transform之前的输入向量内积（X'X），transform之后的内积结果可以用X'X来表示，这样计算复杂度就维持在了O(d)。

如下的2nd order polynomial transform为例：

只要能用上kernel trick，所有Z'Z都可以用K(X,X')来代替。

接下来看，如果能使用上kernel trick，计算dual SVM的时候会带来哪些好处。

可以用上K(X,X')的地方有：

（1）计算qn,m的时可以直接用

（2）计算bias b的时候可以用上

（3）当输入一个测试样本的时候，可以直接用上（否则先得做转换，再用求出来的公式）

因此，Kernel SVM的QP过程可以利用kernel trick在各个环节都获得简化。

下面分别介绍几个常用的kernel类型。

General Poly-2 Kernel

上面这种K2 kernel的好处：

（1）在计算上非常简洁，只需要计算一次X'X，加1再平方就OK了。

（2）又不失一般性，因为在QP的过程中，常数项、一次项、二次项前面的系数会随着优化而吃掉

但是K2 kernel前面的系数也不能乱选，因为这影响到了最终的W是多少（即margin definition）

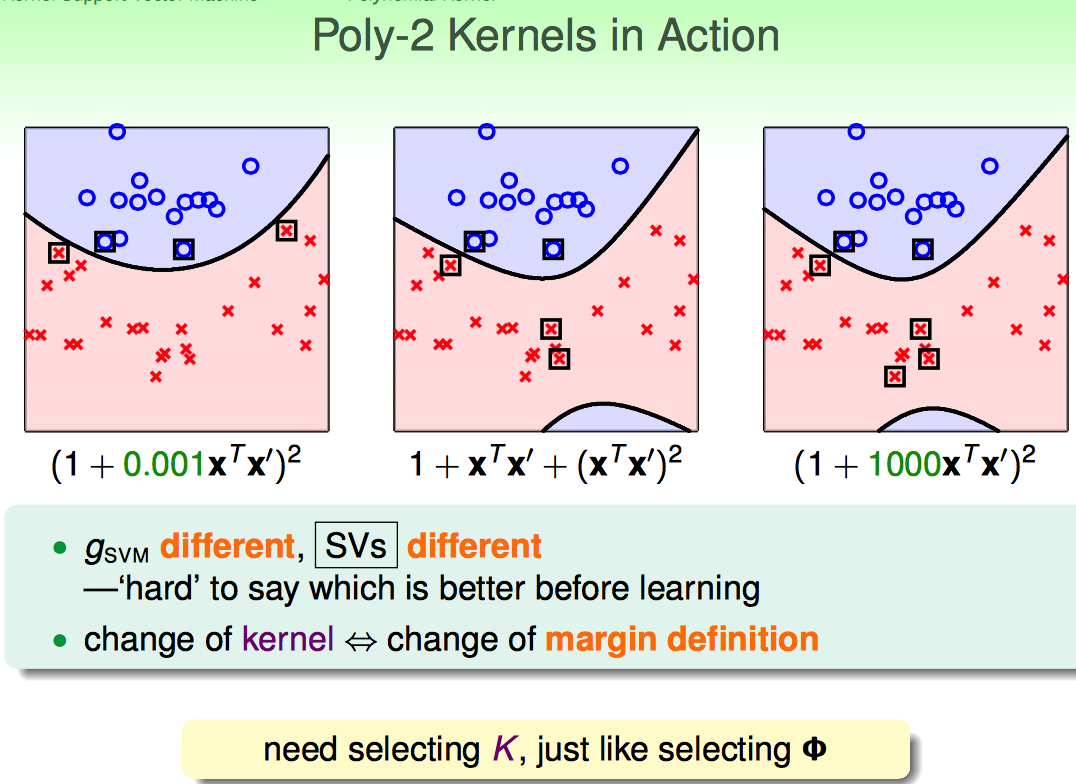
K2不同的系数，选择的SV也不同。

一般先从最简单的SVM开始试验，然后再逐渐复杂。

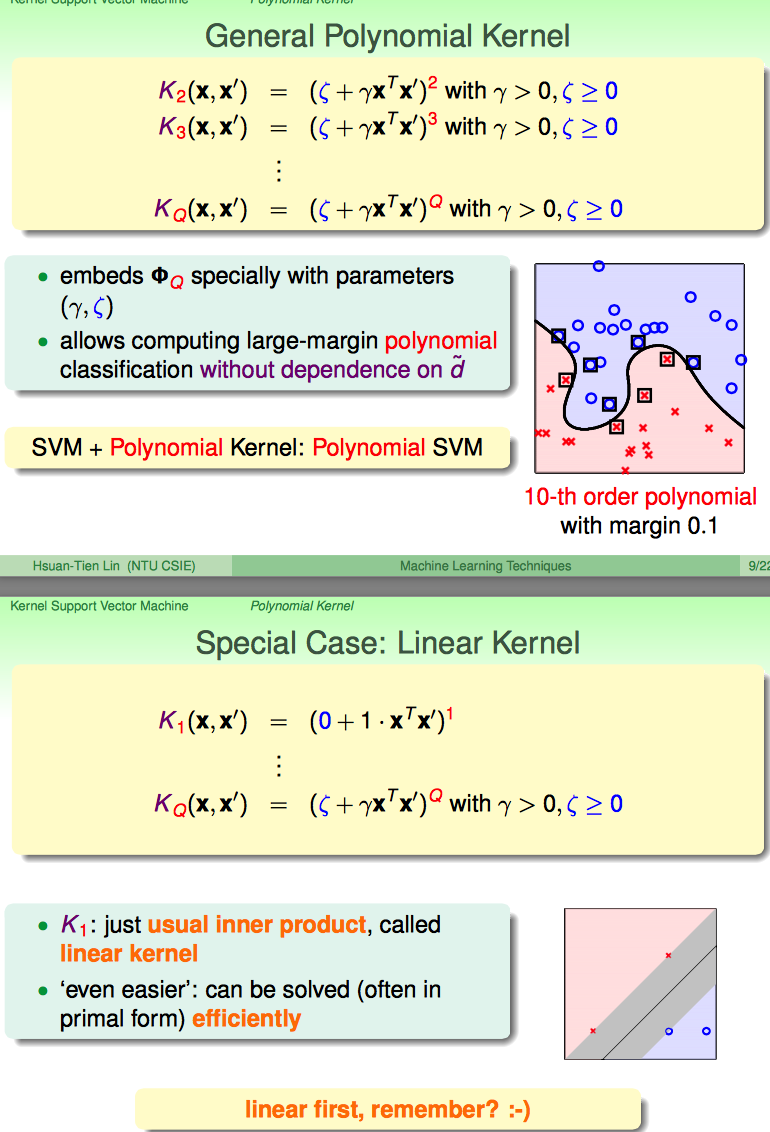
Gaussian SVM

Gaussian SVM是一个无穷维的多项式变换。

无穷维的好处就是学习power增强了，缺点就是参数选的不好就....

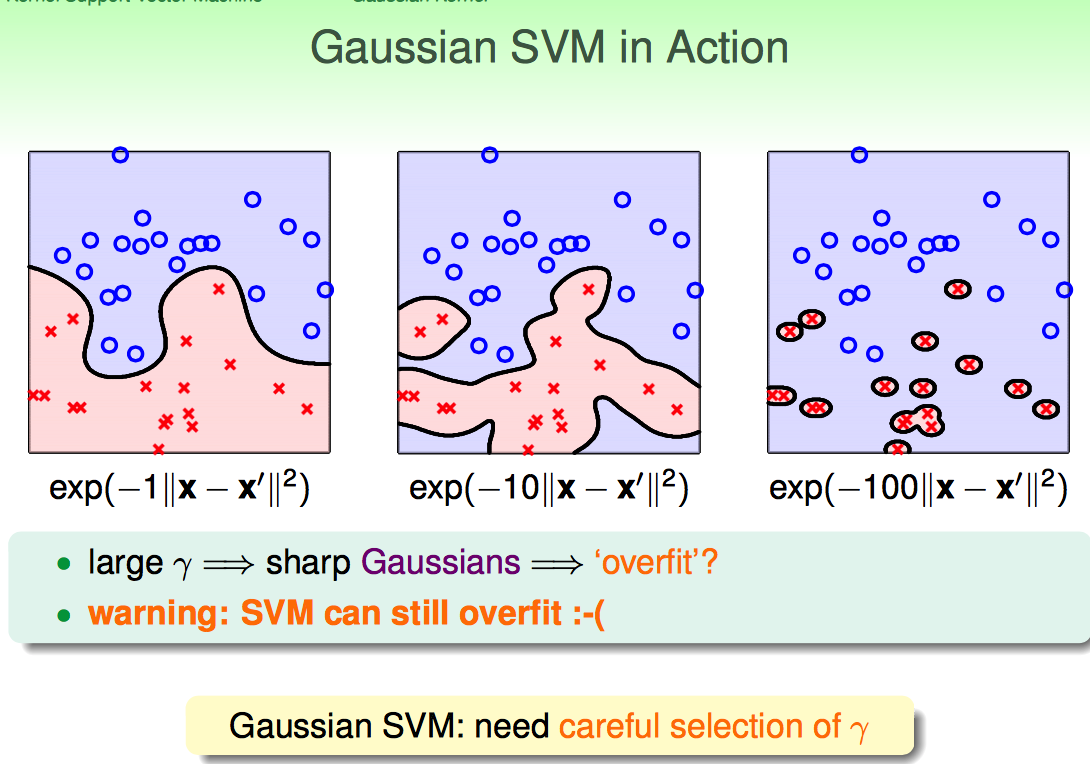
即使是SVM 过拟合依然会出现，要慎用Gaussian SVM。

几种Kernel各有好处，但原则还是要慎用，能用简单的不用复杂的。