数学基础-3D空间的位置表示

转自：http://www.cnblogs.com/gaoxiang12/p/5113334.html

刚体运动

本篇讨论一个很基础的问题：如何描述机器人的位姿。这也是SLAM研究的一个很基本的问题。这里的位姿表示了位置和姿态。描述位置很简单，如果机器人在平面内运动，那么用两个坐标来描述它的位置：

如果在三维空间中运动，则它的位置就用三个空间坐标来表示：

对于姿态来说，在2D情况下还需要增加一个旋转角θ；在3D情况下表达的方式就有多种，常见的如欧拉角、四元素、旋转矩阵等。那么有了位置和姿态，就可以描述一个坐标系；进一步，还能描述坐标系之间的转换关系。常见的问题如：机器人视野中某个点，对世界坐标系的（或地图的）哪个点？这时，就需要先得到该点针对机器人坐标系坐标值，再根据机器人位姿转换到世界坐标系中。

齐次坐标系

在位姿转换中，通常采用射影空间的齐次坐标表示。齐次坐标是什么呢？记n维射影空间为其中一个空间点的坐标为普通的3D坐标加一个齐次分量：

例如，在2维和3维射影空间中的点，分别表示为：

用四个数来表示点，说明点和坐标肯定不是一一对应的。没错，在齐次坐标中，某个点x的分量同乘一个非零常数k后，仍然表示的是同一个点。因此，一个点的具体坐标值不是唯一的。如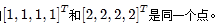但是在w不等于0，可以对每一个坐标除以最后一项w，强制最后一项为1，从而得到一个点唯一的坐标表示：

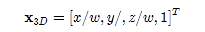
那么为什么要使用齐次坐标来表示呢？原因如下：

1）齐次坐标下点和直线（高维空间里为超平面）能够使用同样的表达。

把点和超平面采用同样的表示，这种做法一个非常直接的好处，是射影几何里的“对偶原理”。该原理是说，任何有关“点”与“平面”的命题，都可以交换“点”与“平面”的概念，得到一个对偶的命题。对偶命题和原命题是一样的。通过“对偶原理”，射影几何的数学家就可以偷懒，只需要证一半定理，因为对偶命题和原命题有同样的涵义。例如，我们证明了 中某条件下三点共线，那么替换概念后的三线共点则自然成立。

2）齐次坐标能囊括无穷远点与无穷远超平面

θθ3）齐次坐标可以方便地将平移与旋转放在一个矩阵中

有关坐标系怎么用齐次坐标进行变换，后文会详细解释。现在我们能表达点了，还剩下一个姿态。由于2D与3D差别较大，我们分而述之。

2D姿态的描述

3D变换

3D的旋转可以由旋转矩阵、欧拉角、四元素等若干种方式描述，它 们也统称为三维旋转群SO(3);而3D的变换即旋转加上位移，是SE(3)。为了和2D变换统一起见，我们首先介绍旋转矩阵表示法。

旋转矩阵描述