codeforces 755D. PolandBall and Polygon

D. PolandBall and Polygon

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

PolandBall has such a convex polygon with n veritces that no three of its diagonals intersect at the same point. PolandBall decided to improve it and draw some red segments.

He chose a number k such that gcd(n, k) = 1. Vertices of the polygon are numbered from 1 to n in a clockwise way. PolandBall repeats the following process n times, starting from the vertex 1:

Assume you've ended last operation in vertex x (consider x = 1 if it is the first operation). Draw a new segment from vertex x to k-th next vertex in clockwise direction. This is a vertexx + k or x + k - n depending on which of these is a valid index of polygon's vertex.

Your task is to calculate number of polygon's sections after each drawing. A section is a clear area inside the polygon bounded with drawn diagonals or the polygon's sides.

Input

There are only two numbers in the input: n and k (5 ≤ n ≤ 106, 2 ≤ k ≤ n - 2, gcd(n, k) = 1).

Output

You should print n values separated by spaces. The i-th value should represent number of polygon's sections after drawing first i lines.

Examples

input

5 2

output

2 3 5 8 11 

input

10 3

output

2 3 4 6 9 12 16 21 26 31 

Note

The greatest common divisor (gcd) of two integers a and b is the largest positive integer that divides both a and b without a remainder.

For the first sample testcase, you should output "2 3 5 8 11". Pictures below correspond to situations after drawing lines.

---

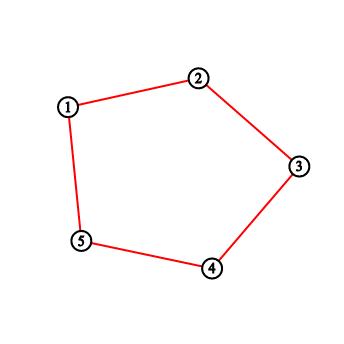
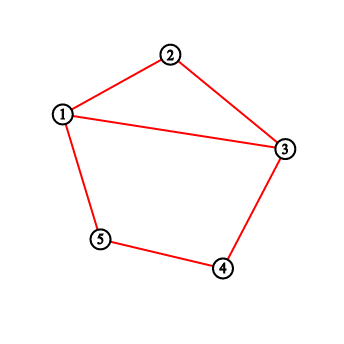
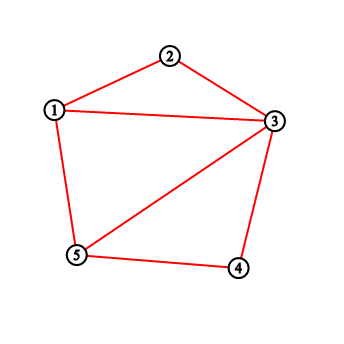
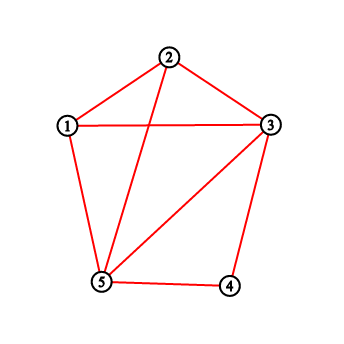
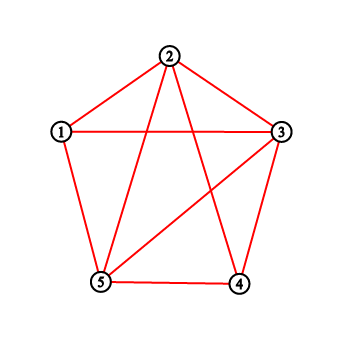
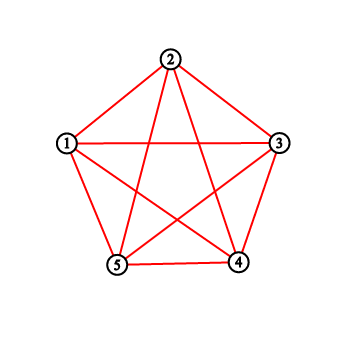
题目大意：一个n边形，从1号点开始，每次走到(x+k-1)%n+1位置，问每次留下来的路径把这个多边形划分成了几个部分。2 ≤ k ≤ n - 2, gcd(n, k) = 1，可以发现一定每个点一定经过一次，插入边的时候对应的点对应了一个区间，两条直线不相交(贡献答案）当且仅当他们的区间无交集，因为一个点只对应一个区间(只考虑出去的那个)，用树状数组维护一下即可。

有个细节：如果2k>n，那么把k转化一下为n-k就可以了。(以为这个细节很显然，然后就没去hack,结果本来房间里10个对的然后就只剩3个没fst，MDZZ)

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<cstdlib>
 #include<cmath>
 #include<cstring>
 using namespace std;
 #define maxn 1000010
 #define llg long long
 #define yyj(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
 llg n,m,cs[maxn],k,x,y,ans,c[maxn];

 llg lowbit(llg x) {return x&-x;}
 void add(llg w,llg v)
 {
     while (w<=n)
     {
         c[w]+=v; w+=lowbit(w);
     }
 }
 llg sum(llg w)
 {
     llg ans=;
     while (w>)
         {
             ans+=c[w]; w-=lowbit(w);
         }
     return ans;
 }

 llg work(llg x,llg y)
 {

     llg l=y,r=y+n-k-k;
     if (r>n)
     {
         r-=n;
         return sum(n)-sum(l-)+sum(r);
     }
     else return sum(r)-sum(l-);
 }

 int main()
 {
     yyj("D");
     cin>>n>>k;
     if (k>n/) k=n-k;
     x=;
     ans=;// add(1,1);
     for (llg i=;i<=n;i++)
     {
         y=x+k;
         if (y>n) y-=n;
         ans+=i-work(x,y);
         add(x,);
         x=y;
         printf("%lld ",ans);
     }
     return ;
 }