【Coursera】基于朴素贝叶斯的中文多分类器

一、算法说明

为了便于计算类条件概率$P(x|c)$,朴素贝叶斯算法作了一个关键的假设：对已知类别，假设所有属性相互独立。
当使用训练完的特征向量对新样本进行测试时，由于概率是多个很小的相乘所得，可能会出现下溢出，故对乘积取自然对数解决这个问题。
在大多数朴素贝叶斯分类器中计算特征向量时采用的都是词集模型，即将每个词的出现与否作为一个特征。而在该分类器中采用的是词袋模型，即文档中每个词汇的出现次数作为一个特征。
当新样本中有某个词在原训练词中没有出现过，会使得概率为0，故使用拉普拉斯平滑处理技术解决这一问题。对应公式如下：

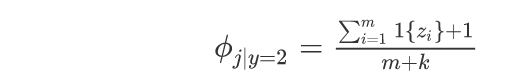
二、数据源

在该模型中，所用到的训练数据和测试数据均来自于搜狗分类语料库，并选择了体育类、财经类和教育类这三种新闻的各40个样本，以作为该多分类器的输入数据。

三、中文分词

为了对文本完成分词，对于英文文本而言，只需要简单得利用str.split(" ")，用空格对整个英文文本进行切割即可。而对于中文文本而言就相对复杂了点，因为在中文文本中，往往包含了中文、英文、数字、标点符号等多种字符，此外中文中常常是多个词组连接起来组成一个句子，所以也无法类似英文那样简单利用某个符号进行分割。为了完成中文文本的分词，使用了如下的文本过滤算法：

stopWords = open("stop_words.txt", encoding='UTF-8').read().split("\n")

def textParse(inputData):

    import re

    global stopWords

    inputData = "".join(re.findall(u'[\u4e00-\u9fa5]+', inputData))

    wordList = "/".join(jieba.cut(inputData))

    listOfTokens = wordList.split("/")

    return [tok for tok in listOfTokens if (tok not in stopWords and len(tok) >= 2)]

利用正则表达式u'[\u4e00-\u9fa5]+'过滤掉输入数据中的所有非中文字符；
在Python下，有个中文分词组件叫做jieba，可以很好得完成对中文文本的分词。在这里便是利用jieba中的cut函数"/".join(jieba.cut(inputData))完成对中文的分词，并且以“/”作为分隔符。
在中文文本中，存在在大量的停用词，这些停用词对于表示一个类别的特征没有多少贡献，因此必需过滤掉输入数据中的停用词。这里所用到的stop_words.txt ,包含了1598个停用词，利用tok not in stopWords过滤掉输入数据中的停用词。
在利用jieba完成分词后，往往会存在大量长度为1的词（不在停用词表里），这些词对特征表示同样贡献不大，利用len(tok) >= 2将其过滤掉。

通过以上过程，便完成了中文文本的分词。分词结果如下：

四、分类结果

为了对分类器的泛化误差进行评估，遂使用留存交叉验证法，即从输入的40 * 3共120个样本中，随机选中20个样本作为测试数据，其他100个样本作为训练数据，以此来测定泛化误差。

经过10次测试，得到分类器的泛化误差为：（0.1 + 0.0 + 0.1 + 0.1 = 0.0 + 0.05 + 0.1 + 0.15 + 0.1 + 0.25）/ 10 = 0.095，可见该中分多分类器在新样本上的表现还是很好的。其中部分分类结果如下所示：