【平面图最小割】BZOJ1001- [BeiJing2006]狼抓兔子

【题目大意】
左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的。开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，如果一条道路上最多通过的兔子数为K，需要同样数量的K只狼伏击，求封锁道路的最小狼数。

【思路】
显然这是最小割，但是最小割效率太低。可以发现这是一张平面图，根据平面图的性质，平面图最小割=对偶图的最短路。所谓对偶图，简单理解就是把面转为点，然后将面之间的边作为连接两个点的边。本题中建立的对偶图如下：

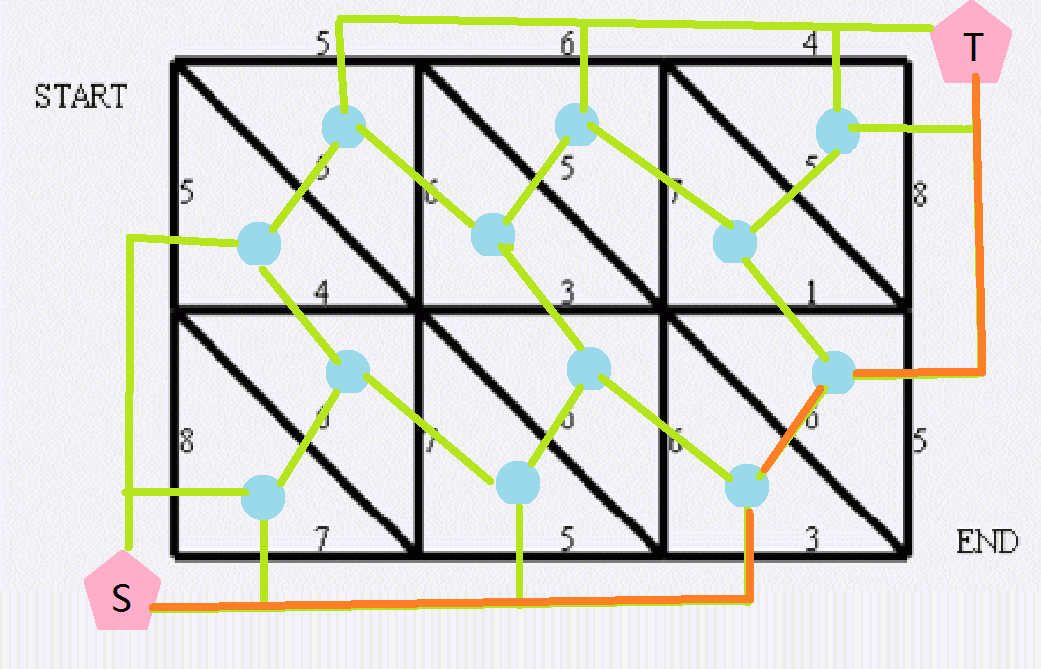
显然可以发现，最短路必然是最小割。

【错误点】
注意一下面转点后，对偶图点的数量和原来点的数量不一样，大概为2倍，数组要开足够大，否则RE！

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 #include<queue>
 #include <utility>
 #define S 0
 #define T 2*(m-1)*(n-1)+1
 using namespace std;
 const int MAXN=;
 const int INF=0x7fffffff;
 struct edge
 {
     int fr,to,len;
 };
 int n,m,w;
 vector<edge> E[MAXN];

 void addedge(int u,int v,int w)
 {
     //cout<<"!"<<u<<' '<<v<<' '<<w<<endl;
     E[u].push_back((edge){u,v,w});
     E[v].push_back((edge){v,u,w});
 }

 int dijkstra()
 {
     priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > que;
     int dis[MAXN],vis[MAXN];
     memset(vis,,sizeof(vis));
     for (int i=S+;i<=T;i++) dis[i]=INF;
     dis[S]=;
     que.push(make_pair<int,int>(,S));
     while (!que.empty())
     {
         int head=que.top().second;que.pop();
         if (!vis[head])
         {
             vis[head]=;
             for (int i=;i<E[head].size();i++)
             {
                 edge Edge=E[head][i];
                 if (!vis[Edge.to] && dis[Edge.to]>dis[Edge.fr]+Edge.len)
                 {
                     dis[Edge.to]=dis[Edge.fr]+Edge.len;
                     que.push(make_pair<int,int>(dis[Edge.to],Edge.to));
                 }
             }
         }
     }
     return (dis[T]);
 }

 void init()
 {
     for (int i=;i<n;i++)
         for (int j=;j<m-;j++)
         {
             scanf("%d",&w);
             if (i==) addedge(*(j+),T,w);
                 else if (i==n-) addedge(S,(n-)*(m-)*+*j+,w);
                     else addedge((i-)*(m-)*+*j+,i*(m-)*+*j+,w);
         }
     for (int i=;i<n-;i++)
         for (int j=;j<m;j++)
         {
             scanf("%d",&w);
             if (j==) addedge(S,i**(m-)+,w);
                 else if (j==m-) addedge((i+)**(m-),T,w);
                     else addedge(i**(m-)+j*,i**(m-)+*j+,w);
         }
     for (int i=;i<(n-);i++)
         for (int j=;j<(m-);j++)
         {
             scanf("%d",&w);
             //cout<<i<<' '<<j<<' ';
             addedge(i**(m-)+*j+,i**(m-)+*j+,w);
         }
 }

 int main()
 {
     scanf("%d%d",&n,&m);
     if (n== && m==) cout<<<<endl;
         else
         {
             init();
             cout<<dijkstra()<<endl;
         }
     return ;
 }