uoj259 & 独立集问题的一些做法
很早以前就做了一遍这题,当时好像啥都不会,今天重做一下。
这个题题意简单地说就是输入k、p和一个图,求图大小为k的独立集个数mod p。
subset1.in n=24,m=19,k=8
subset2.in n=40,m=55,k=11
subset3.in n=100,m=99,k=32
n比较小,直接状压dp即可,细节详见集训队论文(懒得写了),跑得飞快。
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}
#define SZ 666666
int n,m,k,p,cnt=0;
#include <unordered_map>
struct cn
{
ll f[33];
cn() {memset(f,0,sizeof f);}
ll& operator [] (unsigned p) {return f[p];}
};
cn operator + (cn a,cn b)
{
for(int i=1;i<=k;i++)
a[i]=(a[i]+b[i])%p;
return a;
}
cn operator * (cn a,cn b)
{
cn t=a+b;
for(int i=1;i<=k;i++)
for(int j=1;j<=k;j++)
if(i+j<=k)
t[i+j]=(t[i+j]+a[i]*b[j])%p;
return t;
}
cn add1(cn a)
{
cn t; t[1]=1;
for(int i=1;i<k;i++)
t[i+1]=a[i];
return t;
}
unordered_map<bitset<203>,cn> F;
bitset<203> goo[233];
int d[233],ts[233],ff[233];
inline int gf(int x) {return ff[x]?ff[x]=gf(ff[x]):x;}
cn f(bitset<203> r)
{
if(F.count(r)) return F[r];
int p=r.count();
if(!p) return F[r]=cn();
int tn=0,cp=0; cn&g=F[r];
for(int i=1;i<=n;i++)
if(r[i]) ts[++tn]=i,ff[tn]=0,d[tn]=3;
for(int i=1;i<=tn;i++)
for(int j=1;j<=tn;j++)
{
if(goo[ts[i]][ts[j]]) continue;
++d[i]; int ga=gf(i),gb=gf(j);
if(ga!=gb) ff[ga]=gb;
}
for(int i=1;i<=tn;i++)
if(gf(i)==i) ++cp;
if(cp>1)
{
bitset<203>*rs=(bitset<203>*)malloc(sizeof(bitset<203>)*(tn+2));
for(int i=1;i<=tn;i++) rs[i].reset();
for(int i=1;i<=tn;i++)
rs[gf(i)][ts[i]]=1;
cn ans;
for(int i=1;i<=tn;i++)
if(rs[i].count()) ans=ans*f(rs[i]);
return g=ans;
}
int s=1;
for(int i=1;i<=tn;i++) if(d[i]>d[s]) s=i;
s=ts[s]; r[s]=0; cn f1=f(r);
r&=goo[s]; cn f2=add1(f(r));
return g=f1+f2;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&k,&p);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) goo[i][j]=1;
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
goo[a][b]=goo[b][a]=0;
}
bitset<203> all;
for(int i=1;i<=n;i++) all[i]=1;
cn ans=f(all); cout<<ans[k]<<"\n";
}
subset4.in n=100000,m=99999,k=20358
100000 99999 20358 999999937
1 2
1 3
2 4
1 5
4 6
6 7
6 8
6 9
2 10
8 11
4 12
2 13
8 14
10 15
11 16
10 17
...
树?树上大小为k的独立集数量?直接树形dp大概就行了。
记f[i][0/1][j]为包含/不包含i,i子树中,大小为j的独立集数量。暴力转移复杂度大概是平方。
跑了好久好久跑出来了...可能有5min。如果把暴力卷积改成fft(由于数据随机)应该会快一点。
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}
#define SZ 666666
int n,m,k,P,sz[SZ],cnt=0; Edg
vector<int> vs[100003][2];
void dfs(int x)
{
cerr<<++cnt<<"\r";
vs[x][0].resize(2);
vs[x][1].resize(2);
int cs=1; vs[x][0][0]=vs[x][1][1]=1;
for esb(x,e,g)
{
dfs(g);
{
vector<int> tmp,&v1=vs[x][1],&v2=vs[g][0];
tmp.resize(cs+sz[g]+1);
for(int a=0;a<=cs;a++)
for(int b=0;b<=sz[g];b++)
tmp[a+b]=(tmp[a+b]+(ll)v1[a]*v2[b])%P;
v1=tmp;
}
{
vector<int> tmp,&v1=vs[x][0],&v2=vs[g][0],&v3=vs[g][1];
tmp.resize(cs+sz[g]+1);
for(int a=0;a<=cs;a++)
for(int b=0;b<=sz[g];b++)
tmp[a+b]=(tmp[a+b]+(ll)v1[a]*(v2[b]+v3[b]))%P;
v1=tmp; v2.clear(); v3.clear();
}
cs+=sz[g];
}
sz[x]=cs;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&k,&P);
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
ad_de(a,b);
}
dfs(1);
ll ans=vs[1][0][k]+vs[1][1][k];
ans=(ans%P+P)%P; cout<<ans<<"\n";
}
subset5.in n=144,m=264,k=20
看起来奥妙重重。
144 264 20 998244353
1 2
1 13
2 3
2 14
3 4
3 15
4 5
4 16
5 6
5 17
6 7
6 18
7 8
7 19
8 9
8 20
9 10
9 21
10 11
画个图好了...
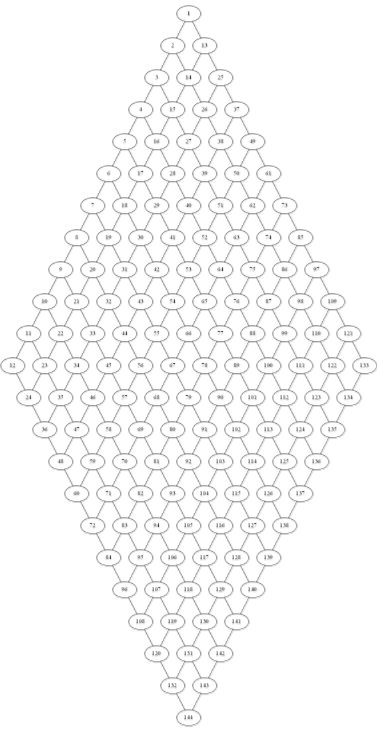
我们发现这是一张十分美观的12*12的网格图,大力状压dp一波好了。
我们直接用f[i][j][k]表示前i行,第i行选的独立集状压之后是j,前i行一共选的大小为k,直接dp即可。
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}
#define SZ 666666
int K,P,c1[SZ];
bool valid[SZ];
int f[2][4444][22];
int main()
{
scanf("%*d%*d%d%d",&K,&P);
int n=12;
for(int i=0;i<(1<<n);i++)
{
valid[i]=1;
for(int j=0;j+1<n;j++)
{
if((i&(1<<j))&&(i&(1<<(j+1))))
valid[i]=0;
}
for(int j=0;j<n;j++) c1[i]+=bool(i&(1<<j));
}
f[0][0][0]=1;
int ans=0;
for(int i=1;i<=n;i++)
{
cerr<<i<<"!!\n"; ans=0;
memset(f[i&1],0,sizeof f[0]);
auto &c=f[i&1],&p=f[(i&1)^1];
for(int j=0;j<(1<<n);j++)
{
if(!valid[j]) continue;
for(int k=0;k<(1<<n);k++)
{
if(!valid[k]||(j&k)) continue;
for(int g=c1[j];g<=K;g++)
c[j][g]=(c[j][g]+p[k][g-c1[j]])%P;
}
ans=(ans+c[j][K])%P;
}
}
cout<<ans<<"\n";
}
subset6.in n=500,m=5000,k=55
看起来非常奥妙重重,但是这个图有点大,我并不能画出来。
我猜这是一个k仙人图!测了测,一条树边至多被...2098条边覆盖?好僵硬啊
看了看度数,感觉非常正态分布?这个点不会是随机的吧...
既然这个点能做,那么肯定有特殊性质...我猜这是一个分层图!
那么问题来了,怎么把一个分层图分层...
一种简单的做法是bfs这个图,那么同一层的bfs序上比较容易挨在一起。
我们定义od[i]为i的新编号,同一层的编号挨在一起。
假设每层点数一样,因为一条边不是层内的就是跨层的,所以每层点数只要定为max(|od[a]-od[b]|)(a、b是某条边的端点)上取整即可。
按输入顺序连完边好像max(|od[a]-od[b]|)大概是40,太大了。多shuffle几次边跑了一会儿跑出来一个max(|od[a]-od[b]|)=30的解,那么每层可以30个点。
我们还是用f[i][j][k]表示前i层,第i行选的独立集状压之后是j,前i行一共选的大小为k。
直接dp复杂度似乎复杂度妥妥爆炸,但是因为这个图比较密,所以每一层合法的独立集没有这么多,所以实际上还是能跑出来的,跑得还挺快的。
调了一年:
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}
#define SZ 666666
Edgc
bool edg[2333][2333];
int n,m,K,p,ea[SZ],eb[SZ],od[SZ],to[SZ];
void bfs(int x)
{
static int qs[SZ];
static bool vis[SZ];
for(int i=0;i<n;i++) vis[i]=0;
int h=0,t=0,C=0; qs[t++]=x;vis[x]=1;
while(h^t)
{
int x=qs[h++]; od[x]=C++;
for esb(x,e,b)
{
if(vis[b]) continue;
vis[b]=1; qs[t++]=b;
}
}
}
int vi[SZ];
pii ps[SZ];
vector<int> sta[233];
ll f[2][65537][56];
typedef bitset<32> bs;
vector<int>*tv; int off,nn;
void dfs(int st,int cur,bs x)
{
tv->pb(cur);
for(int g=x._Find_next(st);g<nn;g=x._Find_next(g))
{
bs nx=x;
for(int j=0;j<nn;j++)
if(edg[off+g][off+j]) nx[j]=0;
dfs(g,cur|(1<<g),nx);
}
}
int main()
{
srand(19260817); //如何让程序跑得飞快
scanf("%d%d%d%d",&n,&m,&K,&p);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&ps[i].fi,&ps[i].se);
--ps[i].fi,--ps[i].se;
}
int minn=1e9;
while(1)
{
for(int i=0;i<n;i++) fst[i]=0; M=0;
random_shuffle(ps+1,ps+1+m);
for(int i=1;i<=m;i++)
{
ea[i]=ps[i].fi;eb[i]=ps[i].se;
adde(ea[i],eb[i],i);
}
bfs(0); int qw=0;
for(int i=1;i<=m;i++)
qw=max(qw,abs(od[eb[i]]-od[ea[i]]));
if(minn<=31)
{
cerr<<"good\n";
break;
}
if(qw>=minn) continue; minn=qw;
for(int i=0;i<n;i++) to[i]=od[i];
cerr<<qw<<"\n";
}
for(int i=0;i<n;i++) od[i]=to[i];
int P=minn,c=0;
for(int i=1;i<=m;i++)
edg[od[ps[i].fi]][od[ps[i].se]]=
edg[od[ps[i].se]][od[ps[i].fi]]=1;
for(int i=0;i*P<n;i++)
{
++c; int s=min(n-i*P,P);
bs p; for(int i=0;i<s;i++) p[i]=1;
tv=&sta[c]; off=i*P; nn=s; dfs(-1,0,p);
}
f[1][0][0]=1; sta[0].pb(0);
static int x[233],y[233];
for(int i=0;i<c;i++)
{
cerr<<"layer"<<i<<"/"<<c<<" "<<sta[i+1].size()<<"\n";
memset(f[i&1],0,sizeof f[0]);
ll ans=0;
for(int ij=0;ij<sta[i+1].size();ij++)
{
int j=sta[i+1][ij];
for(int g=0;g<=K;g++)
f[i&1][ij][g]=0;
for(int ik=0;ik<sta[i].size();ik++)
{
int k=sta[i][ik];
int xn=0,yn=0;
for(int a=0;a<P;a++)
if(j&(1<<a)) x[++xn]=a;
for(int a=0;a<P;a++)
if(k&(1<<a)) y[++yn]=a;
for(int _=1;_<=xn;_++)
{
for(int __=1;__<=yn;__++)
{
int a=x[_],b=y[__];
if(edg[a+i*P][b+i*P-P])
goto gg2;
}
}
//cont. xn
for(int g=xn;g<=K;g++)
f[i&1][ij][g]=(f[i&1][ij][g]+f[!(i&1)][ik][g-xn])%p;
gg2:;
}
ans=(ans+f[i&1][ij][K])%p;
}
if(i==c-1) printf("%lld\n",ans);
}
}
subset7.in n=4998,m=5002,k=666
subset8.in n=11986,m=12011,k=1098
这两个点的共同点是m≈n,m-n不大,连通图。
这种图可以通过dfs树+覆盖边状压dp解决,就状压覆盖父亲边的非树边的顶端的选择情况。
细节不清楚的看集训队论文吧...写起来着实感人。
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}
#define SZ 666666
Edg
int n,m,dfn[SZ],C=0,dep[SZ],fa[SZ],fc[SZ];
bool vis[SZ];
void dfs(int x)
{
dfn[x]=++C; vis[x]=1;
for esb(x,e,b)
if(!vis[b]) dep[b]=dep[x]+1,fa[b]=x,dfs(b);
}
int ea[SZ],eb[SZ],K,P,ys[23333333];bool te[SZ];
vi cv[SZ];
//use array ys to for binary ones in x.
#define forb(x,y) for(int x##__temp__=x,y;x##__temp__&&(y=ys[x##__temp__&(-x##__temp__)])+1;x##__temp__-=1<<y)
//-Wl,--stack=23333333 might be needed.
struct Arr{int g[1100];
Arr() {for(int i=0;i<=K;i++) g[i]=0;}
inline int& operator[] (int x) {return g[x];}
const Arr& operator = (const Arr&b)
{for(int i=0;i<=K;i++) g[i]=b.g[i];}};
vector<Arr> F[12000],G[12000];
Arr operator + (Arr a,Arr b)
{
Arr p;
for(int i=0;i<=K;i++) p[i]=(a[i]+b[i])%P;
return p;
}
Arr operator * (Arr a,Arr b)
{
Arr p;
for(int i=0;i<=K;i++)
{
if(!a[i]) continue;
for(int j=0;i+j<=K;j++)
{
if(!b[j]) continue;
p[i+j]=(p[i+j]+(ll)a[i]*b[j])%P;
}
}
return p;
}
bool ins[SZ];
int cnt=0,tot=0;
void dp(int x)
{
vector<int> son;
for esb(x,e,b)
{
if(fa[b]!=x) continue;
dp(b); son.pb(b);
}
vector<Arr> lf,cf,lg,cg,em;
vector<bool> valg;
int S=1<<cv[x].size();
cout<<(cnt+=S)/(double)tot<<"\r";
valg.resize(S);
for(int j=0;j<S;j++)
{
forb(j,g)
if(eb[cv[x][g]]==x) goto not_valid_QAQ;
valg[j]=1; not_valid_QAQ:;
}
em.resize(S); lf=cf=lg=cg=em;
for(int j=0;j<(1<<cv[x].size());j++)
{
cf[j][0]=1;
if(valg[j]) cg[j][1]=1;
}
for(auto s:son)
{
lf=cf; lg=cg; cf=cg=em;
//cons. f
for(int j=0;j<(1<<cv[x].size());j++)
{
forb(j,g) ins[ea[cv[x][g]]]=1;
{
int su=0;
for(int k=0;k<cv[s].size();k++)
if(ins[ea[cv[s][k]]]) su|=1<<k;
cf[j]=lf[j]*(F[s][su]+G[s][su]);
}
if(valg[j])
{
ins[x]=1;
int su=0;
for(int k=0;k<cv[s].size();k++)
if(ins[ea[cv[s][k]]]) su|=1<<k;
cg[j]=lg[j]*F[s][su];
ins[x]=0;
}
forb(j,g) ins[ea[cv[x][g]]]=0;
}
F[s].clear(); G[s].clear();
}
F[x]=cf; G[x]=cg;
}
int main()
{
for(int i=0;(1<<i)<23333333;++i) ys[1<<i]=i;
srand(19260817);
scanf("%d%d%d%d",&n,&m,&K,&P);
for(int i=1;i<=m;i++)
{
scanf("%d%d",ea+i,eb+i),
adde(ea[i],eb[i]);
if(ea[i]==eb[i]) throw "WTF";
}
cerr<<"Finding Root\n";
ll minn=1e18; int g;
for(int p=1;p<=n;p++)
{
C=0;
for(int i=1;i<=n;i++) fc[i]=vis[i]=fa[i]=0;
dep[p]=1; dfs(p);
for(int i=1;i<=m;i++)
{
if(fa[ea[i]]==eb[i]||fa[eb[i]]==ea[i]);
else
{
int a=ea[i],b=eb[i];
if(dep[a]>dep[b]) swap(a,b);
//a is an ancestor of b
for(int j=b;j!=a;j=fa[j]) ++fc[j];
}
}
ll s=0;
for(int i=1;i<=n;i++) s+=1LL<<fc[i];
if(s<minn) minn=s,g=p;
}
cerr<<"PRE2\n";
C=0; tot=minn;
for(int i=1;i<=n;i++) fc[i]=vis[i]=fa[i]=0;
dep[g]=1; dfs(g);
for(int i=1;i<=m;i++)
{
if(dep[ea[i]]>dep[eb[i]]) swap(ea[i],eb[i]);
//ea[i] is lower than eb[i]
if(fa[eb[i]]==ea[i]) te[i]=1;
else
{
int a=ea[i],b=eb[i];
for(int j=b;j!=a;j=fa[j]) cv[j].pb(i);
}
}
cerr<<"READY\n";
dp(g);
ll p=((F[g][0][K]+G[g][0][K])%P+P)%P;
cout<<"\n\n\n\n"<<p<<"\n";
}
subset9.in n=32748,m=196467,k=3360。
1 2
1 3
1 4
5 1
1 6
7 1
...
14369 14372
14373 14369
14369 14374
14369 14375
14370 14371
14372 14370
14373 14370
14374 14370
14370 14375
14370 14376
...
这个点的特点是连边的两端点编号差值都不大,直接状压dp即可。
subset10.in n=64319,m=200000,k=10373。
这个点看起来非常随机!看起来十分感人。
我们来统计一下每个点的度数...怎么全在8以内?还有这种操作?
咦这个点放在9号点后面肯定别有用心,我猜这个点重编号之后连边的两端点编号差值也都不大!
那么我们现在就是要把点重编号,使得图的bandwidth尽量小。
求尽量小的bandwidth有一个Cuthill-Mckee Algorithm,算法大致如下:
这是一种广义的bfs,我们一开始先选定最小度数的点作为起点,给起点标1号,然后每次扩展一圈(和上次扩展的点相邻的点),然后按度数排序并编号。
用这个算法求出的bandwidth为16。
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}
#define SZ 666666
//Try Cuthill-McKee Algorithm
Edg
bool vis[SZ];
int n,m,k,P,d[SZ],od[SZ],ea[SZ],eb[SZ];
vector<vi> r;
bool by_d(int a,int b) {return d[a]<d[b];}
int f[2][129][3456];
int main()
{
scanf("%d%d%d%d",&n,&m,&k,&P);
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
adde(a,b);
++d[a];++d[b];
ea[i]=a,eb[i]=b;
}
d[0]=1e9; int md=0;
for(int i=1;i<=n;i++)
if(d[i]<d[md]) md=i;
for(int i=1;i<=n;i++)
vis[i]=0;
vis[md]=1; vi tmp; tmp.pb(md);
r.pb(tmp); int s=1;
while(s<n)
{
vi t=r[r.size()-1],tmp;
for(auto x:t)
for esb(x,e,b)
if(!vis[b]) tmp.pb(b),vis[b]=1,++s;
sort(tmp.begin(),tmp.end(),by_d);
r.pb(tmp);
}
int C=0,mx=0;
for(auto s:r)
for(auto p:s)
od[p]=++C;
cout<<n<<" "<<m<<" "<<k<<" "<<P<<"\n";
for(int i=1;i<=m;i++) cout<<od[ea[i]]<<" "<<od[eb[i]]<<"\n";
}
重编号之后就可以dp了,直接dp比较慢,需要注意的是我们可以只存、只dp合法状态,就可以加速了。经过一些wys,大概要跑20min左右。
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])
#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}
#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}
#define SZ 666666
int n,m,fb[SZ],K,p;
int f[2][5555][11000],bk[131088];
vector<int> goo[12345];
int main()
{
scanf("%d%d%d%d",&n,&m,&K,&p);
int S=0,mx=0;
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
if(a>b) swap(a,b);
//a<=b
fb[b]|=1<<(b-a);
S=max(S,1<<(b-a+1));
}
cerr<<S<<" "<<K<<"GG\n";
f[0][0][0]=1; goo[0].pb(0);
int pv=0,st=clock();
for(int i=1;i<=n;i++)
{
vi&ti=goo[i&1],&pi=goo[!(i&1)];
ti.clear();
for(int _=0;_<pi.size();_++)
{
int j=pi[_];
for(int k=0;k<=K;k++)
if(f[!(i&1)][_][k]) goto good_;
continue;
good_:
ti.pb((j<<1)&(S-1));
if((j<<1)&fb[i]);else
ti.pb(((j<<1)&(S-1))|1);
}
sort(ti.begin(),ti.end());
ti.erase(unique(ti.begin(),ti.end()),ti.end());
mx=max(mx,(int)ti.size());
for(int j=0;j<ti.size();j++)
memset(f[i&1][j],0,sizeof f[0][0]),bk[ti[j]]=j;
for(int _=0;_<pi.size();_++)
{
int j=pi[_];
int*tg=f[i&1][bk[(j<<1)&(S-1)]],
*ss=f[!(i&1)][_];
for(int k=0;k<=K;k+=8)
{
#define par(s) \
tg[k+s]+=ss[k+s]; if(tg[k+s]>=p) tg[k+s]-=p;
par(0) par(1) par(2) par(3)
par(4) par(5) par(6) par(7)
#undef par
}
if((j<<1)&fb[i]) continue;
int*t2=f[i&1][bk[((j<<1)&(S-1))|1]]+1;
for(int k=0;k<=K;k+=8)
{
#define par(s) \
t2[k+s]+=ss[k+s]; if(t2[k+s]>=p) t2[k+s]-=p;
par(0) par(1) par(2) par(3)
par(4) par(5) par(6) par(7)
#undef par
}
}
if(clock()-pv>1000) pv=clock(),
cerr<<i<<" "<<goo[i&1].size()<<" "<<S<<" "<<mx<<"w"<<(n-i)/(ld)i*(clock()-st)/1000.0<<"s rm\n";
}
cerr<<"\n";
ll ans=0;
for(int j=0;j<goo[n&1].size();j++)
ans+=f[n&1][j][K];
ans%=p; cout<<ans<<"\n";
}
这个题好像做了好久啊,完结撒花
uoj259 & 独立集问题的一些做法的更多相关文章
- POJ 3692:Kindergarten 求补图的最大点独立集 头一次接触这样的做法
Kindergarten Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 5884 Accepted: 2877 Desc ...
- 【BZOJ-1952】城市规划 [坑题] 仙人掌DP + 最大点权独立集(改)
1952: [Sdoi2010]城市规划 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 73 Solved: 23[Submit][Status][ ...
- 【BZOJ4316】小C的独立集(仙人掌,动态规划)
[BZOJ4316]小C的独立集(仙人掌,动态规划) 题面 BZOJ 题解 除了普通的动态规划以外,这题还可以用仙人掌的做法来做. 这里没有必要把圆方树给建立出来 \(Tarjan\)的本质其实就是一 ...
- 几个解决k染色问题的指数级做法
几个解决k染色问题的指数级做法 ——以及CF908H题解 给你一张n个点的普通无向图,让你给每个点染上k种颜色中的一种,要求对于每条边,两个端点的颜色不能相同,问你是否存在一种可行方案,或是让你输出一 ...
- 【Luogu】P2774方格取数问题(最大点权独立集)
题目链接 不知道为啥坠大点权独立集的做法跟最大权闭合图差不多? qwq 放个链接 #include<cstdio> #include<cstring> #include< ...
- 9.1.3 .net framework通过业务逻辑层自动生成WebApi的做法
首先需要说明的是这是.net framework的一个组件,而不是针对.net core的.目前工作比较忙,因此.net core的转换正在编写过程中,有了实现会第一时间贴出来. 接下来进入正题.对于 ...
- POJ2104 K-th Number [分块做法]
传送:主席树做法http://www.cnblogs.com/candy99/p/6160704.html 做那倒带修改的主席树时就发现分块可以做,然后就试了试 思想和教主的魔法差不多,只不过那个是求 ...
- 移动端Web适配的两种做法思路总结
看了几篇文章,理一下网易跟淘宝移动端适配的思路,主要是参考 从网易与淘宝的font-size思考前端设计稿与工作流 像素相关概念 物理像素(physical pixel) 一个物理像素是显示器(手机屏 ...
- 一个哥们看到数据库日志不断增大 [log_reuse_wait_desc]为replication 之后的做法
一哥们看到数据库日志不断增大 [log_reuse_wait_desc]为replication 之后的做法 一天那个哥们看到数据库日志暴涨,用sys.databases 视图看一下[log_reus ...
随机推荐
- JUC——线程同步锁(ReentrantReadWriteLock读写锁)
读写锁简介 所谓的读写锁值得是两把锁,在进行数据写入的时候有一个把“写锁”,而在进行数据读取的时候有一把“读锁”. 写锁会实现线程安全同步处理操作,而读锁可以被多个对象读取获取. 读写锁:ReadWr ...
- Siki_Unity_3-3_背包系统
Unity 3-3 背包系统(基于UGUI) 任务1&2&3:演示.介绍.类图分析 背包面板.箱子面板.锻造合成面板.装备佩戴面板.商店面板等 面板的显示和隐藏.保存和加载.拾起物品. ...
- Java SE练习题——求奇数
欢迎来到Java SE练习题频道,我是Fishing,今天我带来的练习题是(做题会有不足之处,可评论,说出更好的方法): 通过键盘输入两个整数,计算这两个整数之间的所有奇数之和,并输出计算结果. 看到 ...
- 简介几种系统调用函数:write、read、open、close、ioctl
在 Linux 中,一切(或几乎一切)都是文件,因此,文件操作在 Linux 中是十分重要的,为此,Linux 系统直接提供了一些函数用于对文件和设备进行访问和控制,这些函数被称为系统调用(sysca ...
- java并发编程原理
一.java内存模型 Java内存模型的主要目标是定义程序中各个变量的访问规则,即在虚拟机中将变量存储到内存和从内存中取出变量这样底层细节.此处的变量与Java编程时所说的变量不一样,指包括了实例字段 ...
- Python20-Day07
面向对象之继承与派生 什么是继承? 继承是一种创建新类的方式,新建的类可以继承一个或者多个父类,父类又称为基类或者超类,新建的类称为派生类或者子类 子类会‘遗传’父类的特性,从而解决代码重用问题 py ...
- First Scrum Meeting (2015/10/18)
会议是在昨晚进行的,本来早就应该写博了,可惜今天校园网炸个不停= =.刚修好就赶紧来发博客. 会议基本要素 会议主题:爬虫项目的核心技术讨论以及项目初期的工作分配 会议时间:2015.10.18 19 ...
- Scrum Meeting 10.22
Scrum Meeting No.2 今天的主要任务是配置安卓开发环境,并运行上一届的项目. 主流的安卓开发环境有eclipse+ADT+SDK和android studio两种.两种环境的文件架构似 ...
- 每天学一点easyui①
引入js和css文件 <script type="text/javascript" src="js/jquery-easyui-1.4.3/jquery.min.j ...
- 第一次spring冲刺第3、4天
11月14至15日 因为忙于项目的谈论与探究,以及周末的活动变动,使得博客没有时间提交上去,这里补交. 这两天,主要是应对于市场的探究做谈论,我们主要面对什么类型的客户,以及他们最需要的是什么等话题做 ...
