科学计算三维可视化---Mayavi入门（Mayavi管线）

一：Mayavi管线

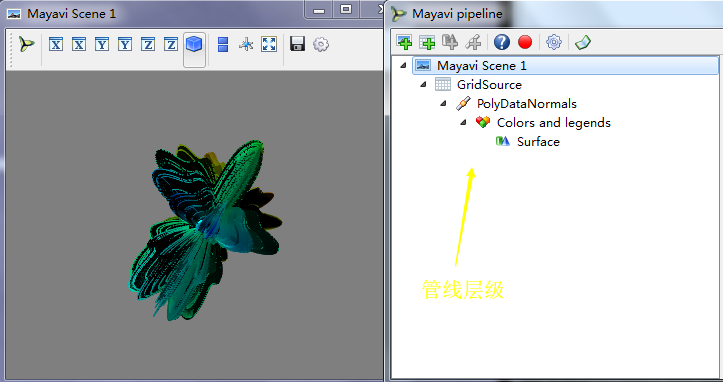
mlab.show_pipeline()　　#显示管线层级，来打开管线对话框

（一）管线中的对象scene

Mayavi Scene:处于树的最顶层的对象，他表示场景，配置界面中可以设置场景的背景，前景色，场景中的灯光，以及其他一些选项

>>> s = mlab.gcf()　　#获取当前场景
>>> print(s)　　#获取当前场景状态
<mayavi.core.scene.Scene object at 0x00000000014E66D0>
>>> print(s.scene.background)　　#输出管线中的背景色
(0.5, 0.5, 0.5)

（二）GridSource网格数据源

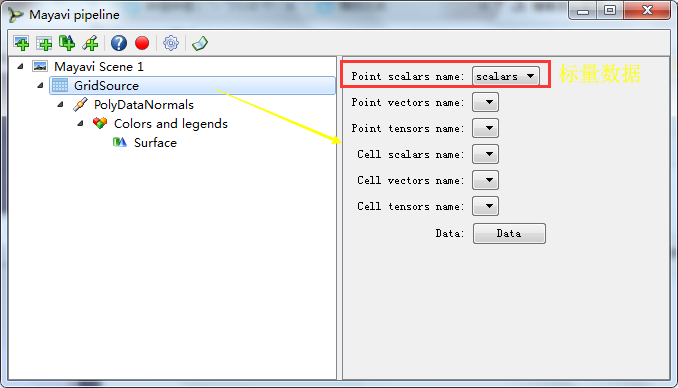
scalars标量数据，他就是传递给mesh的标量数组，他表示mesh表面的每个点的数组

>>> source = s.children[]　　#获取GridSource对象，因为scene场景中有多个数据集合sources,我们获取当前唯一的这一个
>>> print(repr(source))　　#打印返回的字符串
<mayavi.sources.vtk_data_source.VTKDataSource object at 0x0000000014117570>
>>> print(source.name)　　#返回该节点的名称
GridSource

>>> print(repr(source.data.points))　　#打印GridSource的坐标（空间坐标，三维）
[(0.0, 1.0852211291184772, 0.0), ..., (-0.01969313518771439, -1.5671711510166164
, -0.00024748426251406075)], length = 　　#length说明坐标数组大小是126504

>>> print(repr(source.data.point_data.scalars))　　#打印出每个点对应的标量数组
[0.0, ..., -0.00024748426251406075], length = 

（三）PolyDataNormals是数据源的法向量

>>> manager = source.children[]
>>> print(manager)
<mayavi.filters.poly_data_normals.PolyDataNormals object at 0x00000000163D1308>

（四）Colors and legends

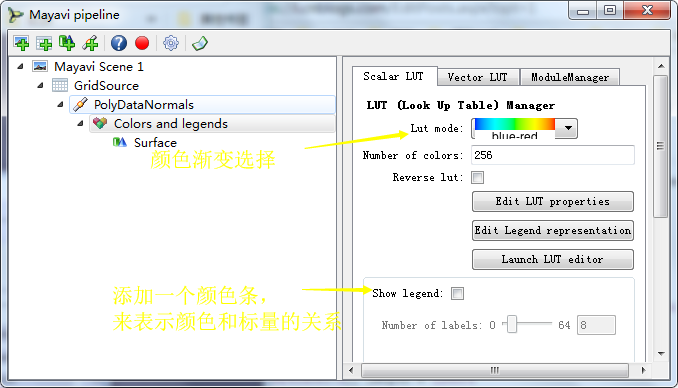
>>> colors = manager.children[]
>>> colors.scalar_lut_manager.lut_mode = "Blues"
>>> colors.scalar_lut_manager.show_legend = True

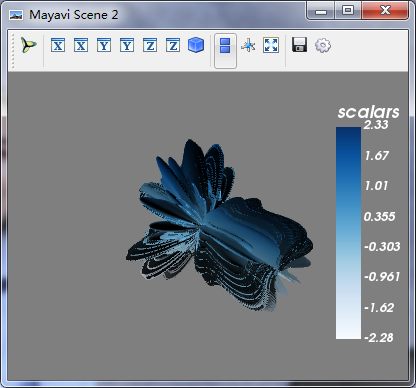
（五）Surface对象：将GridSource输出的PolyData数据转换为最终的在场景中显示的三维实体

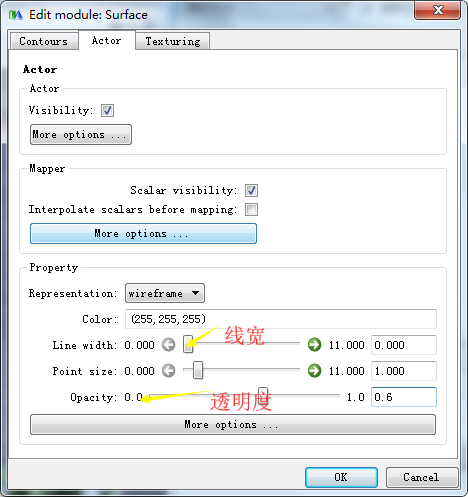
>>> surface = colors.children[]    #获得颜色的第一个子节点
>>> surface.actor.property.representation = "wireframe"
>>> surface.actor.property.opacity = 0.6

总结：程序配置属性的步骤

.获取场景对象，mlab.gcf()
.通过children属性，在管线中找到需要修改的对象
.当其配置窗口由多个选项卡，属性需要一级一级获得

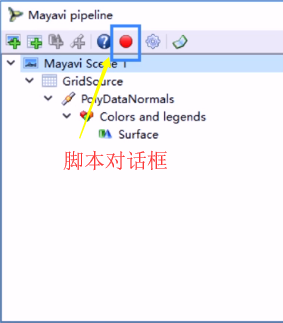
Mayavi管线：是层级管线，相互嵌套，需要使用children获取下一级
TVTK管线：分为可视化管线和图形管线两部分，用于将TVTK中各个对象穿连起来