jubeeeeeat

http://cdqz.openjudge.cn/2016/0003/

总时间限制:

1000ms

内存限制:

256000kB

描述

众所周知，LZF很喜欢打一个叫Jubeat的游戏。这是个音乐游戏，游戏界面是4×4的方阵，会根据音乐节奏要求玩家按下一些指定方块（以下称combo）。LZF觉得这太简单了，于是自己仿了个游戏叫Jubeeeeeat，唯一不同之处就是界面大小，Jubeeeeeat的界面为n×n的方阵。

在某一刻，界面同时出现了若干个combo。LZF终于觉得有些困难了，但毕竟LZF不是普通人，他有很多只手。LZF的手分为m只“肉质手”和q只“意念手”。顾名思义，“肉质手”是实际存在的手，每只肉质手都有5根手指，每根手指能按一个combo，但每只手的速度都不同，受限于此，LZF的每只肉质手的控制范围是一个固定大小的正方形。“意念手”即虚无之手，每只手只有1根手指，但控制范围为全局。

现在LZF想知道，他最多能按下多少个combo。

输入

输入文件名为 jubeeeeeat.in。
第1行输入三个正整数n，m，q。 接下来是一个n×n的01矩阵，描述combo的位置，1为combo。 最后m行每行三个正整数xi，yi，ai，分别表示第i只肉质手掌控区域左上方块的行、列和边长。（行、列从1数起）

输出

输出文件名为 jubeeeeeat.out。 输出一个正整数，表示最多能按下的combo数。

样例输入

3 1 3
1 0 1
1 1 1
1 0 1
1 1 2

样例输出

6

提示

【数据说明】 对于20%的数据，n=5，m=2，q=2； 对于50%的数据，1≤n≤20，1≤m, q≤50； 对于100%的数据，1≤n≤40，1≤m, q≤300，1≤xi, yi≤n，1≤xi+ai-1, yi+ai-1≤n。

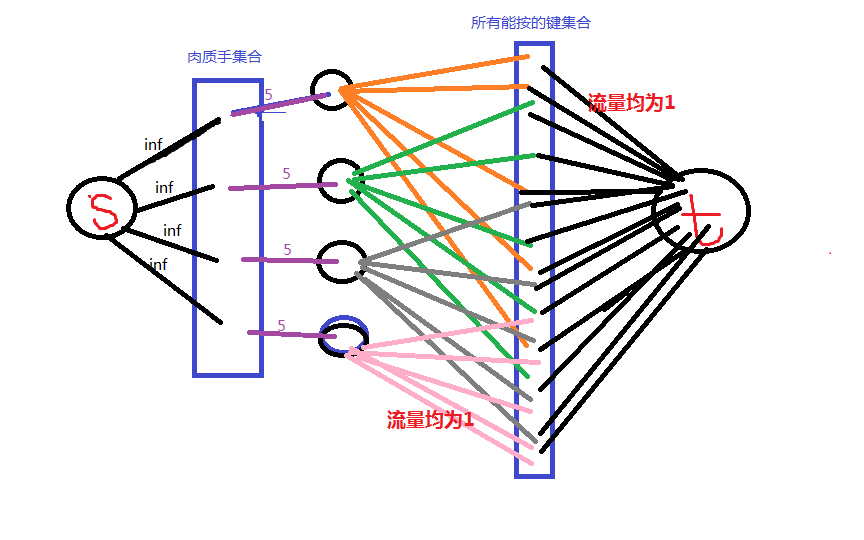
最大流

因为意念手可以控制全局，所以可以不参与构图，最后特殊判断即可

肉质手构图方式

#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#include<iostream>
#define inf 600001
using namespace std;
int n,m,qq,tot=,ans;
int src,decc,key[][];
int front[],cap[],lev[],cnt[],nextt[],to[];
queue<int>q;
void add(int u,int v,int w)
{
    to[++tot]=v;cap[tot]=w;nextt[tot]=front[u];front[u]=tot;
    to[++tot]=u;cap[tot]=;nextt[tot]=front[v];front[v]=tot;
}
bool bfs()
{
    for(int i=;i<=n*n+*m+;i++) {cnt[i]=front[i];lev[i]=-;}
    while(!q.empty()) q.pop();
    q.push(src);lev[src]=;
    while(!q.empty())
    {
        int now=q.front();q.pop();
        for(int i=front[now];i!=;i=nextt[i])
        {
            int t=to[i];
            if(cap[i]>&&lev[t]==-)
            {
                q.push(t);
                lev[t]=lev[now]+;
                if(t==decc) return true;
            }
        }
    }
    return false;
}
int dinic(int now,int flow)
{
    if(now==decc) return flow;
    int delta,rest=;
    for(int & i=cnt[now];i!=;i=nextt[i])
    {
        int t=to[i];
        if(lev[t]==lev[now]+&&cap[i]>)
        {
            delta=dinic(t,min(cap[i],flow-rest));
            if(delta)
            {
                cap[i]-=delta;cap[i^]+=delta;
                rest+=delta;if(rest==flow) break;
            }
        }
    }
    if(rest!=flow) lev[now]=-;
    return rest;
}
int main()
{
   scanf("%d%d%d",&n,&m,&qq);
   for(int i=;i<=n;i++)
    for(int j=;j<=n;j++)
     scanf("%d",&key[i][j]);
    decc=n*n+m*+;
    for(int i=;i<=m;i++) add(src,i,);
    for(int i=;i<=m;i++) add(i,i+m,);
    int x,y,h;
    for(int i=;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&h);
        for(int j=x;j<x+h;j++)
         for(int k=y;k<y+h;k++)
          if(key[j][k])
          add(i+m,(j-)*n+k+*m,);
    }
    for(int i=;i<=n*n;i++)
     add(*m+i,decc,);
    while(bfs())
     ans+=dinic(src,inf);
    ans+=n*n-ans<=qq ? n*n-ans:qq;
    printf("%d",ans);

}