题解：UVa1025 A Spy in the Metro

原题链接

pdf

题目大意

给出一张无向图图，求该图的最小瓶颈生成树。

无向图的瓶颈生成树：无向图\(G\)的一颗瓶颈生成树是这样的一颗生成树：它最大的边权值在\(G\)的所有生成树中是最小的。瓶颈生成树的值为\(T\)中最大权值边的权。

该图建立在坐标系中， 给出每个点的坐标。任意两点之间都有边，边权即为两点间的距离。

题解

由于只关心生成树的最大值，我们可以将边从小到大排序，依次加入（若构成环则不加入），直到构成一颗生成树。

相信你已经发现了：这不就是Kruskal算法吗？

于是，我们得出结论：无向图的最小生成树一定是瓶颈生成树。

如果你仍然感到怀疑，那么我们再用反证法证明：

假设存在一张无向图的最小生成树\(T\)不是瓶颈生成树，那么我们找到该最小生成树的权值最大边\(e\)，我们选取该图中的一颗瓶颈生成树\(T_1\)，则有：对于\(T_1\)中的任何边\(e_1\)，存在\(V_{e_1} <V_{e}\)。删除\(T\)中的\(e\)，我们得到两棵树\(T_a,T_b\)。由于\(T_1\)是一颗生成树，必有一条边\(e_{ab}\)连接\(T_a,T_b\)，用\(e_{ab}\)替换\(e\)，可以得到更小的生成树，与\(T\)是最小生成树矛盾。证毕。

顺便提一句，无向图瓶颈生成树一定是最小生成树吗？

看一看下图就知道了：

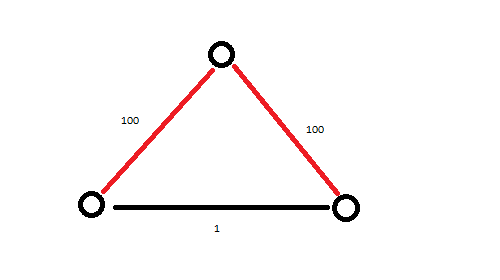
由于本题是稠密图，最好用Prim解决（然而懒到家的我还是用了Kruskal）。

听说有一种复杂度更优的算法叫Camerini's algorithm（然而我并不会），如果有大神会的话也可以教导我一下。

代码

#include <cstdio>
#include <cmath>
#include <algorithm>

using namespace std;

const int maxn = 5005;

struct City
{
	double x, y;//注意是小数（开float似乎也行）
} city[maxn];

struct Edge
{
	int from, to;
	double dist;

	bool operator < (const Edge& other) const
	{
		return dist < other.dist;
	}
} edge[maxn*maxn];

int n, m, S;

inline double sqr(double a)
{
	return a*a;
}

inline double make_dist(City a, City b)
{
	return sqrt(sqr(a.x-b.x) + sqr(a.y-b.y));
}

inline void add_edge(City a, City b, int ai, int bi)
{
	double dist = make_dist(a, b);
	m++;
	edge[m].from = ai;
	edge[m].to = bi;
	edge[m].dist = dist;
}

inline void read()
{
	scanf("%d%d", &S, &n);
	S = n-S;
	for(int i = 1; i <= n; ++i)
	{
		scanf("%lf%lf", &city[i].x, &city[i].y);
		for(int j = 1; j < i; ++j)
			add_edge(city[i], city[j], i, j);
	}
}

struct UN_set
{
	int fa[maxn];

	inline void init(int n)
	{
		for(int i = 1; i <= n; ++i)
			fa[i] = i;
	}

	inline int getfa(int x)
	{
		return fa[x] == x ? x : fa[x] = getfa(fa[x]);
	}
} un;

inline double Kruskal()//其实最好还是用prim
{
	int tmp = 0;
	m = 0;
	read();
	sort(edge+1, edge+m+1);
	un.init(n);
	for(int i = 1; i <= m; ++i)
	{
		int ff = un.getfa(edge[i].from);
		int tf = un.getfa(edge[i].to);
		if(ff != tf)
		{
			un.fa[ff] = tf;
			tmp++;
			if(tmp == S)
				return edge[i].dist;
		}
	}
	return -1;
}

int main()
{
	int nnn;
	scanf("%d", &nnn);
	while(nnn--)
		printf("%.2f\n", Kruskal());//直接求最小生成树即可
	return 0;
}