Splay&LCT

Splay && LCT

\(\text{Splay}\)

基本操作

1.\(Zig \& Zag\)

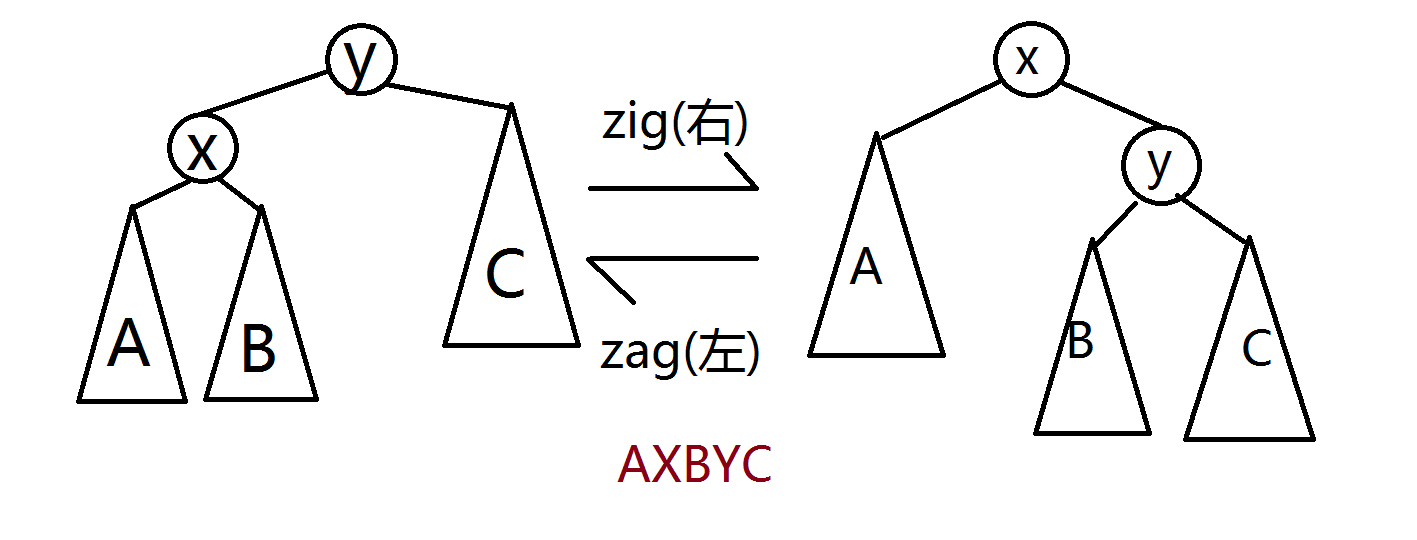
其思想是维护中序遍历不变

实现中我们不真的用\(Zig\)或\(Zag\)

而是注意到他们调用的左右永远是反的

一个函数就可以实现，一定每次看图

inline void rotate(re int x){
	re int y=fa[x],z=fa[y],l=*son[x]^x,r=l^1;
	if(fa[y])*son[z]==y?*son[z]=x:son[z][1]=x;fa[x]=z;
	son[y][l]=son[x][r];fa[son[y][l]]=y;
	son[x][r]=y;fa[y]=x;
	pushup(x);pushup(y);
}

\(2.Splay\)

有三种情况\(Zig/Zag\)和\(Zig+Zig/Zag+Zag\)和\(Zig+Zag/Zag+Zig\)(永远从下往上)

记住一句话:

后面两个操作只有\(x\)与它父亲不共线就转它两次，否则转它一次

inline void Splay(re int x){
	pushdown(x);
	while(fa[x]){
		if(fa[fa[x]])pushdown(fa[fa[x]]);pushdown(fa[x]);pushdown(x);
		if(fa[fa[x]])((*son[fa[fa[x]]]==fa[x])^(*son[fa[x]]==x))?rotate(x):rotate(fa[x]);
		rotate(x);
	}

\(\text{LCT}\)

\(\text{Blog}\)

定义：

一种用来解决动态树上问题的数据结构

\(1.\)虚实链

每一个\(Splay\)维护的是一条从上到下按在原树中深度严格递增的路径，且中序遍历Splay得到的每个点的深度序列严格递增。

在辅助树上,每个点与自己儿子的链为实链

辅助树的根与其\(LCT\)的父亲的链为虚链

基本操作

\(0.isroot\)查询一个点是否为\(Splay\)的根

inline char isroot(re int x){return *son[fa[x]]^x&&son[fa[x]][1]^x;}

\(1.Access\)

表示把\(x\)与其实儿子边变虚，把到辅助树根链上边变实

inline void Access(re int x){re int y=0;while(x){Splay(x);son[x][1]=y;pushup(x);y=x;x=fa[x];}}

\(2.Evert\)

表示把\(x\)变为原树的根

注意光是变为辅助树的根是不够的还要把深度互换

inline void Reverse(re int x){rev[x]^=1;swap(*son[x],son[x][1]);}
inline void Evert(re int x){Access(x);Splay(x);Reverse(x);}

\(3.Link\)

inline void Link(re int x,re int y){Evert(x);fa[x]=y;}

\(4.Cut\)

inline void Cut(re int x,re int y){Evert(x);Access(y);Splay(y);fa[x]=*son[y]=0;pushup(y);}

\(5.Query\):查询\(x\)到\(y\)一些信息

inline int Query(re int x,re int y){Evert(x);Access(y);Splay(y);return **;}