Sigmoid函数与Softmax函数的理解

1. Sigmod 函数

1.1 函数性质以及优点

其实logistic函数也就是经常说的sigmoid函数，它的几何形状也就是一条sigmoid曲线（S型曲线）。

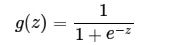
其中z是一个线性组合，比如z可以等于：b + w1*x1 + w2*x2。通过代入很大的正数或很小的负数到g(z)函数中可知，其结果趋近于0或1

A logistic function or logistic curve is a common “S” shape (sigmoid curve).

也就是说，sigmoid函数的功能是相当于把一个实数压缩至0到1之间。当z是非常大的正数时，g(z)会趋近于1，而z是非常小的负数时，则g(z)会趋近于0

压缩至0到1有何用处呢？用处是这样便可以把激活函数看作一种“分类的概率”，比如激活函数的输出为0.9的话便可以解释为90%的概率为正样本。

优点：

1、Sigmoid函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。

2、连续函数，便于求导。

1.2 函数缺点

sigmoid也具有自身的缺陷。

第一点，最明显的就是饱和性，从上图也不难看出其两侧导数逐渐趋近于0，即 $\lim_{x \rightarrow \infty}{f'(x)} = 0$ 。具体来说，在反向传播的过程中，sigmoid的梯度会包含了一个 $f'(x)$ 因子（sigmoid关于输入的导数），因此一旦输入落入两端的饱和区， $f'(x)$ 就会变得接近于0，导致反向传播的梯度也变得非常小，此时网络参数可能甚至得不到更新，难以有效训练，这种现象称为梯度消失。一般来说，sigmoid网络在5层之内就会产生梯度消失现象。

第二点，激活函数的偏移现象。sigmoid函数的输出值均大于0，使得输出不是0的均值，这会导致后一层的神经元将得到上一层非0均值的信号作为输入，这会对梯度产生影响。。

第三点，计算复杂度高，因为sigmoid函数是指数形式。

1.3 Sigmod函数求导

sigmod 求导过程很简单，可以手动推导。

2. Softmax 函数

2.1 Softmax函数表达式与性质

softmax函数，又称归一化指数函数。它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。下图展示了softmax的计算方法：

下面这张图便于理解：

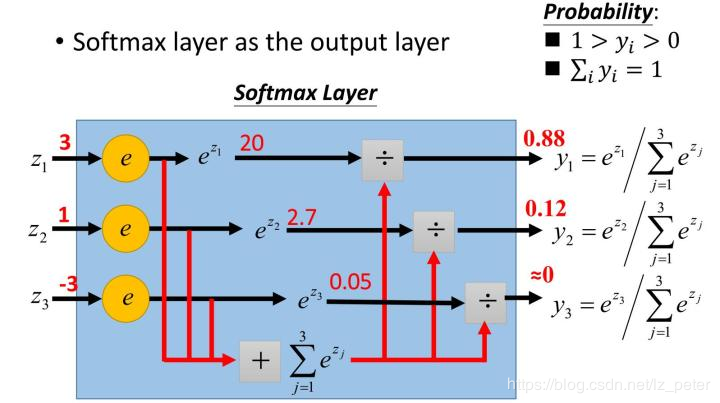
softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

由于Softmax函数先拉大了输入向量元素之间的差异（通过指数函数），然后才归一化为一个概率分布，在应用到分类问题时，它使得各个类别的概率差异比较显著，最大值产生的概率更接近1，这样输出分布的形式更接近真实分布。

2.2Softmax函数的解释

Softmax可以由三个不同的角度来解释。从不同角度来看softmax函数，可以对其应用场景有更深刻的理解。

2.2.1 是arg max的一种平滑近似

softmax可以当作arg max的一种平滑近似，与arg max操作中暴力地选出一个最大值（产生一个one-hot向量）不同，softmax将这种输出作了一定的平滑，即将one-hot输出中最大值对应的1按输入元素值的大小分配给其他位置。

2.2.2 归一化产生一个概率分布

Softmax函数的输出符合指数分布族的基本形式

$P(\mathbf{y};\theta)=h(\mathbf{y})\exp(\theta^\top T(\mathbf{y})-A(\theta))\tag{6}$

其中 $\theta\equiv\mathbf{1},\ h(\mathbf{y})=1/Z,\ T(\mathbf{y})=\mathbf{y},\ A(\theta)=0$ 。

不难理解，softmax将输入向量归一化映射到一个类别概率分布，即 $n$ 个类别上的概率分布（前文也有提到）。这也是为什么在深度学习中常常将softmax作为MLP的最后一层，并配合以交叉熵损失函数（对分布间差异的一种度量）。

2.2.3 产生概率无向图的联合概率

从概率图模型的角度来看，softmax的这种形式可以理解为一个概率无向图上的联合概率。因此你会发现，条件最大熵模型与softmax回归模型实际上是一致的，诸如这样的例子还有很多。由于概率图模型很大程度上借用了一些热力学系统的理论，因此也可以从物理系统的角度赋予softmax一定的内涵。

3. 总结

• 如果模型输出为非互斥类别，且可以同时选择多个类别，则采用Sigmoid函数计算该网络的原始输出值。

• 如果模型输出为互斥类别，且只能选择一个类别，则采用Softmax函数计算该网络的原始输出值。

参考链接：

https://zhuanlan.zhihu.com/p/69771964 （有许多sigmod 和 softmax函数理解的例子）

https://zhuanlan.zhihu.com/p/79585726 （对softmax函数与交叉熵函数的理解）