深度学习面试题05：激活函数sigmod、tanh、ReLU、LeakyRelu、Relu6

目录

　　为什么要用激活函数

　　sigmod

　　tanh

　　ReLU

　　LeakyReLU

　　ReLU6

　　参考资料

---

为什么要用激活函数

在神经网络中，如果不对上一层结点的输出做非线性转换的话，再深的网络也是线性模型，只能把输入线性组合再输出（如下图），不能学习到复杂的映射关系，因此需要使用激活函数这个非线性函数做转换。

返回目录

sigmod

Sigmod激活函数和导函数分别为

对应的图像分别为：

  

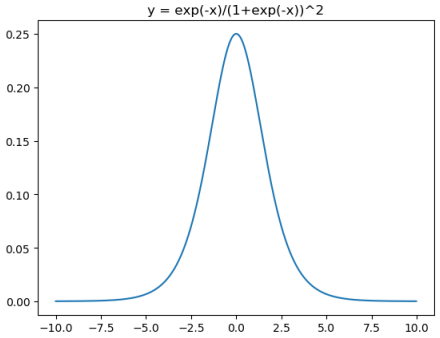
对应代码为：

Sigmod(x)的缺点：

①输出范围在0~1之间，均值为0.5，需要做数据偏移，不方便下一层的学习。

②当x很小或很大时，存在导数很小的情况。另外，神经网络主要的训练方法是BP算法，BP算法的基础是导数的链式法则，也就是多个导数的乘积。而sigmoid的导数最大为0.25，多个小于等于0.25的数值相乘，其运算结果很小。随着神经网络层数的加深，梯度后向传播到浅层网络时，基本无法引起参数的扰动，也就是没有将loss的信息传递到浅层网络，这样网络就无法训练学习了。这就是所谓的梯度消失。

返回目录

tanh

tanh是双曲函数中的一个，tanh()为双曲正切。在数学中，双曲正切“tanh”是由双曲正弦和双曲余弦这两种基本双曲函数推导而来。

tanh激活函数和导函数分别为

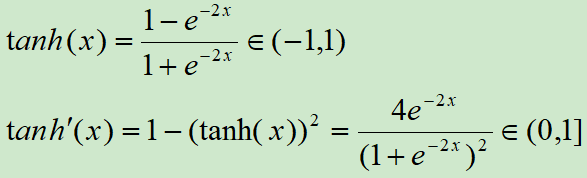
对应的图像分别为：

    

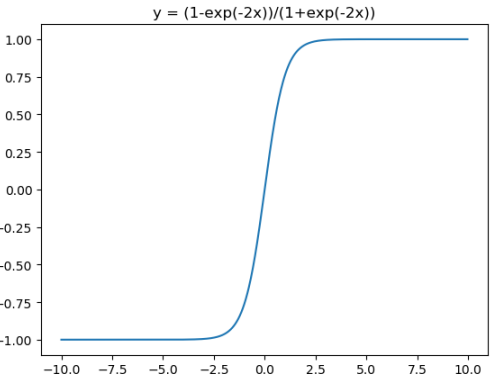
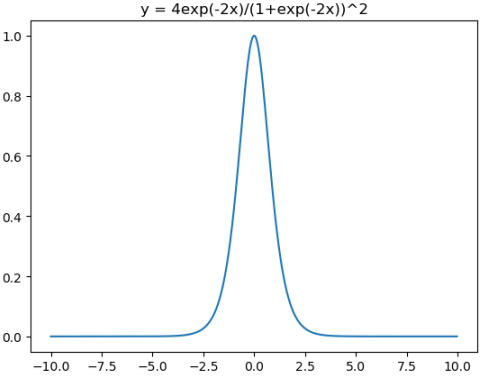
对应代码为：

在神经网络的应用中，tanh通常要优于sigmod的，因为tanh的输出在-1~1之间，均值为0，更方便下一层网络的学习。但有一个例外，如果做二分类，输出层可以使用sigmod，因为他可以算出属于某一类的概率

Sigmod(x)和tanh(x)都有一个缺点：在深层网络的学习中容易出现梯度消失，造成学习无法进行。

返回目录

ReLU

针对sigmod和tanh的缺点，提出了ReLU函数

线性整流函数（Rectified Linear Unit, ReLU），又称修正线性单元，是一种人工神经网络中常用的激活函数（activation function），通常指代以斜坡函数及其变种为代表的非线性函数。

ReLU激活函数和导函数分别为

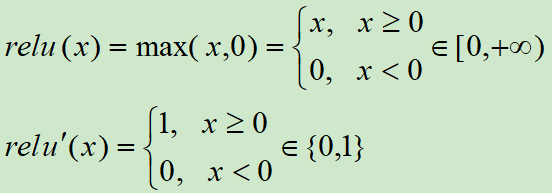
对应的图像分别为：

   

对应代码为：

Relu的一个缺点是当x为负时导数等于零，但是在实践中没有问题，也可以使用leaky Relu。

总的来说Relu是神经网络中非常常用的激活函数。

返回目录

LeakyReLU

Leaky ReLU激活函数和导函数分别为

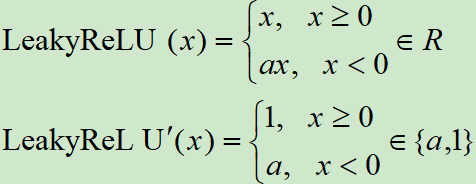
对应的图像分别为：

  

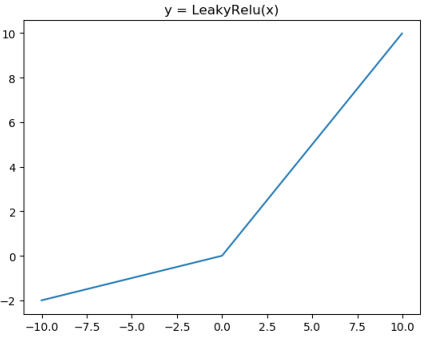
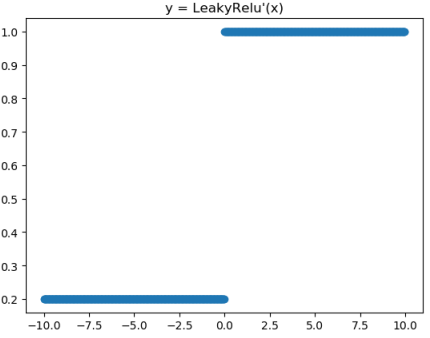
对应代码为：

返回目录

ReLU6

Relu在x>0的区域使用x进行线性激活，有可能造成激活后的值太大，影响模型的稳定性，为抵消ReLU激励函数的线性增长部分，可以使用Relu6函数

ReLU激活函数和导函数分别为

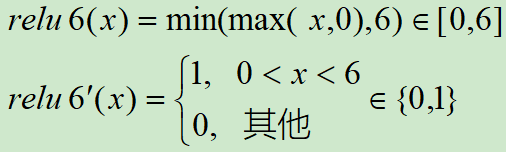
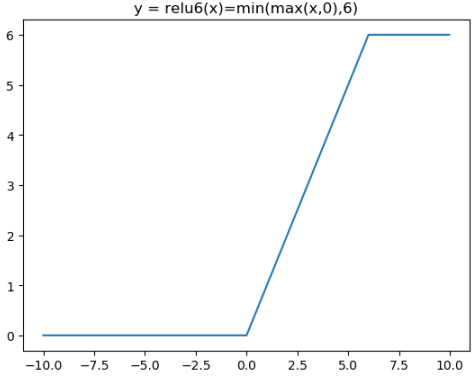
对应的图像分别为：

    

对应代码为：

返回目录

参考资料

吴恩达深度学习

神经网络中的梯度消失

https://www.cnblogs.com/mengnan/p/9480804.html

《图解深度学习与神经网络：从张量到TensorFlow实现》_张平