2019.11.11 模拟赛 T2 乘积求和

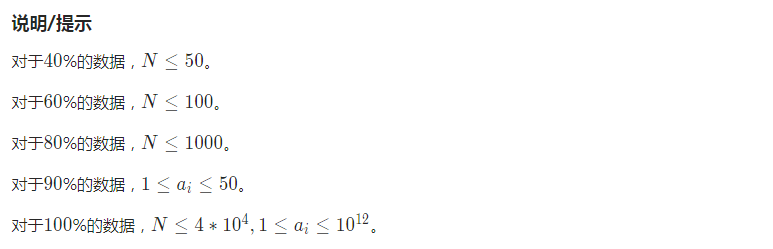
昨天 ych 的膜你赛，这道题我 O ( n⁴ ) 暴力拿了 60 pts。

这道题的做法还挺妙的，我搞了将近一天呢qwq

题解

60 pts

根据题目给出的式子，四层 for 循环暴力枚举统计答案即可；

#include<iostream>
#include<cstdio>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
const long long mod=1e12+;
int n;
long long ans,a[];
int main()
{
    freopen("multiplication.in","r",stdin);
    freopen("multiplication.out","w",stdout);
    n=read();
    for(int i=;i<=n;i++) a[i]=read();
    for(int l=;l<=n;l++)
        for(int r=l;r<=n;r++)
            for(int i=l;i<=r;i++)
                for(int j=i+;j<=r;j++)
                    if(a[i]>a[j])
                        ans=(ans+a[i]*a[j]%mod)%mod;
    printf("%lld\n",ans);
    return ;
}

80 pts

方法一：预处理 + O ( n² )

我们可以翻译一下题目中给出的式子：

就是求所有区间中每个区间的逆序对乘积；

那么我们可以提前预处理出每个区间的答案，再统计答案；

时间复杂的 O ( n² )，期望得分 80 pts；

for(int i=;i<=n;i++)
    {
        for(int j=i;j<=n;j++)
        {
            f[i][j]=f[i][j-];
            if(a[j]<a[i]) f[i][j]=(f[i][j]+a[i]*a[j]%mod)%mod;
        }
    }
    for(int i=;i<=n;i++)
    {
        for(int j=i+;j<=n;j++)
        {
            ans=(ans+i*f[i][j])%mod;
        }
    }

方法二：归并排序

考虑一对逆序对 ( a_i , a_j ) 会在所有的区间内出现几次 。

因为同时包含 a_i 和 a_j 的最小区间是 [ i , j ]，所以左端点小于等于 i，右端点大于等于 j 的所有区间也包含，所有共有 i * ( n - j + 1 )；

所以我们可以去找出所有的逆序对，然后去计算他们对答案的贡献；

求逆序对，我们可以用归并排序；

具体思路就是在两部分合并的过程中，如果左半部分的某个数 a_i 大于右半部分某个数 a_j ，这时候从 a_i ~ a_mid 都会与 a_j 产生一组逆序对，我们统计答案就好了；

#include<iostream>
#include<cstdio>
using namespace std;
long long read()
{
    char ch=getchar();
    long long a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
const long long mod=1e12+;
const int N=5e4;
long long n,ans;
struct node
{
    long long val,id;
}a[N],c[N];
void gb_sort(int l,int r)
{
    if(l==r) return ;
    int mid=(l+r)>>;
    gb_sort(l,mid);
    gb_sort(mid+,r);
    int i=l,j=mid+;
    int k=l-;
    while(i<=mid&&j<=r)
    {
        if(a[i].val>a[j].val)
        {
            for(int l=i;l<=mid;l++)
                ans=(ans+a[l].val*a[j].val%mod*a[l].id*(n-a[j].id+)%mod)%mod;
            //printf("%lld\n",ans);
            c[++k].val=a[j].val;c[k].id=a[j].id;
            j++;
        }
        else
        {
            c[++k].val=a[i].val;c[k].id=a[i].id;
            i++;
        }
    }
    while(i<=mid)
    {
        c[++k].val=a[i].val;c[k].id=a[i].id;
        i++;
    }
    while(j<=r)
    {
        c[++k].val=a[j].val;c[k].id=a[j].id;
        j++;
    }
    for(int i=l;i<=r;i++)
    {
        a[i].id=c[i].id;
        a[i].val=c[i].val;
    }
}
int main()
{
    freopen("multiplication.in","r",stdin);
    freopen("multiplication.out","w",stdout);
    n=read();
    for(int i=;i<=n;i++)
    {
        a[i].val=read();
        a[i].id=i;
    }
    gb_sort(,n);
    printf("%lld\n",ans);
    return ;
}

90 pts

发现正是归并排序统计答案的时候是 O ( n ) 的，使得复杂度升高了；

我们想能不能优化下：

还是按照上面的思路，如果在合并的时候有 a_i > a_j ，则 a_i ~ a_mid 都会与 a_j 产生逆序对，那么 a_j 产生的贡献之和就是：

a_i * a_j * i * ( n - j + 1 ) + a_i+1 * a_j * ( i+1 )  * ( n - j + 1 ) + …… + a_mid * a_j * mid * ( n - j + 1 )

我们将 a_j * ( n - j + 1 ) 提出来就是：

a_j * ( n - j + 1 ) * [ a_i * i + a_i+1 * ( i+1 ) + a_i+2 * ( i+2 ) + a_mid * mid ]

也就是说，我们可以统计在 a_j 之前的所有数中，每个比 a_j 大的数 a_i 再乘上 a_i 的下标 i 的和是多少，记为 sum；

则 sum = a_i * i + a_i+1 * ( i+1 ) + a_i+2 * ( i+2 ) + a_mid * mid，那么 a_j 对答案的贡献就是：sum * a_j * ( n - j + 1 )

然后我们发现这东西可以用权值树状数组来维护：

每个下标为 i 的数组维护 a_i * i 的值是多少，当我们对原数列的数依次放到树状数组的时候，由于前面的数已经放进去了，我们可以去统计有所有比当前数大的数（可以与当前数构成逆序对的数）它们的 a_i * i 的值的和是多少；由于是权值树状数组，所以比当前数要大的数在树状数组里的编号是比当前数的编号大的，所以我们可以求后缀和；但是由于我们不会求后缀和，所以我们可以把权值树状数组的编号反过来存，大的在前面，小的在后面，这样就转化成了我们熟悉的前缀和啦；

但是由于每个元素的权值范围较大，且逆序对的产生只与两个数的大小关系有关，与两个数具体是多少无关，所以我们可以先离散化；

时间复杂度 O ( nlog n )，期望得分 90 pts；

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
long long read()
{
    char ch=getchar();
    long long a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
const long long mod=1e12+;
const long long N=1e5;
long long n;
long long ans,c[N];
struct node
{
    long long id,val,rank;
}a[N];
bool cmp1(node x,node y)
{
    if(x.val!=y.val)
     return x.val<y.val;
    return x.id<y.id;
}
bool cmp2(node x,node y)
{
    return x.id<y.id;
}
void lsh()                                //离散化
{
    sort(a+,a++n,cmp1);                 //先按照大小排序
    for(long long i=;i<=n;i++) a[i].rank=i; //按大小关系给每个元素分个排名,就是离散化之后的大小
    sort(a+,a++n,cmp2);                 //再按照在原序列里的编号排回去
}
long long lowbit(long long x)
{
    return x&(-x);
}
long long ask(long long x)                //树状数组求[1,x]的和
{
    long long y=;
    for(long long i=x;i;i-=lowbit(i)) y=(y+c[i]+mod)%mod;
    return y;
}
void add(long long x,long long y)         //将第x个数加y
{
    for(long long i=x;i<=n;i+=lowbit(i)) c[i]=(c[i]+y+mod)%mod;
}
int main()
{
    freopen("multiplication.in","r",stdin);
    freopen("multiplication.out","w",stdout);
    n=read();
    for(long long i=;i<=n;i++)
    {
        a[i].val=read();                  //每个元素的大小
        a[i].id=i;                        //每个元素在原序列里的编号(是第几个)
    }
    lsh();                                //离散化
    for(long long i=;i<=n;i++)           //依次将每个数丢进树状数组
    {
        long long sum=ask(n-a[i].rank+); //求一次前缀和,注意这里大小编号是反着的
        ans=(ans+sum*a[i].val%mod*(n-a[i].id+)%mod)%mod;   //算当前元素对答案的贡献
        add(n-a[i].rank+,a[i].id*a[i].val%mod);  //将当前元素丢进树状数组里,维护的是这个数的下标*权值
    }
    printf("%lld\n",ans%mod);
    return ;
}

100 pts

不是，我时间复杂度 O ( nlog n ) 跑的飞快啊，怎么还没满分？

有一个小细节需要注意：

我们的模数是 10¹² +7，两个数相乘很可能爆 long long 的。

这时候我们就要用到龟速乘了qwq：

龟速乘

龟速乘好像就是来弥补快速幂的 bug 的，虽然计算速度真的龟速。。。

它的原理是这样的：

假如我们现在要计算一个简单的式子：3 * 23

然后我们将 23 用二进制表示一下子：( 23 )₁₀ = ( 10111 )₂

那么我们可以将 23 写成这个形式：23 = 2⁰ + 2¹ + 2² + 2⁴

然后我们再将其代回原式：3 * 23 = 3 * ( 2⁰ + 2¹ + 2² + 2⁴ ) = 3 * 2⁰ + 3 * 2¹ + 3 * 2² + 3 * 2⁴

然后我们发现每次加的 3 的系数都是原来的两倍，这一点与快速幂类似；

代码实现：

long long slow_pow(long long a,long long b)   //龟速乘计算a*b
{
    long long tot=;
    while(b)
    {
        if(b&) tot=(tot+a+mod)%mod;
        a=(a+a+mod)%mod;                      //每次变为原来的2倍
        b>>=;
    }
    return tot;
}

然后套上龟速乘，这个题最后的坑就被我们填完了，完整AC代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
long long read()
{
    char ch=getchar();
    long long a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
const long long mod=1e12+;
const long long N=1e5;
long long n;
long long ans,c[N];
struct node
{
    long long id,val,rank;
}a[N];
long long slow_pow(long long a,long long b)   //龟速乘计算a*b
{
    long long tot=;
    while(b)
    {
        if(b&) tot=(tot+a+mod)%mod;
        a=(a+a+mod)%mod;                      //每次变为原来的2倍
        b>>=;
    }
    return tot;
}
bool cmp1(node x,node y)
{
    if(x.val!=y.val)
     return x.val<y.val;
    return x.id<y.id;
}
bool cmp2(node x,node y)
{
    return x.id<y.id;
}
void lsh()                                //离散化
{
    sort(a+,a++n,cmp1);                 //先按照大小排序
    for(long long i=;i<=n;i++) a[i].rank=i; //按大小关系给每个元素分个排名,就是离散化之后的大小
    sort(a+,a++n,cmp2);                 //再按照在原序列里的编号排回去
}
long long lowbit(long long x)
{
    return x&(-x);
}
long long ask(long long x)                //树状数组求[1,x]的和
{
    long long y=;
    for(long long i=x;i;i-=lowbit(i)) y=(y+c[i]+mod)%mod;
    return y;
}
void add(long long x,long long y)         //将第x个数加y
{
    for(long long i=x;i<=n;i+=lowbit(i)) c[i]=(c[i]+y+mod)%mod;
}
int main()
{
    freopen("multiplication.in","r",stdin);
    freopen("multiplication.out","w",stdout);
    n=read();
    for(long long i=;i<=n;i++)
    {
        a[i].val=read();                  //每个元素的大小
        a[i].id=i;                        //每个元素在原序列里的编号(是第几个)
    }
    lsh();                                //离散化
    for(long long i=;i<=n;i++)           //依次将每个数丢进树状数组
    {
        long long sum=ask(n-a[i].rank+); //求一次前缀和,注意这里大小编号是反着的
        ans=(ans+slow_pow(slow_pow(sum,a[i].val)%mod,(n-a[i].id+))%mod)%mod;   //算当前元素对答案的贡献
        add(n-a[i].rank+,slow_pow(a[i].id,a[i].val)%mod);  //将当前元素丢进树状数组里,维护的是这个数的下标*权值
    }
    printf("%lld\n",ans%mod);
    return ;
}

这道题让我重新温习了我不熟悉的数据结构，让我距目标更近了一步呢，最后，CSP 加油！