Comet OJ Contest #13 简要题解

C2

首先用并查集维护\(1\)的连通块，然后用另外一个并查集维护第\(i\)行中，第\(j\)列之后的第一个\(0\)的位置，就是如果当前位置是\(1\)那么它的父亲是它右边的格子，否则是它自己。

时间复杂度\(O(nm\log m+nq)\)。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
const int N = 1003, d[2][4] = {{0, 1, 0, -1}, {1, 0, -1, 0}};
int n, m, q, fa[N][N], cnt, Fa[N * N], Siz[N * N];
char str[N];
bool a[N][N];
inline int getfa(int x, int y){
	return (fa[x][y] == y) ? y : (fa[x][y] = getfa(x, fa[x][y]));
}
inline int Getfa(int x){
	return (Fa[x] == x) ? x : (Fa[x] = Getfa(Fa[x]));
}
inline int id(int x, int y){return (x - 1) * m + y;}
inline void work(int x, int y){
	for(Rint i = 0;i < 4;i ++){
		int nx = x + d[0][i], ny = y + d[1][i];
		if(nx >= 1 && nx <= n && ny >= 1 && ny <= m && a[nx][ny]){
			int fa1 = Getfa(id(x, y)), fa2 = Getfa(id(nx, ny));
			if(fa1 != fa2){
				if(Siz[fa1] > Siz[fa2]) swap(fa1, fa2);
				Fa[fa1] = fa2; Siz[fa2] += Siz[fa1]; -- cnt;
			}
		}
	}
}
int main(){
	scanf("%d%d", &n, &m);
	for(Rint i = 1;i <= n * m;i ++) Fa[i] = i, Siz[i] = 1;
	for(Rint i = 1;i <= n;i ++){
		scanf("%s", str + 1);
		for(Rint j = 1;j <= m;j ++){
			a[i][j] = (str[j] == '1'); fa[i][j] = j + a[i][j]; cnt += a[i][j];
		}
		fa[i][m + 1] = m + 1;
	}
	for(Rint i = 1;i <= n;i ++)
		for(Rint j = 1;j <= m;j ++)
			if(a[i][j]) work(i, j);
	scanf("%d", &q);
	while(q --){
		int x1, y1, x2, y2;
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		for(Rint i = x1;i <= x2;i ++){
			int j = y1;
			while((j = getfa(i, j)) <= y2){
				++ cnt; a[i][j] = 1; fa[i][j] = j + 1;
				work(i, j);
			}
		}
		printf("%d\n", cnt);
	}
}

D

首先甩上来一个单位根反演。

\[F_n=\frac{1}{2}((b+\sqrt a)^n+(b-\sqrt a)^n)
\]

于是你发现\(p\)不是质数，于是就自闭了。

然后你想起了BJ人民的扩域做法，就是搞一个域\(Z[\sqrt a]=\{x+y\sqrt a|x,y\in Z\}\)，然后直接计算快速幂。但是你绝望地发现，最后有一个\(\frac{1}{2}\)，于是你又废了。

然后你去看题解，发现逆向思维是非常重要的。平常大家都是递推公式\(\rightarrow\)通项公式，但是你有想到通项公式\(\rightarrow\)递推公式吗？

根据特征方程的理论，设\(F_n=AF_{n-1}+BF_{n-2}\)，那么\(x^2-Ax-B=0\)的两根为\(b\pm \sqrt a\)，所以\(A=b+\sqrt a+b-\sqrt a=2b\)，\(B=-(b+\sqrt a)(b-\sqrt a)=a-b^2\)。然后用矩阵快速幂求出\(F_n\)就可以了。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
int T;
LL a, b, p, n;
inline void upd(LL &a, LL b){a += b; if(a >= p) a -= p;}
struct Matrix {
	LL x[2][2];
	inline Matrix(){memset(x, 0, sizeof x);}
	inline Matrix operator = (const Matrix &o){
		memcpy(x, o.x, sizeof x);
		return *this;
	}
	inline Matrix operator * (const Matrix &o) const {
		Matrix res;
		for(Rint i = 0;i < 2;i ++)
			for(Rint k = 0;k < 2;k ++)
				for(Rint j = 0;j < 2;j ++)
					upd(res.x[i][j], (__int128) x[i][k] * o.x[k][j] % p);
		return res;
	}
} A, B;
inline Matrix kasumi(Matrix A, LL b){
	Matrix res; res.x[0][0] = res.x[1][1] = 1;
	while(b){
		if(b & 1) res = res * A;
		A = A * A; b >>= 1;
	}
	return res;
}
int main(){
	scanf("%d", &T);
	while(T --){
		scanf("%lld%lld%lld%lld", &n, &a, &b, &p); a %= p; b %= p;
		if(n == 0){puts("1"); continue;}
		if(n == 1){printf("%lld\n", b); continue;}
		A.x[0][0] = 2 * b % p; A.x[0][1] = (a + p - (__int128) b * b % p) % p;
		A.x[1][0] = 1; B.x[0][0] = b; B.x[1][0] = 1;
		B = kasumi(A, n - 1) * B;
		printf("%lld\n", B.x[0][0]);
	}
}

E

这是一个看上去很吓人的计算几何。

首先我们发现，这个范围实际上就是两个相距\(2d\)的平行线之间的部分，于是我们枚举其中一个平行线，发现它总能经过一个点，我们枚举这个点\(A\)，看它在哪些时候可以覆盖另外一个点\(B\)。

分类讨论。

1. \(dis(A,B)\le 2d\)，设\(\alpha=\arctan\frac{y_B-y_A}{x_B-x_A}\)，则直线倾角的范围是\([\alpha,\alpha+\pi]\)

2. \(dis(A,B)>2d\)，设\(\beta=\arcsin\frac{2d}{dis(A,B)}\)，则直线倾角的范围是\([\alpha,\alpha+\beta]\cup[\alpha+\pi-\beta,\alpha+\pi]\)

如果看不懂的话，就来看个图。

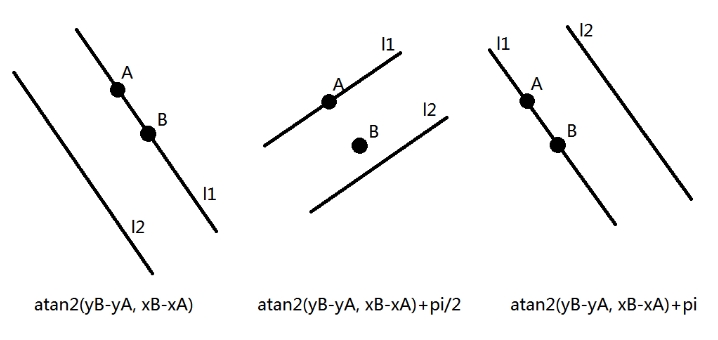
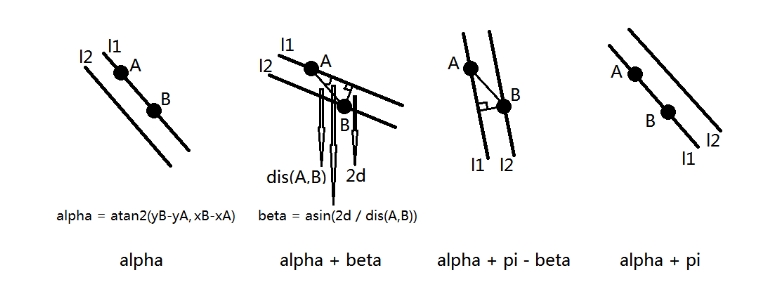
于是问题就转化成了给出一堆区间，求一个点至多被覆盖多少次。这是一个经典题

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
const int N = 16003;
const double PI = acos(-1);
int n, d, x[N], y[N], ans, tag[N], len, tot;
double l[N], r[N], val[N];
inline void add(double x, double y){
	if(x < 0 && y < 0) x += PI * 2, y += PI * 2;
	if(x < 0){
		l[++ tot] = x + 2 * PI; r[tot] = 2 * PI; val[++ len] = x + 2 * PI; val[++ len] = 2 * PI;
		l[++ tot] = 0; r[tot] = y; val[++ len] = 0; val[++ len] = y;
	} else {
		l[++ tot] = x; r[tot] = y; val[++ len] = x; val[++ len] = y;
	}
}
inline void work(int p){
	len = tot = 0;
	for(Rint i = 1;i <= n;i ++) if(i != p){
		double alpha = atan2(y[i] - y[p], x[i] - x[p]), dis = (x[i] - x[p]) * (x[i] - x[p]) + (y[i] - y[p]) * (y[i] - y[p]);
		if(dis <= d * d){
			add(alpha, alpha + PI);
		} else {
			double beta = asin(1.0 * d / sqrt(dis));
			add(alpha, alpha + beta); add(alpha + PI - beta, alpha + PI);
		}
	}
	sort(val + 1, val + len + 1);
	len = unique(val + 1, val + len + 1) - val - 1;
	for(Rint i = 1;i <= tot;i ++){
		int a = lower_bound(val + 1, val + len + 1, l[i]) - val, b = lower_bound(val + 1, val + len + 1, r[i]) - val + 1;
		++ tag[a]; -- tag[b];
	}
	for(Rint i = 1;i <= len;i ++){
		ans = max(ans, tag[i] += tag[i - 1]); tag[i - 1] = 0;
	} tag[len] = 0;
}
int main(){
	scanf("%d%d", &n, &d); d <<= 1;
	for(Rint i = 1;i <= n;i ++) scanf("%d%d", x + i, y + i);
	for(Rint i = 1;i <= n;i ++) work(i);
	printf("%d", ans + 1);
}