ural1519插头DP

1519. Formula 1

Time limit: 1.0 second

Memory limit: 64 MB

Background

Regardless of the fact, that Vologda could not get rights to hold the Winter Olympic games of 20**, it is well-known, that the city will conduct one of the Formula 1 events. Surely, for such an important
thing a new race circuit should be built as well as hotels, restaurants, international airport - everything for Formula 1 fans, who will flood the city soon. But when all the hotels and a half of the restaurants were built, it appeared, that at the site for
the future circuit a lot of gophers lived in their holes. Since we like animals very much, ecologists will never allow to build the race circuit over the holes. So now the mayor is sitting sadly in his office and looking at the map of the circuit with all
the holes plotted on it.

Problem

Who will be smart enough to draw a plan of the circuit and keep the city from inevitable disgrace?

Of course, only true professionals - battle-hardened programmers from the first team of local technical
university!.. But our heroes were not looking for easy life and set much more difficult problem: "Certainly, our mayor will be glad, if we find how many ways of building the circuit are there!" - they said.

It should be said, that the circuit in Vologda is going to be rather simple. It will be a rectangleN*M cells in size with a single circuit segment built through each
cell. Each segment should be parallel to one of rectangle's sides, so only right-angled bends may be on the circuit. At the picture below two samples are given for N = M = 4 (gray squares mean gopher holes, and the bold black
line means the race circuit). There are no other ways to build the circuit here.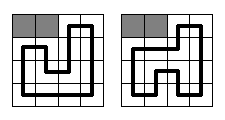

Input

The first line contains the integer numbers N and M (2 ≤ N, M ≤ 12). Each of the next N lines contains M characters,
which are the corresponding cells of the rectangle. Character "." (full stop) means a cell, where a segment of the race circuit should be built, and character "*" (asterisk) - a cell, where a gopher hole is located.

Output

You should output the desired number of ways. It is guaranteed, that it does not exceed 263-1.

Samples

input	output
4 4 **.. .... .... ....	2
4 4 .... .... .... ....	6

分析看这(转):http://blog.sina.com.cn/s/blog_51cea4040100gmky.html

依照上面链接分析就非常明白了，情况分清楚了就好写了

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <algorithm>
#include <map>
#include <cmath>
#include <iomanip>
#define INF 99999999
typedef long long LL;
using namespace std;

const int MAX=300000+10;//最多的有效状态
const int N=10+10;
int n,m,size,index;
int mp[N][N],total[2],bit[N],ex,ey;//ex,ey记录最后一个非限制点,total记录有多少状态
int head[MAX],Next[MAX],Hash[MAX];//Hash用哈希查询状态,才用邻接表查询
//对于第i,j格仅仅须要用到第i,j-1格到达,所以才用滚动数组节省内存
LL dp[2][MAX],state[2][MAX],sum;//state记录对应状态,dp记录对应状态可到达的数量

void Init(){
	memset(mp,0,sizeof mp);
	sum=size=index=0;
	total[index]=1;
	state[index][1]=0;//初始化仅仅有一种可到达状态:没有不论什么插头
	dp[index][1]=1;
}

void HashCalState(LL s,LL num){
	int pos=s%MAX;
	for(int i=head[pos];i != -1;i=Next[i]){
		if(state[index][Hash[i]] == s){
			dp[index][Hash[i]]+=num;
			return;
		}
	}
	++total[index];
	state[index][total[index]]=s;
	dp[index][total[index]]=num;
	//头插法
	Hash[size]=total[index];
	Next[size]=head[pos];
	head[pos]=size++;
}

void DP(){//才用4进制进行DP,x*4^y=x*2^(2*y)
	for(int i=1;i<=n;++i){
		for(int k=1;k<=total[index];++k)state[index][k]<<=2;//由上移一行到达这一行(i,0格)在上一行的0号插头前面再加一个插头,去掉最后一个插头(最后一个插头肯定为0)
		for(int j=1;j<=m;++j){//求由i,j-1到达i,j的状态以及状态数
			memset(head,-1,sizeof head);
			size=0;
			index=index^1;
			total[index]=0;
			for(int k=1;k<=total[index^1];++k){//枚举上一格的状态,用来到达i,j某个状态
				LL s=state[index^1][k];//取状态
				LL num=dp[index^1][k];//取到达对应状态个数
			 	int p=(s>>bit[j-1])%4;//取第j位
				int q=(s>>bit[j])%4;//取第j+1位
				if(!mp[i][j]){//i,j有限制不能通过,必须绕过
					if(p+q == 0)HashCalState(s,num);//仅仅有p=q=0才干到达p'=q'=0的状态,才用哈希计算到达的状态以及个数
				}else if(p+q == 0){//i,j无限制则必须有两个插头通过(一进一出)
					if(!mp[i+1][j] || !mp[i][j+1])continue;
					s=s+(1<<bit[j-1])+2*(1<<bit[j]);//创建新的连通块(添加第j,j+1个插头)
					HashCalState(s,num);
				}else if(!p && q){//p无插头,q有插头,则新状态须要添加一个插头
					if(mp[i][j+1])HashCalState(s,num);//状态不变,连通块不变
					if(mp[i+1][j]){
						s=s+q*(1<<bit[j-1])-q*(1<<bit[j]);
						HashCalState(s,num);
					}
				}else if(p && !q){//同上
					if(mp[i+1][j])HashCalState(s,num);
					if(mp[i][j+1]){
						s=s-p*(1<<bit[j-1])+p*(1<<bit[j]);
						HashCalState(s,num);
					}
				}else if(p+q == 2){//p=q=1,合并连通块
					int b=1;
					for(int t=j+1;t<=m;++t){//寻找近期的匹配的括号
						int v=(s>>bit[t])%4;
						if(v == 1)++b;
						if(v == 2)--b;
						if(b == 0){
							s=s+(1<<bit[t])-2*(1<<bit[t]);//将右括号变为左括号
							break;
						}
					}
					s=s-(1<<bit[j-1])-(1<<bit[j]);
					HashCalState(s,num);
				}else if(p+q == 4){//p=q=2,同上
					int b=1;
					for(int t=j-2;t>=0;--t){//寻找近期的匹配括号
						int v=(s>>bit[t])%4;
						if(v == 2)++b;
						if(v == 1)--b;
						if(b == 0){
							s=s-(1<<bit[t])+2*(1<<bit[t]);//将左括号变为右括号
							break;
						}
					}
					s=s-2*(1<<bit[j-1])-2*(1<<bit[j]);
					HashCalState(s,num);
				}else if(p == 1 && q == 2){//合并连通块,仅仅有最后一格的时候才连成整个回路
					if(i == ex && j == ey)sum+=num;
				}else if(p == 2 && q == 1){
					s=s-2*(1<<bit[j-1])-(1<<bit[j]);
					HashCalState(s,num);
				}
			}
		}
	}
}

int main(){
	char ch;
	for(int i=0;i<N;++i)bit[i]=i<<1;//求4进制的某位用2进制求须要右移的位数*2
	while(~scanf("%d%d",&n,&m)){
		Init();
		for(int i=1;i<=n;++i){
			getchar();
			for(int j=1;j<=m;++j){
				scanf("%c",&ch);
				mp[i][j]=(ch == '.');
				if(ch == '.')ex=i,ey=j;
			}
		}
		DP();//插头DP
		printf("%lld\n",sum);
	}
	return 0;
}
/*
12 12
............
............
............
............
............
............
............
............
............
............
............
............
9 10
..........
..........
..........
..........
..........
..........
..........
..........
..........
*/

版权声明：本文博客原创文章，博客，未经同意，不得转载。