Codeforces Round #257 (Div. 1)A~C(DIV.2-C~E)题解
今天老师(orz sansirowaltz)让我们做了很久之前的一场Codeforces Round #257 (Div. 1),这里给出A~C的题解,对应DIV2的C~E。
1 second
256 megabytes
standard input
standard output
Jzzhu has a big rectangular chocolate bar that consists of n × m unit squares. He wants to cut this bar exactly k times. Each cut must meet the following requirements:
- each cut should be straight (horizontal or vertical);
- each cut should go along edges of unit squares (it is prohibited to divide any unit chocolate square with cut);
- each cut should go inside the whole chocolate bar, and all cuts must be distinct.
The picture below shows a possible way to cut a 5 × 6 chocolate for 5 times.
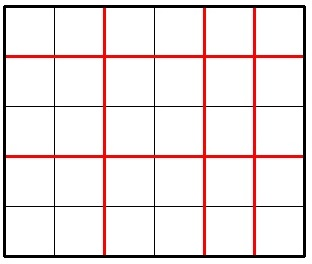
Imagine Jzzhu have made k cuts and the big chocolate is splitted into several pieces. Consider the smallest (by area) piece of the chocolate, Jzzhu wants this piece to be as large as possible. What is the maximum possible area of smallest piece he can get with exactly k cuts? The area of a chocolate piece is the number of unit squares in it.
A single line contains three integers n, m, k (1 ≤ n, m ≤ 109; 1 ≤ k ≤ 2·109).
Output a single integer representing the answer. If it is impossible to cut the big chocolate k times, print -1.
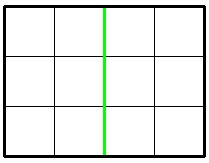
- 3 4 1
- 6
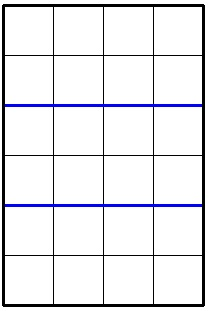
- 6 4 2
- 8
- 2 3 4
- -1
In the first sample, Jzzhu can cut the chocolate following the picture below:
In the second sample the optimal division looks like this:
In the third sample, it's impossible to cut a 2 × 3 chocolate 4 times.
这题是数学问题,感觉没什么好说的,就是注意long long和细节,很容易WA掉。
- #include<iostream>
- #include<cstdio>
- #include<algorithm>
- #include<cmath>
- using namespace std;
- int k;
- long long n,m;
- long long ans;
- int main()
- {
- scanf("%I64d%I64d%d",&n,&m,&k);
- if(n<k+1 && m<k+1)
- {
- if(n+m-2<k)
- {
- printf("%d\n",-1);
- return 0;
- }
- printf("%I64d\n",max((n/(k-m+2)),m/(k-n+2)));
- return 0;
- }
- if(n/(k+1)*m>m/(k+1)*n)
- printf("%I64d\n",n/(k+1)*m);
- else
- printf("%I64d\n",m/(k+1)*n);
- return 0;
- }
2 seconds
256 megabytes
standard input
standard output
Jzzhu is the president of country A. There are n cities numbered from 1 to n in his country. City 1 is the capital of A. Also there are mroads connecting the cities. One can go from city ui to vi (and vise versa) using the i-th road, the length of this road is xi. Finally, there are k train routes in the country. One can use the i-th train route to go from capital of the country to city si (and vise versa), the length of this route is yi.
Jzzhu doesn't want to waste the money of the country, so he is going to close some of the train routes. Please tell Jzzhu the maximum number of the train routes which can be closed under the following condition: the length of the shortest path from every city to the capital mustn't change.
The first line contains three integers n, m, k (2 ≤ n ≤ 105; 1 ≤ m ≤ 3·105; 1 ≤ k ≤ 105).
Each of the next m lines contains three integers ui, vi, xi (1 ≤ ui, vi ≤ n; ui ≠ vi; 1 ≤ xi ≤ 109).
Each of the next k lines contains two integers si and yi (2 ≤ si ≤ n; 1 ≤ yi ≤ 109).
It is guaranteed that there is at least one way from every city to the capital. Note, that there can be multiple roads between two cities. Also, there can be multiple routes going to the same city from the capital.
Output a single integer representing the maximum number of the train routes which can be closed.
- 5 5 3
1 2 1
2 3 2
1 3 3
3 4 4
1 5 5
3 5
4 5
5 5
- 2
- 2 2 3
1 2 2
2 1 3
2 1
2 2
2 3
- 2
思路:跑一遍最短路spfa,然后记录经过的边(如果普通边和铁路在某种情况下一样优则选择普通边),若其中有铁路就保留,反之不在最短路径中的铁路删除,cout删除的个数就OK了~
- #include<iostream>
- #include<cstdio>
- #include<algorithm>
- #include<cmath>
- #include<vector>
- #include<map>
- #include<queue>
- using namespace std;
- int n,m,k,x,y,z,cnt;
- struct sdt
- {
- int to,len;
- bool flag;
- };
- vector<sdt>v[100005];
- long long dis[100005];
- bool par[100005];
- void spfa()
- {
- priority_queue<pair<long long,int>,vector<pair<long long,int> >,greater<pair<long long,int> > >q;
- bool vis[100005]={0};
- q.push(make_pair(0,1));
- vis[1]=1;
- while(!q.empty())
- {
- int s=q.top().second;
- vis[s]=0;
- q.pop();
- for(int i=0;i<v[s].size();i++)
- {
- sdt p=v[s][i];
- if(dis[s]!=1e18 && dis[p.to]>dis[s]+p.len)
- {
- dis[p.to]=dis[s]+p.len;
- if(par[p.to]==1)
- {
- cnt--;
- par[p.to]=0;
- }
- if(p.flag==1)
- {
- ++cnt;
- par[p.to]=1;
- }
- if(!vis[p.to])
- {
- q.push(make_pair(dis[p.to],p.to));
- vis[p.to]=1;
- }
- }
- else if(dis[s]!=1e18 && dis[p.to]==dis[s]+p.len)
- {
- if(!par[p.to])continue;
- if(p.flag)continue;
- par[p.to]=0;
- cnt--;
- }
- }
- }
- }
- int main()
- {
- scanf("%d%d%d",&n,&m,&k);
- for(int i=1;i<=m;i++)
- {
- scanf("%d%d%d",&x,&y,&z);
- sdt p;
- p.to=y;
- p.len=z;
- p.flag=0;
- v[x].push_back(p);
- p.to=x;
- p.len=z;
- p.flag=0;
- v[y].push_back(p);
- }
- for(int i=1;i<=k;i++)
- {
- scanf("%d%d",&y,&z);
- sdt p;
- p.to=y;
- p.len=z;
- p.flag=1;
- v[1].push_back(p);
- p.to=1;
- p.len=z;
- p.flag=1;
- v[y].push_back(p);
- }
- for(int i=2;i<=n;i++)
- {
- dis[i]=1e18;
- }
- spfa();
- printf("%d\n",k-cnt);
- return 0;
- }
1 second
256 megabytes
standard input
standard output
Jzzhu has picked n apples from his big apple tree. All the apples are numbered from 1 to n. Now he wants to sell them to an apple store.
Jzzhu will pack his apples into groups and then sell them. Each group must contain two apples, and the greatest common divisor of numbers of the apples in each group must be greater than 1. Of course, each apple can be part of at most one group.
Jzzhu wonders how to get the maximum possible number of groups. Can you help him?
A single integer n (1 ≤ n ≤ 105), the number of the apples.
The first line must contain a single integer m, representing the maximum number of groups he can get. Each of the next m lines must contain two integers — the numbers of apples in the current group.
If there are several optimal answers you can print any of them.
- 6
- 2
6 3
2 4
- 9
- 3
9 3
2 4
6 8
- 2
- 0
思路:这是数论问题。显然若是偶数则随便组合,奇数的话,若是某质数的倍数随便组合(若在N以内此质数倍数个数为奇数,则2倍项留给偶数之后处理,否则立即匹配),当然要打标记是否用过。上述方式即可保证最优!易证。
- #include<iostream>
- #include<cstdio>
- #include<algorithm>
- #include<cmath>
- #include<vector>
- #include<map>
- #include<queue>
- #include<cstring>
- using namespace std;
- int n,cnt;
- bool vis[100005];
- vector<pair<int,int> >v;
- bool p[100005];
- void prime()
- {
- memset(p,1,sizeof(p));
- p[1]=0;
- for(int i=2;i<=n;i++)
- {
- if(p[i])
- {
- for(int j=i*2;j<=n;j+=i)
- {
- p[j]=0;
- }
- }
- }
- }
- int main()
- {
- scanf("%d",&n);
- prime();
- for(int i=3;i<=n/2;i++)
- {
- if(!p[i] || vis[i])continue;
- int sum=0;
- for(int j=1;j<=n/i;j++)if(!vis[i*j])sum++;
- if(sum%2==0)
- {
- for(int j=1;j<=n/i;j++)
- {
- if(j+1>n/i)break;
- if(vis[i*j])
- {
- continue;
- }
- else if(vis[i*(j+1)])
- {
- int k;
- for(k=j+2;k<=n/i;k++)
- {
- if(!vis[i*k])
- {
- v.push_back(make_pair(j*i,i*k));
- vis[j*i]=vis[i*k]=1;
- ++cnt;
- break;
- }
- }
- j=k;
- continue;
- }
- v.push_back(make_pair(j*i,i*(j+1)));
- vis[j*i]=vis[i*(j+1)]=1;
- j++;
- ++cnt;
- }
- }
- else
- {
- for(int j=1;j<=n/i;j++)
- {
- if(j+1>n/i)break;
- if(j==2)continue;
- if(vis[i*j])
- {
- continue;
- }
- else if(vis[i*(j+1)] || j+1==2)
- {
- int k;
- for(k=j+2;k<=n/i;k++)
- {
- if(!vis[i*k])
- {
- v.push_back(make_pair(j*i,i*k));
- vis[j*i]=vis[i*k]=1;
- ++cnt;
- break;
- }
- }
- j=k;
- continue;
- }
- v.push_back(make_pair(j*i,i*(j+1)));
- vis[j*i]=vis[i*(j+1)]=1;
- j++;
- ++cnt;
- }
- }
- }
- for(int i=1;i<=n/2;i++)
- {
- if(i+1>n/2)break;
- if(vis[i*2])continue;
- else if(vis[2*(i+1)])
- {
- int j;
- for(j=i+2;j<=n/2;j++)
- {
- if(!vis[2*j])
- {
- v.push_back(make_pair(2*i,2*j));
- vis[2*i]=vis[2*j]=1;
- ++cnt;
- break;
- }
- }
- i=j;
- continue;
- }
- v.push_back(make_pair(2*i,2*i+2));
- vis[2*i]=vis[2*(i+1)]=1;
- i++;
- ++cnt;
- }
- printf("%d\n",cnt);
- for(int i=0;i<cnt;i++)
- {
- printf("%d %d\n",v[i].first,v[i].second);
- }
- return 0;
- }
Codeforces Round #257 (Div. 1)A~C(DIV.2-C~E)题解的更多相关文章
- 【Codeforces Round 1129】Alex Lopashev Thanks-Round (Div. 1)
Codeforces Round 1129 这场模拟比赛做了\(A1\).\(A2\).\(B\).\(C\),\(Div.1\)排名40. \(A\)题是道贪心,可以考虑每一个站点是分开来的,把目的 ...
- Codeforces Round #257 (Div. 1) C. Jzzhu and Apples (素数筛)
题目链接:http://codeforces.com/problemset/problem/449/C 给你n个数,从1到n.然后从这些数中挑选出不互质的数对最多有多少对. 先是素数筛,显然2的倍数的 ...
- Codeforces Round #257 (Div. 2) B. Jzzhu and Sequences (矩阵快速幂)
题目链接:http://codeforces.com/problemset/problem/450/B 题意很好懂,矩阵快速幂模版题. /* | 1, -1 | | fn | | 1, 0 | | f ...
- Codeforces Round #257 (Div. 1)449A - Jzzhu and Chocolate(贪婪、数学)
主题链接:http://codeforces.com/problemset/problem/449/A ------------------------------------------------ ...
- Codeforces Round #257 (Div. 2) A. Jzzhu and Children(简单题)
题目链接:http://codeforces.com/problemset/problem/450/A ------------------------------------------------ ...
- Codeforces Round #257(Div. 2) B. Jzzhu and Sequences(矩阵高速幂)
题目链接:http://codeforces.com/problemset/problem/450/B B. Jzzhu and Sequences time limit per test 1 sec ...
- Codeforces Round #257 (Div. 2)
A - Jzzhu and Children 找到最大的ceil(ai/m)即可 #include <iostream> #include <cmath> using name ...
- Codeforces Round #257(Div.2) D Jzzhu and Cities --SPFA
题意:n个城市,中间有m条道路(双向),再给出k条铁路,铁路直接从点1到点v,现在要拆掉一些铁路,在保证不影响每个点的最短距离(距离1)不变的情况下,问最多能删除多少条铁路 分析:先求一次最短路,铁路 ...
- Codeforces Round #257 (Div. 2) B
B. Jzzhu and Sequences time limit per test 1 second memory limit per test 256 megabytes input standa ...
随机推荐
- 多机并行计算框架 和CoolHash数据库(可用于多机机器学习)
http://my.oschina.net/fourinone/blog/289122 http://www.oschina.net/p/fourinone
- Oracle使用rowid删除重复记录
/**如何删除重复记录?*//*1. 先按重复字段分组 2. 在每组里找出最小的rowid 3. 把整个表中与上面查询出来的rowid不相等的记录删除掉*/delete from test_t ...
- 多年心愿,终于完成,热泪盈眶啊。。。Adrew NG 的 机器学习
谢谢Andrew老师!谢谢Coursera!谢谢自己!希望这是一个好的开始!希望自己也能使用机器学习来make a better world...
- openstack controller ha测试环境搭建记录(十五)——创建实例
# source demo-openrc.sh # ssh-keygenGenerating public/private rsa key pair.Enter file in which to sa ...
- OC语言的特性(一)-消息传递与调用函数的表现形式
我们在初学Objective-C时,都会觉得ObjC中的消息传递和其他语言的调用函数差不多,只是在OC中,方法调用用消息传递这一概念来代替. 那么到底怎样区别OC中的消息传递与其他语言的调用函数呢. ...
- HMM 隐马尔科夫模型
参考如下博客: http://www.52nlp.cn/itenyh%E7%89%88-%E7%94%A8hmm%E5%81%9A%E4%B8%AD%E6%96%87%E5%88%86%E8%AF%8 ...
- 【亲测】Python:解决方案:Python Version 2.7 required, which was not found in the registry
好久不更新随笔了,今天因为数据可视化作业,想抓取一些人人网好友关系数据,于是开始尝试python,用到numpy模块,安装的时候提示: 'Python Version 2.7 required, wh ...
- iOS-模糊查询
http://blog.csdn.net/qq_33701006/article/details/51836914 版权声明:本文为博主原创文章,未经博主允许不得转载. 目录(?)[+] 前言 ...
- LPC1768外部中断与GPIO中断
LPC1768的外部中断严格来说只有四个,分别是EINT0,EINT1,EINT2,EINT3,技术手册上有如下说明 控制这四个外部中断靠以下寄存器 这三个寄存器的0 1 2 3位分别代表中断的0 1 ...
- mybatis--常见的错误
1.没有在configuration.xml配置对应的sql配置文件 错误: Error updating database. Cause: java.lang.IllegalArgumentExce ...
