DFT 展开式和 FFT推导

C语言的FFT

//----------------------------------------------------------------------------------

//----------------------------------------------------------------------------------

01.void      dft()  
02.{  
03.          extern int     inv;  
04.          extern long    npt;  
05.          long           k,n;  
06.          double         WN,wk,c,s,XR[size],XI[size];  
07.          extern complex x[size];  
08.  
09.          WN=2*pi/npt;  
10.  
11.          if(inv==1)  
12.              WN=-WN;  
13.  
14.          for(k=0;k<npt;++k)  
15.          {  
16.              XR[k]=0.0;XI[k]=0.0;  
17.              wk=k*WN;  
18.  
19.              for(n=0;n<npt;++n)  
20.              {  
21.                    c=cos(n*wk);s=sin(n*wk);  
22.                    XR[k]=XR[k]+x[n+1].real*c+x[n+1].imag*s;  
23.                    XI[k]=XI[k]-x[n+1].real*s+x[n+1].imag*c;  
24.              }  
25.              if(inv==1)  
26.              {  
27.                XR[k]=XR[k]/npt;   
28.                XI[k]=XI[k]/npt;  
29.              }  
30.          }  
31.  
32.          for(k=1;k<=npt;++k)  
33.          {  
34.              x[k].real=XR[k-1];  
35.              x[k].imag=XI[k-1];  
36.          }  
37.  
38.}

//----------------------------------------------------------------------------------

//----------------------------------------------------------------------------------

离散DFT 的展开式子

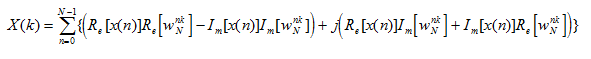
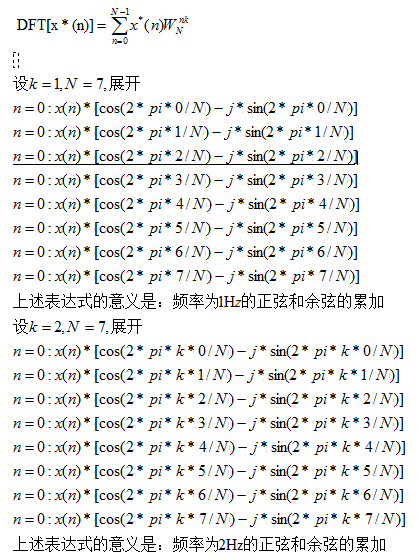
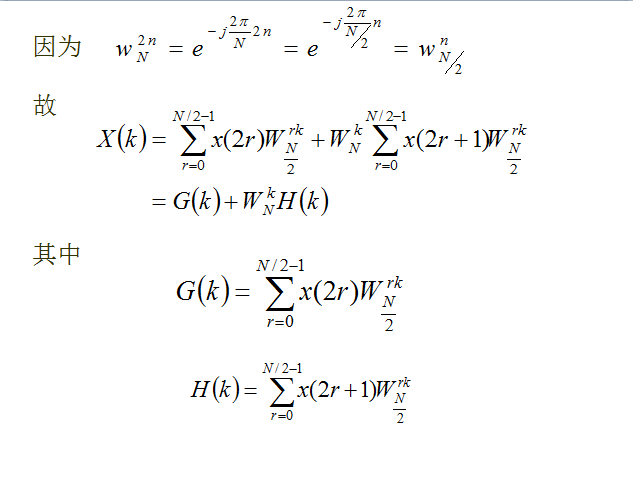
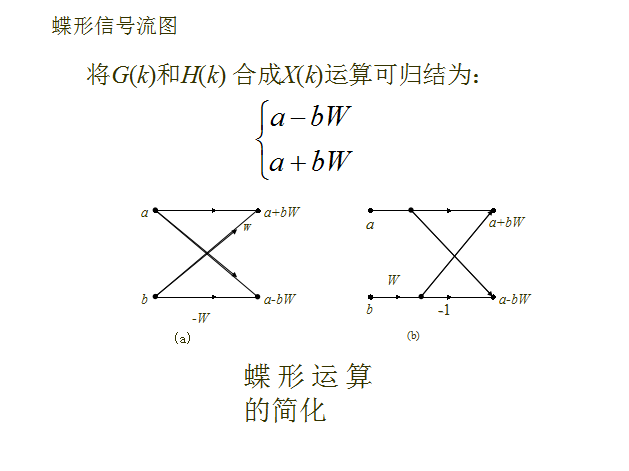
图 (a)为实现这一运算的一般方法，它需要两次乘法、两次加减法。考虑到-bW和bW两个乘法仅相差一负号，可将图 (a)简化成图2.7(b)，此时仅需一次乘法、两次加减法。图 (b)的运算结构像一蝴蝶通常称作蝶形运算结构简称蝶形结，采用这种表示法，就可以将以上所讨论的分解过程用流图表示。

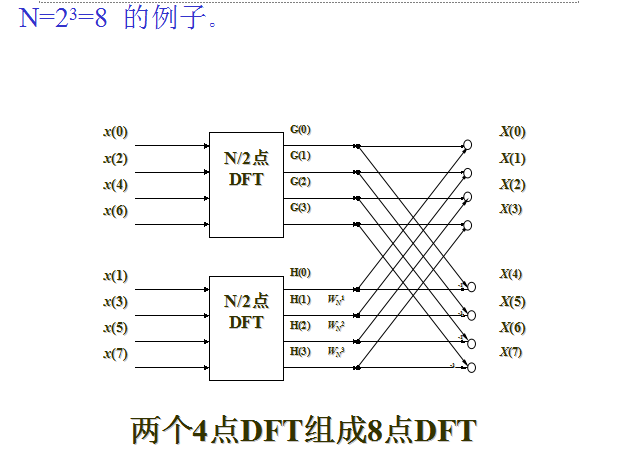
按照这个办法，继续把N/2用２除，由于N=2M，仍然是偶数，可以被２整除，因此可以对两个N/2点的DFT再分别作进一步的分解。即对{G(k)}和{H(k)}的计算，又可以分别通过计算两个长度为N/4=2点的DFT，进一步节省计算量，见图。这样，一个８点的DFT就可以分解为四个２点的DFT。

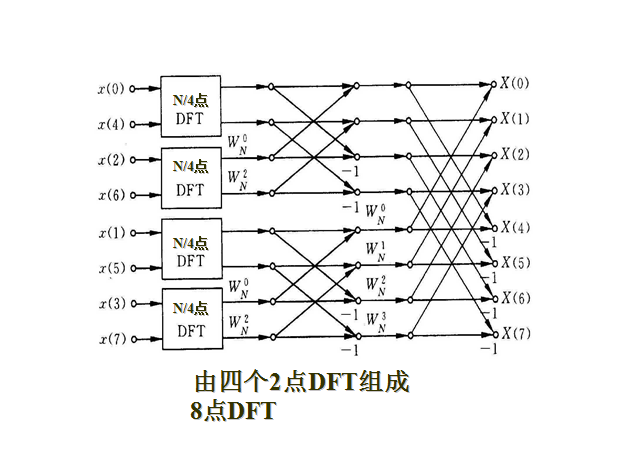
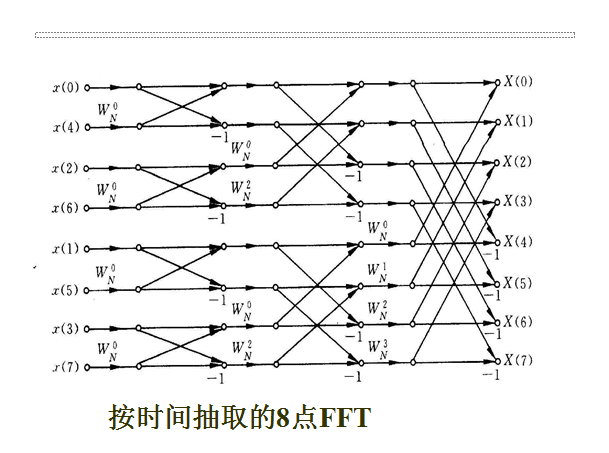
如果用反推法，把上图的蝶形运算FFT，展开求出X(0)，其结果和DFT的结果完全一致。