洛谷 P1053 逛公园 解题报告

P3953 逛公园

问题描述

策策同学特别喜欢逛公园。 公园可以看成一张\(N\)个点\(M\)条边构成的有向图，且没有自环和重边。其中1号点是公园的入口，\(N\)号点是公园的出口，每条边有一个非负权值，代表策策经过这条边所要花的时间。

策策每天都会去逛公园，他总是从1号点进去，从\(N\)号点出来。策策喜欢新鲜的事物，他不希望有两天逛公园的路线完全一样，同时策策还是一个特别热爱学习的好孩子，他不希望每天在逛公园这件事上花费太多的时间。如果1号点到\(N\)号点的最短路长为\(d\)，那么策策只会喜欢长度不超过\(d+K\)路线。

策策同学想知道总共有多少条满足条件的路线，你能帮帮他吗？

为避免输出过大，答案对P取模。

如果有无穷多条合法的路线，请输出−1。

输入格式

第一行包含一个整数\(T\)，代表数据组数。

接下来\(T\)组数据，对于每组数据：

第一行包含四个整数\(N,M,K,P\)每两个整数之间用一个空格隔开。

接下来M行，每行三个整数\(a_i,b_i,c_i\)，代表编号为\(a_i,b_i\)的点之间有一条权值为\(c_i\)的有向边，每两个整数之间用一个空格隔开。

输出格式

输出文件包含\(T\)行，每行一个整数代表答案。

数据规模与约定

对于不同的测试点， 我们约定各种参数的规模不会超过如下

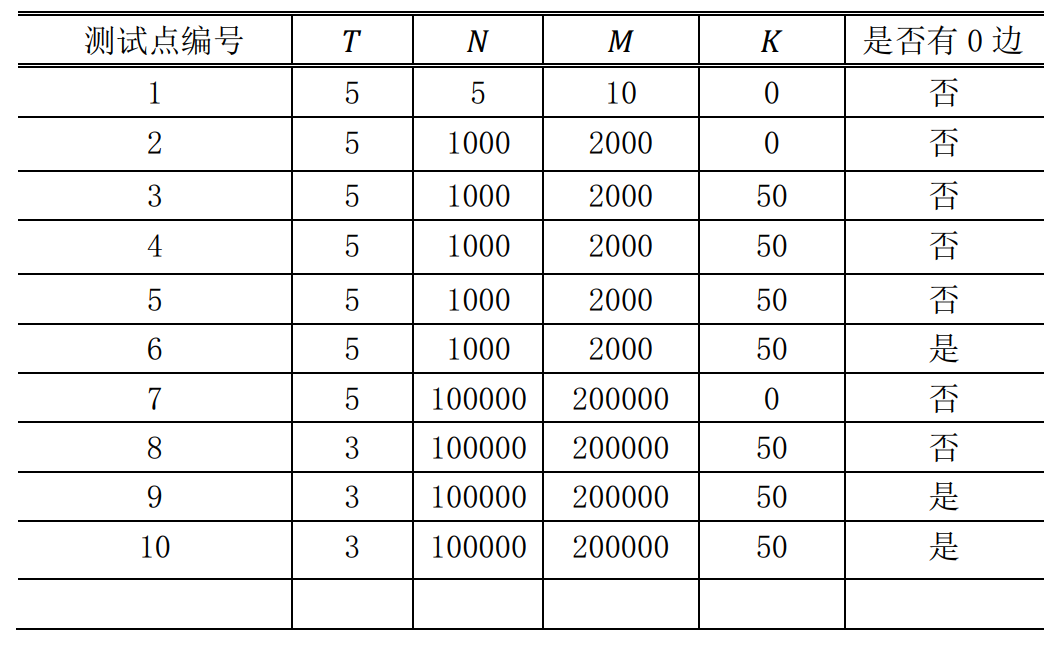
对于 100%的数据, \(1\le P \le 10^9,1\le a_i,b_i \le N, 0\le c_i \le 1000\)。

数据保证：至少存在一条合法的路线。

---

记忆化搜索真是太优雅了，除了需要判一下第0层过1点的边

正题：

其实基本应该都可以猜到正解的复杂度应该是\(O(NKT)\)的

有向图代表我们可以按一定的顺序进行\(DP\)

而边权又都是整数，妥妥的把多走的路\(k\)和节点压进状态转移方程

我们先不考虑0环

\(dp[i][j]\)代表在点\(j\)时多走\(i\)的路程的方案数。

为什么特意把\(i\)放在第一维？因为\(i\)相当于那个大的循环，把\(i\)做完了才做\(i+1\)

这和平常不建多层图的分层图（即在跑最短路的时候维护\(dis[i][j]\)数组，代表\(i\)节点\(j\)层的信息）做法并不一样，因为那种分层图可以直接按权值大小来或者多次松弛

转移方程:\(dp[i][v]=\sum dp[i+dis[v]-edge[u][v]-dis[u]][u]\)

当然，我们的记忆化搜索得倒着做

我们得把每一层的\(j\)都分别做一遍，这样，正环也是没有影响的

0环呢？

我们维护一个搜索树的栈，代表这个点和深度的二元组还在搜索树中，如果这个二元组在搜索树中的时候又被访问，则存在0环。

值得一提的是，这样在第0层时是有问题的，它判不出来过1点的0环，需要特判

---

Code：

#include <cstdio>
#include <cstring>
#include <queue>
#define P pair <int,int >
using namespace std;
const int N=100010;
int head[N],edge[N<<2],to[N<<2],Next[N<<2],cnt;
void add(int u,int v,int w)
{
    edge[++cnt]=w;to[cnt]=v;Next[cnt]=head[u];head[u]=cnt;
}
int read()
{
    int x=0;char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') {x=(x<<3)+(x<<1)+c-'0';c=getchar();}
    return x;
}
int n,m,k,p,t,dp[52][N],dis[N],used[N],vis[52][N],to0[N];
priority_queue <P,vector<P >,greater <P > > q;
P p0;
void disj()
{
    memset(dis,0x3f,sizeof(dis));
    memset(used,0,sizeof(used));
    dis[1]=0;
    p0.first=0,p0.second=1;
    q.push(p0);
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(used[u]) continue;
        used[u]=1;
        for(int i=head[u];i;i=Next[i])
        {
            if(i&1) continue;
            int v=to[i],w=edge[i];
            if(dis[v]>dis[u]+w)
            {
                dis[v]=dis[u]+w;
                p0.first=dis[v],p0.second=v;
                q.push(p0);
            }
        }
    }
}
void init()
{
    memset(head,0,sizeof(head));
    cnt=1;
    n=read(),m=read(),k=read(),p=read();
    int u,v,w;
    for(int i=1;i<=m;i++)
    {
        u=read(),v=read(),w=read();
        add(u,v,w),add(v,u,w);
    }
    disj();
    memset(dp,-1,sizeof(dp));
}
int flag=0;
void dfs0(int now)
{
    vis[0][now]=1;
    for(int i=head[now];i;i=Next[i])
        if((i&1)&&!edge[i])
        {
            if(vis[0][to[i]]) {flag=1;return;}
            dfs0(to[i]);
        }
    vis[0][now]=0;
}
int dfs(int now,int rest)
{
    if(vis[rest][now]) return -1;
    if(~dp[rest][now]) return dp[rest][now];
    vis[rest][now]=1;
    int v,w,res;
    for(int i=head[now];i;i=Next[i])
    {
        if(i&1)
        {
            v=to[i],w=edge[i];
            res=dis[now]+rest-dis[v]-w;
            if(res>=0)
            {
                if(dfs(v,res)==-1) return -1;
                (dp[rest][now]+=dfs(v,res))%=p;
            }
        }
    }
    vis[rest][now]=0;
    return ++dp[rest][now];
}
void work()
{
    memset(vis,0,sizeof(vis));
    int ans=0;
    dp[0][1]=1;dfs0(1);flag=0;
    if(flag) {printf("-1\n");return;}
    for(int i=0;i<=k;i++)
    {
        dp[i][n]=dfs(n,i);
        if(!(~dp[i][n])) {printf("-1\n");return;}
        (ans+=dp[i][n])%=p;
    }
    printf("%d\n",ans);
}
int main()
{
    t=read();
    while(t--)
    {
        init();
        work();
    }
    return 0;
}

---

2018.7.10