构造Huffman以及实现

构造Huffman

题目

在作业本上分别针对权值集合W=(6,5,3,4,60,18,77)和W=(7,2,4,5,8)构造哈夫曼树，提交构造过程的照片

错误回答

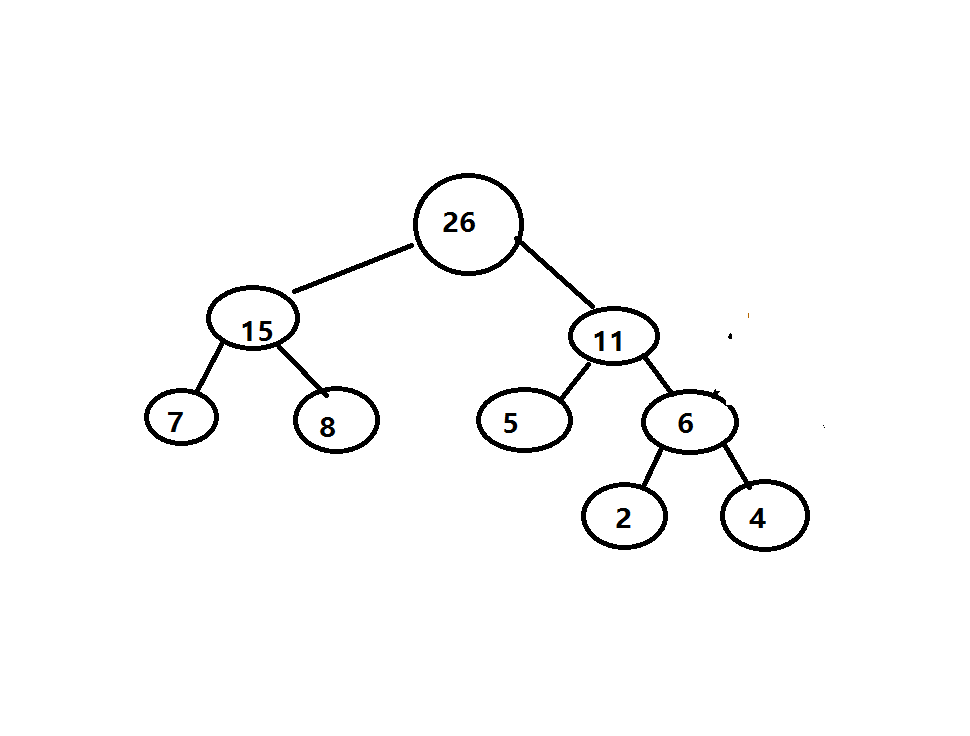
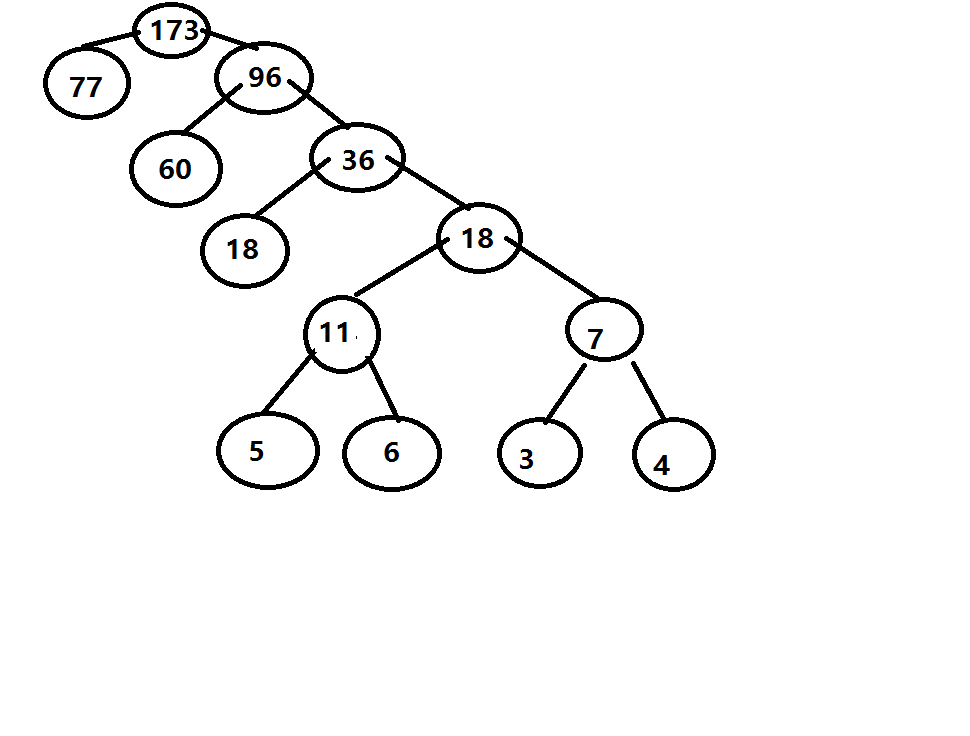
错误原因：遵循左边小于根右边大于根的原则

正确回答

HuffmanTree的实现

题目

• 1、采用静态三叉链表Triment(已经完整实现)储存HuffmanTree
• 2、理解HuffmanTree的构造过程，不中代码完成decode()
• 3、在HuffmanTreeTest中补充代码完成上个练习中的内容
• 4、提交补充代码和运行结果截图

压缩

//数据压缩，将text各字符转换成Huffman编码存储，返回压缩字符串
    public String encode(String text)
    {
        String compressed="";                              //被压缩的数据，以字符串显示
        for (int i=0; i<text.length(); i++)
            compressed += getCode(text.charAt(i)-'A');     //默认字符集是从A开始的n个字符
        return compressed;
    }

解压

    //数据解压缩，将压缩compressed中的0/1序列进行Huffman译码，返回译码字符串
    public String decode(String compressed)
    {
        //依次取出二进制的每一位，从树根向下搜索，1向右，0向左，
        // 到了叶子节点(命中)，退回根节点继续重复以上动作
        String uncompressed="";
        char code;

        TriElement node = huftree[huftree.length-1];
        int i=0;
        while(i<compressed.length()) {
            if(!node.isLeaf()){
                code = compressed.charAt(i);
                if (code == '0') {
                    node = huftree[node.left];
                } else {
                    node = huftree[node.right];
                }
                i++;
            }else if(node.isLeaf()){
                //找到该叶节点的data在权值数组中的位置
                int j=0;
                while(!(node.data == weights[j]))
                    j++;
                //该位置即为该叶节点对应字母在默认字符集中的位置
                uncompressed +=  charset.charAt(j);

                node = huftree[huftree.length-1];
            }
        }
        return uncompressed;
    }

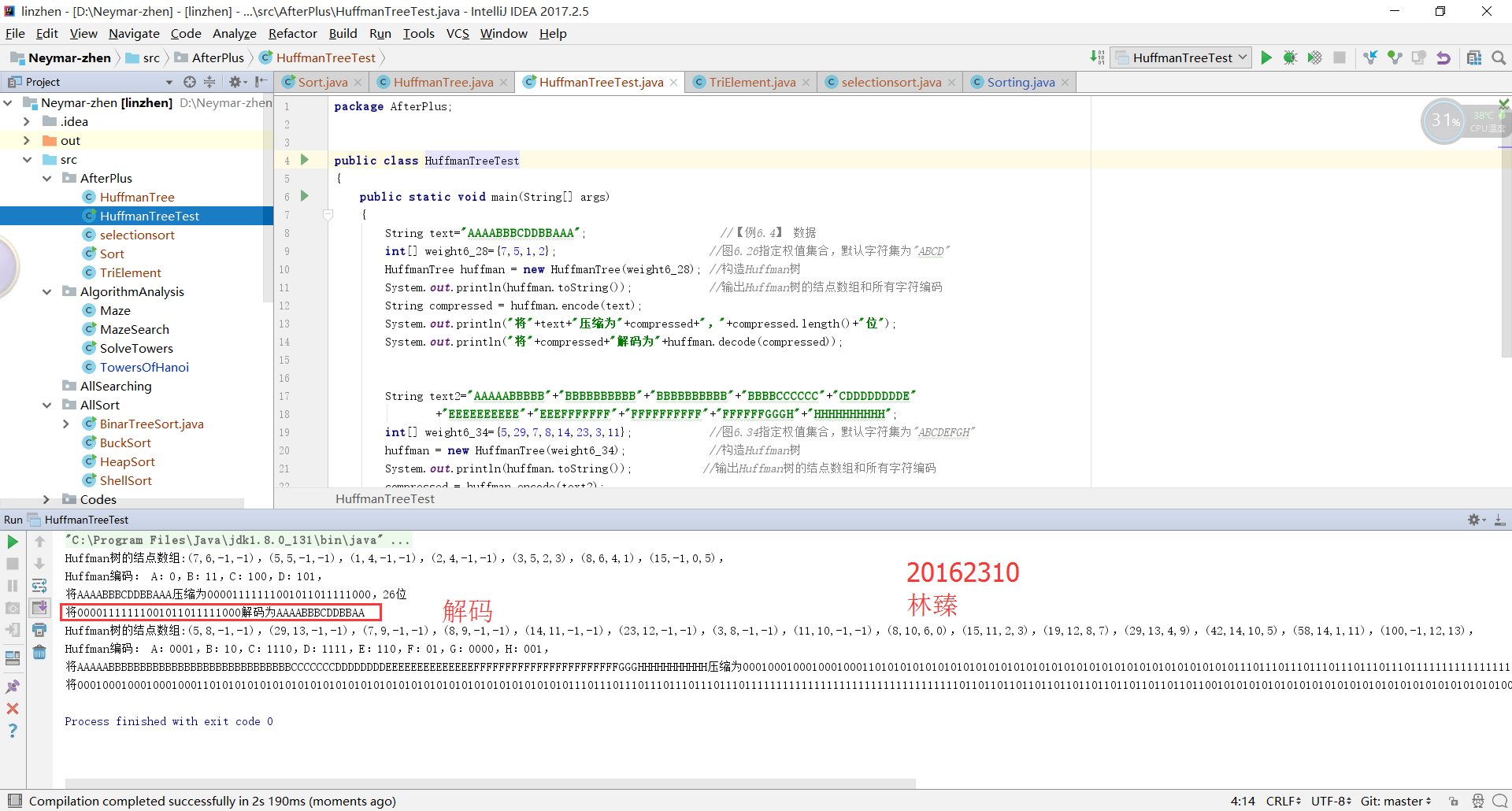
运行结果