【洛谷】4917：天守阁的地板【欧拉函数的应用】【lcm与gcd】【同除根号优化】

P4917 天守阁的地板

题目背景

在下克上异变中,博丽灵梦为了找到异变的源头,一路打到了天守阁

异变主谋鬼人正邪为了迎击,将天守阁反复颠倒过来,而年久失修的天守阁也因此掉下了很多块地板

异变结束后,恢复了正常大小的小碗回到了天守阁,想要修复这里的地板,她需要知道自己要采购的地板数量(一个惊人的数字),于是,她找到了精通oi的你来帮忙

题目描述

为了使万宝槌能发挥出全部魔力,小碗会将买来的地板铺满一个任意边长的正方形(地板有图案,因此不允许旋转,当然,地板不允许重叠)来达到最大共鸣

现在,她能够买到规格为a∗b的地板,为了省钱,她会购买尽可能数量少的地板

现在,她想知道对于每一对a,b(1≤a,b≤n),她最少需要购买的地板数量

由于输出可能很大,所以你只需要输出所有答案的乘积即可,为了避免高精度,小碗很良心的让你将答案对19260817取模

输入输出格式

输入格式：

第一行一个整数T,表示数据组数
下面T行,每行一个整数n

输出格式：

共T行,每行一个整数,表示取模后的答案

输入输出样例

输入样例#1： 复制

4
1
2
3
100

输出样例#1： 复制

1
4
1296
18996121

说明

样例解释:
对于n=1,a,b仅有(1,1)一种情况,只需要一块1∗1的地板,答案为1

对于n=2,a,b有(1,1),(1,2),(2,1),(2,2)四种情况,分别需要一块(1*1),两块(1∗2),两块(2∗1),一块(2∗2)的地板,答案为1∗2∗2∗1=4

追加解释:a,b有四种取值,分别是(1,1),(1,2),(2,1),(2,2)

当只能买到1∗1的地板时,需要一块(本身就是正方形)
当只能买到1∗2的地板时,需要两块(两块拼在一起组成2∗2的正方形)
当只能买到2∗1的地板时,需要两块(两块拼在一起组成2∗2的正方形)
当只能买到2∗2的地板时,需要一块(本身就是正方形)

答案就是这些数的乘积,即4

第一天停课的早上，在$yuli$dalao已经a掉12道题的同时，终于把这道题搞清楚了。

出题人颠覆了我对noip的看法！

抱头痛哭QAQ

题解写的确实清楚，但这这这noipd2t1考的知识点要不要太多aaa！！！欧拉函数+逆元线性筛，$gcd$和$lcm$相关公式推导，同除$O(\sqrt{n})$优化.....我大概也就到了能把第一步式子推出来的地步吧....

---

先考虑单个询问的情况,可以得到如下结论:
用$a*b$规格的地板摆成的正方形的边长最小是$lcm(a,b)$(木板不允许旋转),所以需要最小的木板数量是$\frac{lcm(a,b)}{a}*\frac{lcm(a,b)}{b}$

问题中说要把所有可能的$(a,b)$的答案求乘积,那么问题就转换成了求

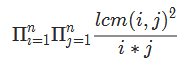
首先你必须知道

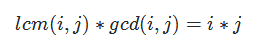
(唯一分解后易证)

因此

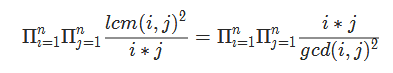
先考虑分子:

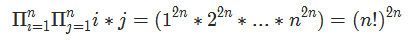
所以可以先$O(n)$预处理出阶乘$fac(i)$,用快速幂$O(logn)$算出分子

接下来考虑分母

为了方便,可以先求出

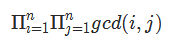
再平方

考虑枚举$d$,那么我们求出对于每个$d$有多少对$(i,j)$满足$gcd(i,j)=d$再套用快速幂即可

显然$i,j$都是$d$的倍数是必要条件,所以设$i=k_1d,j=k_2d(k1,k2≤\lfloor \frac{n}{d} \rfloor)$
那么当且仅当$gcd(k1,k2)=1$即$k1,k2$互质时符合$gcd(i,j)=d$的条件(否则$gcd$可以扩大为$d*gcd(k1,k2)$
不妨令 $k1>k2$,那么符合条件的点对数 为每个在范围内的$k1$,小于它且与它互质的数的个数的和(即$\sumφ$),所以真正的答案就是

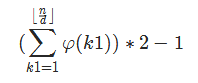
好了,到现在复杂度为$O(n+Tnlogn)$,可以拿到$60$分的好成绩(雾)

最后一个优化:
不难发现,$\lfloor \frac{n}{d} \rfloor$的取值只有$2\sqrt{n}$种,那么可以把$\lfloor \frac{n}{d} \rfloor$相等的所有d放在一起处理

假设某一段从i到j的所有数的这个值都等于x,那么这一段的乘积就等于

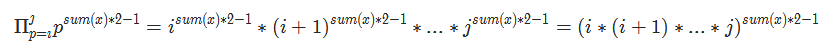
那么先预处理出$19260817$的逆元$inv(i)$,这一段的答案就是$(fac(j)*inv(fac(i-1)))^{sum(x)*2-1}$

这样处理后的最终复杂度是$O(n+T\sqrt{n}log(n))$,可以愉快的通过此题

#include<bits/stdc++.h>
#define LL long long
#define mod 19260817
#define maxn 1000000
using namespace std;

LL mpow(LL a, LL b) {
    LL ans = ;
    for(; b; b >>= , a = a * a % mod)
        if(b & )    ans = ans * a % mod;
    return ans;
}

int isnot[maxn+], prime[maxn+], t;
int fac[maxn+], inv[mod+];
LL phi[maxn+];
void init() {
    isnot[] = ; phi[] = ;
    for(int i = ; i <= maxn; i ++) {
        if(!isnot[i]) {
            prime[++t] = i;
            phi[i] = i - ;
        }
        for(int j = ; j <= t; j ++) {
            if(i * prime[j] > maxn)    break;
            isnot[i * prime[j]] = ;
            if(i % prime[j])    phi[i * prime[j]] = phi[i] * (prime[j] - );
            else {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
        }
    }
    for(LL i = ; i <= maxn; i ++)    phi[i] += phi[i-];
    fac[] = ;
    for(LL i = ; i <= maxn; i ++)    fac[i] = (LL)(fac[i-] * i) % mod;
    inv[] = inv[] = ;
    for(LL i = ; i < mod; i ++)    inv[i] = (LL)((LL)(-(mod / i) * (LL)inv[mod % i]) % mod + mod) % mod;
}

int main() {
    int T;
    scanf("%d", &T);
    init();
    while(T --) {
        int n;
        scanf("%d", &n);
        LL ans1 = mpow(fac[n],  * n);
        LL ans2 = ;
        for(LL d = , L; d <= n; d = L + ) {
            LL p = (LL) * phi[n/d] - ;
            L = n / (n / d);///////////////////////////////同除优化
            ans2 = (LL)ans2 * mpow((LL)fac[L] * (LL)inv[fac[d-]] % mod, p) % mod;
        }
        ans2 = ans2 * ans2 % mod;
        ans2 = inv[ans2];
        printf("%lld\n", ans1 * ans2 % mod);
    }
    return ;
} 

---

！！！愉快个猪皮怪物！！（不过好在复习了线性筛和一些小公式）

还有一个知识点在这里用到。

BZOJ2818:

2818: Gcd

Time Limit: 10 Sec  Memory Limit: 256 MB
Submit: 8803  Solved: 3908
[Submit][Status][Discuss]

Description

给定整数N，求1<=x,y<=N且Gcd(x,y)为素数的
数对(x,y)有多少对.

Input

一个整数N

Output

如题

Sample Input

4

Sample Output

4

HINT

hint

对于样例(2,2),(2,4),(3,3),(4,2)

1<=N<=10^7

Source

湖北省队互测

[Submit][Status][Discuss]

上面题解也有讲到，设$gcd(x,y)=d$，那么题目就是求对于每个$d$，$gcd(\frac{x}{d},\frac{y}{d})=1$的对数。设$\frac{y}{d}=k1>\frac{x}{d}=k2$，我们求$φ$的前缀和，那么就是求$φ(k1)*2-1$（$1$会多一个重复）（对于$k1=\lfloor \frac{n}{d} \rfloor$），然后枚举$d$就可以了。

这道题要求$d$是素数，所以枚举素数就行了。

#include<bits/stdc++.h>
#define LL long long
#define maxn 10000000 + 5
using namespace std;

LL phi[maxn];
int isnot[maxn], prime[maxn], n, t;

void init() {
    isnot[] = ;
    phi[] = ;
    for(int i = ; i <= n; i ++) {
        if(!isnot[i])
            prime[++t] = i, phi[i] = i - ;
        for(int j = ; j <= t; j ++) {
            int to = prime[j] * i;
            if(to > n)    break;
            isnot[to] = ;
            if(i % prime[j] == ) {
                phi[to] = phi[i] * prime[j];//////////记住就好！
                break;
            } else phi[to] = phi[i] * (prime[j] - );//////互质用积性函数的性质
        }
    }
    for(int i = ; i <= n; i ++)    phi[i] += phi[i-];
}

int main() {
    scanf("%d", &n);
    init();
    LL ans = ;
    for(int i = ; i <= t && prime[i] <= n; i ++)
        ans += (phi[n/prime[i]] *  - );
    printf("%lld", ans);
    return ;
}