详细教你实现BST(二叉排序树)

查找基本分类如下：

1. 线性表的查找

   • 顺序查找
   • 折半查找
   • 分块查找

2. 树表的查找

   • 二叉排序树
   • 平衡二叉树
   • B树
   • B+树

3. 散列表的查找

今天介绍二叉排序树。

二叉排序树 ( Binary Sort Tree ) 又称为二叉查找树，它是一种对排序和查找都很有用的特殊二叉树。

1. 二叉排序树的定义

---

二叉排序树是具有如下性质的二叉树：

1. 若它的左子树不为空，则左子树上所有节点的值均小于它的根节点的值。
2. 若它的右子树不为空，则右子树上的所有节点的值均大于它的根节点的值。
3. 它的左子树、右子树也均为二叉排序树。

二叉排序树是递归定义的。所以可以得出二叉排序树的一个重要性质：中序遍历一棵二叉排序树时可以得到一个节点值递增的有序序列。

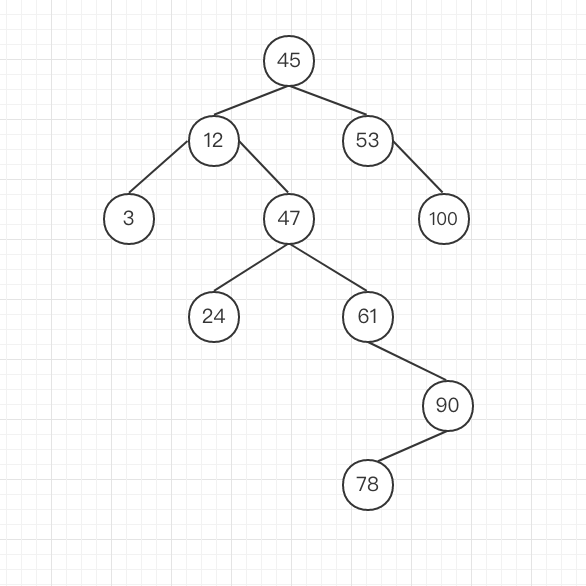
若中序遍历上图二叉树，则可以得到一个按数值大小排序的递增序列：3，12，24，37，45，53，61，78，90，100

2. 创建一个二叉排序树

---

二叉树是由节点构成，所以我们需要一个Node类，node实例保存当前节点的数据，以及保存左右节点的指针，还可以输出当前节点数据。

  class Node {
    constructor(data, leftNode, rightNode) {
      this.data = data
      this.leftNode = leftNode
      this.rightNode = rightNode
    }
    print () {
      return this.data
    }
  }

二叉排序树有一个根节点，根节点存储了根节点的数据，左右子节点的地址，还有相应的实例方法，提供插入、遍历、查找等操作。

  class BST {
    constructor() {
      this.root = null
    }

    insert (data) {...}
    preOrder () {...}
    inOrder () {...}
    postOrder () {...}
    ...
  }

3. 二叉排序树的插入

---

我们要根据二叉排序树树的性质来决定insert的data的位置

1. 若当前是一棵空树，则将插入的数据作为根节点

2. 若不是空树，循环遍历二叉排序树的节点

   • 若当前遍历的节点的data大于要插入的data，则将下一个要遍历的节点赋值为当前遍历的节点的左节点，进行下一层循环，直到叶子节点为止，将data作为叶子节点的左节点
   • 若当前遍历的节点的data小于要插入的data，则将下一个要遍历的节点赋值为当前遍历的节点的右节点，进行下一层循环，直到叶子节点为止，将data作为叶子节点的右节点

还是代码直观

  function insert (data) {
    if (this.find(data)) {
        return
    }

    var node = new Node(data, null, null)
    if (this.root == null) {
      this.root = node
    } else {
      var currentNode = this.root
      var parentNode
      while (currentNode) {
        parentNode = currentNode
        if (data < currentNode.data) {
          currentNode = currentNode.leftNode
          if (currentNode == null) {
            parentNode.leftNode = node
            break
          }
        } else {
          currentNode = currentNode.rightNode
          if (currentNode == null) {
            parentNode.rightNode = node
            break
          }
        }
      }
    }
  }

4. 递归遍历二叉排序树

---

简单，贴下代码，重点在非递归遍历

  class BST {
    constructor() {
      this.data = null
    }

    preOrder () {
      preOrderFn(this.root)
    }
    inOrder () {
      inOrderFn(this.root)
    }
    postOrder () {
      postOrderFn(this.root)
    }
  }

  function preOrderFn (node) {
    if (node) {
      console.log(node.print())
      preOrderFn(node.leftNode)
      preOrderFn(node.rightNode)
    }
  }
  function inOrderFn (node) {
    if (node) {
      inOrderFn(node.leftNode)
      console.log(node.print())
      inOrderFn(node.rightNode)
    }
  }
  function postOrderFn (node) {
    postOrderFn (node.leftNode)
    postOrderFn (node.rightNode)
    console.log(node.print())
  }

5.非递归中序遍历二叉排序树

---

中序遍历的非递归算法最简单，后序遍历的非递归算法最难，所以先介绍中序遍历。

非递归遍历一定要用到栈。

  class Stack {
    constructor() {
      this.arr = []
    }
    pop () {
      return this.arr.shift()
    }
    push (data) {
      this.arr.unshift(data)
    }
    isEmpty () {
      return this.arr.length == 0
    }
  }

我们一点一点写想，中序遍历，肯定是要先找到左子树最下面的节点吧？想不明白就好好想想。

  function inOrderWithoutRecursion (root) {
    var parentNode = root
    var stack = new Stack()

    // 一直遍历到左子树的最下面，将一路遍历过的节点push进栈中
    while (parentNode) {
      stack.push(parentNode)
      parentNode = parentNode.leftNode
    }
  }

这里为什么要先让遍历过的节点入栈呢？中序遍历，先遍历左节点，再根节点，最后是右节点，所以我们需要保存一下根节点，以便接下来访问根节点和借助根节点来访问右节点。

1.现在我们已经到了左子树的最下面的节点了，这时它是一个叶子节点。通过遍历，它也在栈中而且是在栈顶，所以就可以访问它的data了，然后访问根节点的data，最后将parentNode指向根节点的右节点，访问右节点。

如图

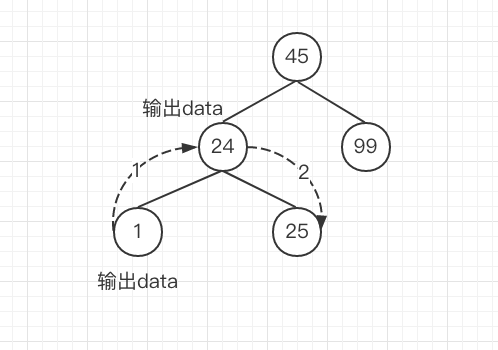
按我上面说的话，代码应该是这个样子的。

    parentNode = stack.pop()
    console.log(parentNode.data)
    parentNode = stack.pop()
    console.log(parentNode.data)
    parentNode = parentNode.rightNode

2.但是还有一种情况呢？如果左子树最下面的节点没有左节点，只有右节点呢？也就是说如果这个节点不是叶子节点呢？那么就直接访问根节点的data，再将parentNode指向根节点的右节点，访问右节点。对吧？

如图

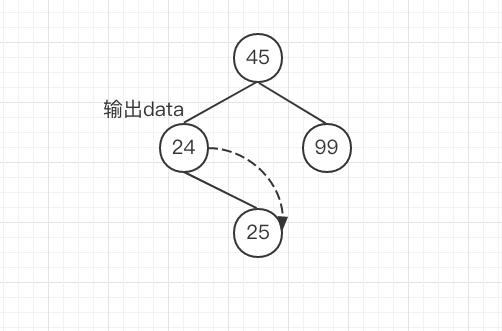
那现在代码又成了这个样子。

    parentNode = stack.pop()
    console.log(parentNode.data)
    parentNode = parentNode.rightNode

那么怎么统一格式呢？之前我们说到当parentNode不存在时就需要出栈了，那我们可以把左子树最下面的节点也就是第一种情况时的叶子节点看作一个根节点，继续访问它的右节点，因为它是一个叶子节点，所以右节点为null，所以就又执行了一次出栈操作。这时候代码就可以统一了，好好想一想，有点抽象。

统一后的代码就是情况2的代码

    parentNode = stack.pop()
    console.log(parentNode.data)
    parentNode = parentNode.rightNode

如果上面的都理解了的话，就很简单了，贴代码

  function inOrderWithoutRecursion (root) {
    if (!root)
      return

    var parentNode = root
    var stack = new Stack()

    while (parentNode || !stack.isEmpty()) {

      // 一直遍历到左子树的最下面，将一路遍历过的节点push进栈中
      while (parentNode) {
        stack.push(parentNode)
        parentNode = parentNode.leftNode
      }
      // 当parentNode为空时，说明已经达到了左子树的最下面，可以出栈操作了
      if (!stack.isEmpty()) {
        parentNode = stack.pop()
        console.log(parentNode.data)
        // 进入右子树，开始新一轮循环
        parentNode = parentNode.rightNode
      }
    }
  }

优化

  function inOrderWithoutRecursion (root) {
    if (!root)
      return

    var parentNode = root
    var stack = new Stack()

    while (parentNode || !stack.isEmpty()) {

      // 一直遍历到左子树的最下面，将一路遍历过的节点push进栈中
      if (parentNode) {
        stack.push(parentNode)
        parentNode = parentNode.leftNode
      }
      // 当parentNode为空时，说明已经达到了左子树的最下面，可以出栈操作了
      else {
        parentNode = stack.pop()
        console.log(parentNode.data)
        // 进入右子树，开始新一轮循环
        parentNode = parentNode.rightNode
      }
    }
  }

6.非递归先序遍历二叉排序树

---

有了中序遍历的基础，掌握先序遍历就不难了吧？先序就是到了根节点就打印出来，然后将节点入栈，然后左子树，基本与中序类似，想想就明白。

直接贴最终代码

  function PreOrderWithoutRecursion (root) {
    if (!root)
      return

    var parentNode = root
    var stack = new Stack()

    while (parentNode || !stack.isEmpty()) {

      // 一直遍历到左子树的最下面，一边打印data,将一路遍历过的节点push进栈中
      if (parentNode) {
        console.log(parentNode.data)
        stack.push(parentNode)
        parentNode = parentNode.leftNode
      }
      // 当parentNode为空时，说明已经达到了左子树的最下面，可以出栈操作了
      else {
        parentNode = stack.pop()
        // 进入右子树，开始新一轮循环
        parentNode = parentNode.rightNode
      }
    }
  }

7.非递归后序遍历二叉排序树

---

后序遍历中，一个根节点被访问的前提是，右节点不存在或者右节点已经被访问过

后序遍历难点在于：判断右节点是否被访问过。

• 如果右节点不存在或者右节点已经被访问过，则访问根节点

• 如果不符合上述条件，则跳过根节点，去访问右节点

我们可以使用一个变量来保存上一个访问的节点，如果是当前访问的节点的右节点就是上一个访问过的节点，证明右节点已经被访问过了，可以去访问根节点了。

这里需要注意的一点是：节点Node是一个对象，如果用==比较的话，返回的永远是false，所以我们比较的是node的data属性。

代码在这里

function PostOrderWithoutRecursion (root) {
    if (!root)
      return

    var parentNode = root
    var stack = new Stack()
    var lastVisitNode = null

    while (parentNode || !stack.isEmpty()) {
      if (parentNode) {
        stack.push(parentNode)
        parentNode = parentNode.leftNode
      }
      else {
        parentNode = stack.pop()
        // 如果当前节点没有右节点或者是右节点被访问过，则访问当前节点
        if (!parentNode.rightNode || parentNode.rightNode.data == lastVisitNode.data) {
          console.log(parentNode.data)
          lastVisitNode = parentNode
        }
        // 访问右节点
        else {
          stack.push(parentNode)
          parentNode = parentNode.rightNode
          while (parentNode) {
            parentNode = parentNode.leftNode
          }
        }
      }
    }
  }

8.二叉排序树的查找

---

写查找是为了删除节点做准备。

1.查找给定值

很简单，根据要查找的数据和根节点对比，然后遍历左子树或者右子树就好了。

  find (data) {
    var currentNode = this.root
    while (currentNode) {
      if (currentNode.data == data) {
        return currentNode
      } else if (currentNode.data > data) {
        currentNode = currentNode.leftNode
      } else {
        currentNode = currentNode.rightNode
      }
    }
    return null
  }

2.查找最大值

很简单，直接找到最右边的节点就是了

  getMax () {
    var currentNode = this.root
    while (currentNode.rightNode) {
      currentNode = currentNode.rightNode
    }
    return currentNode.data
  }

3.查找最小值

一样

  getMax () {
    var currentNode = this.root
    while (currentNode.leftNode) {
      currentNode = currentNode.leftNode
    }
    return currentNode.data
  }

9.二叉排序树的删除

---

删除很重要，说下逻辑：

首先从二叉排序树的根节点开始查找关键字为key的待删节点，如果树中不存在此节点，则不做任何操作；

否则，假设待删节点为delNode，其父节点为delNodeParent，delNodeLeft和delNodeRight分别为待删节点的左子树、右子树。

可设delNode是delNodeParent的左子树（右子树情况类似）。 分下面三种情况考虑

1.若delNode为叶子节点，即delNodeLeft和delNodeRight均为空。删除叶子节点不会破坏整棵树的结构，则只需修改delNodeParent的指向即可。

delNodeParent.leftNode = null

2.若delNode只有左子树delNodeLeft或者只有右子树delNodeRight，此时只要令delNodeLeft或者delNodeRight直接成为待删节点的父节点的左子树即可。

delNodeParent.leftNode = delNode.leftNode

（或者delNodeParent.leftNode = delNode.rightNode）

3.若delNode左子树和右子树均不为空，删除delNode之后，为了保持其他元素之间的相对位置不变，可以有两种处理办法

• 令delNode的左子树为delNodeParent的左子树，而delNode的右子树为delNode的左子树中序遍历的最后一个节点（令其为leftBigNode，即左子树中最大的节点，因为要符合二叉树的性质，仔细想一想）的右子树
  
  delNodeParent.leftNode = delNode.leftNode
  
  leftBigNode.rightNode = delNode.rightNode

• 令delNode的直接前驱（也就是左子树中最大的节点，令其为leftBigNode）替代delNode，然后再从二叉排序树中删除它的直接前驱（或直接后继，原理类似）。当以直接前驱替代delNode时，由于leftBigNode只有左子树（否则它就不是左子树中最大的节点），则在删除leftBigNode之后，只要令leftBigNode的左子树为双亲leftBigNodeParent的右子树即可。
  
  delNode.data = leftBigNode.data
  
  leftBigNodeParent.rightNode = leftBigNode.leftNode

画了三张图片来理解下：

删除节点P之前：

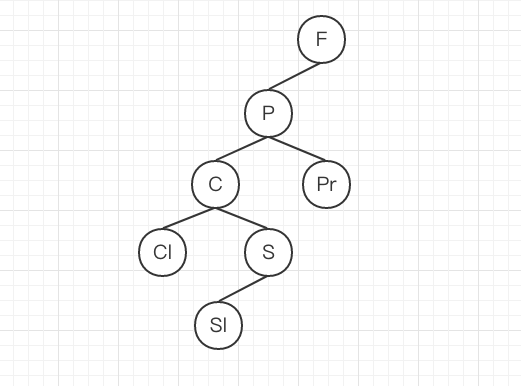
第一种方式删除后：

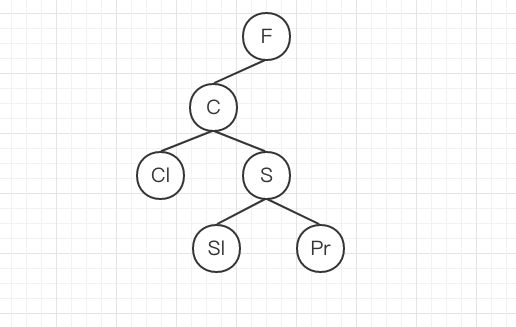
第二种方式删除后：

显然，第一种方式可能增加数的深度，而后一种方法是以被删节点左子树中最大的节点代替被删的节点，然后从左子树中删除这个节点。此节点一定没有子树（同上，否则它就不是左子树中最大的节点），这样不会增加树的高度，所以常采用这种方案，下面的算法也使用这种方案。

代码注释很清除，好好理解下，这块真的不好想

  deleteNode (data) {
    /********************** 初始化 **************************/
    var delNode = this.root,
        delNodeParent = null
    /************ 从根节点查找关键字为data的节点 ***************/
    while (delNode) {
      if (delNode.data == data) break
      delNodeParent = delNode // 记录被删节点的双亲节点
      if (delNode.data > data) delNode = delNode.leftNode // 在被删节点左子树中继续查找
      else delNode = delNode.rightNode  // 在被删节点的右子树中继续查找
    }
    if (!delNode) { // 没找到
      return
    }
    /**
     * 三种情况
     * 1.被删节点既有左子树，又有右子树
     * 2.被删节点只有右子树
     * 3.被删节点只有左子树
    **/
    var leftBigNodeParent = delNode
    if (delNode.leftNode && delNode.rightNode) { // 被删节点左右子树都存在
      var leftBigNode = delNode.leftNode
      while (leftBigNode.rightNode) { // 在被删节点的左子树中寻找其前驱节点，即最右下角的节点，也就是左子树中数值最大的节点
        leftBigNodeParent = leftBigNode
        leftBigNode = leftBigNode.rightNode // 走到右尽头
      }
      delNode.data = leftBigNode.data // 令被删节点的前驱替代被删节点
      if (leftBigNodeParent.data != delNode.data) {
        leftBigNodeParent.rightNode = leftBigNode.leftNode // 重接被删节点的前驱的父节点的右子树
      } else {
        leftBigNodeParent.leftNode = leftBigNode.leftNode // 重接被删节点的前驱的父节点的左子树
      }
    } else if (!delNode.leftNode) {
      delNode = delNode.rightNode // 若被删节点没有左子树，只需重接其右子树
    } else if (!delNode.rightNode) {
      delNode = delNode.leftNode // 若被删节点没有右子树，只需重接其左子树
    }
    /********* 将被删节点的子树挂接到其父节点的相应位置 **********/
    if (!delNodeParent) {
      this.root = delNode // 若被删节点是根节点
    } else if (leftBigNodeParent.data == delNodeParent.data) {
      delNodeParent.leftNode = delNode // 挂接到父节点的左子树位置
    } else {
      delNodeParent.rightNode = delNode // 挂接到父节点的右子树位置
    }
  }

10.其他方法

---

1.复制二叉排序树

这一块我先用了递归，后来想到，BST是个对象，直接深度克隆就好了。。。不说了

2.二叉排序树深度

递归递归递归

  class BST {
    constructor() {
      this.root = null
    }
    depth () {
      return depthFn(this.root)
    }
  }

  function depthFn (node) {
    if (!node) {
      return 0
    } else {
      var leftDepth = depthFn(node.leftNode)
      var rightDepth = depthFn(node.rightNode)
      if (leftDepth > rightDepth)
        return (leftDepth + 1)
      else
        return (rightDepth + 1)
    }
  }

3.二叉排序树节点个数

递归递归递归

  class BST {
    constructor() {
      this.root = null
    }
    nodeCount () {
      return nodeCount(this.root)
    }
  }
  function nodeCount(node) {
    if (!node) {
      return 0
    } else {
      return nodeCount(node.leftNode) + nodeCount(node.rightNode) + 1
    }
  }