统计学习方法：支撑向量机（SVM）

作者：桂。

时间：2017-05-13  21:52:14

链接：http://www.cnblogs.com/xingshansi/p/6850684.html

---

前言

主要记录SVM的相关知识，参考的是李航的《统计学习方法》，最后的SMO优化算法（Sequential minimal optimization）是二次规划的优化算法，不涉及整体思路的理解，这里打算跳过，以后用到了再来回顾。

一、线性可分支撑向量机

　　A-问题分析

不同于感知器Perceptron，SVM希望所有点到分离面的最小距离最大化，而距离分离面最近的样本点就是支撑向量（support vector）：

样本点到分离面的距离：

定义最小间隔：

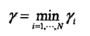
最小间隔最大化就是如下的优化问题：

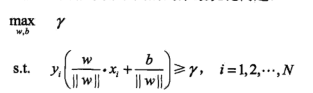
令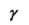=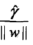，则优化问题改写为：

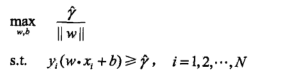
事实上的取值不影响最终的最优解，进一步转化优化问题：

这就成了一个凸二次规划（convex quadratic programming）问题了，满足凸优化的形式，可以借助对偶简化求解。

引进拉格朗日乘子：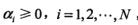

原始问题为极小极大问题，转化问对偶就是极大极小问题：

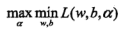
先极小求解，上述优化问题可以简化为：

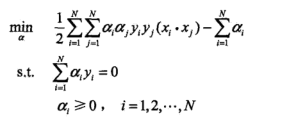
根据KKT条件，上述解对应原问题的解：

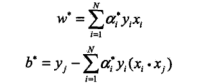
从而完成求解。

 　  B-算法步骤

　　C-应用举例

只不过这里不是求解感知器，而是SVM。

第一步：对偶问题求解

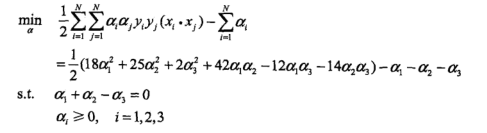求出的最优解（a1,a2）是，但a2 = -1不满足约束a2>=0，所以最小值在边界取得。

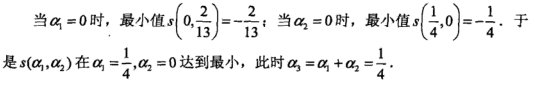
第二步：计算w与b

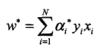=1/4*[3, 3]*1+1/4*[1, 1]*(-1)=[1/2, 1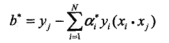/2]

=-2

第三步：得出分离决策面

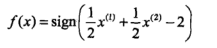
二、线性不可分情况

　　A-问题分析

其实它是对线性可分的推广，对线性可分的情况仍然适用。对于线性不可分的解决办法就是引入松弛变量，也就是加入了误差扰动：

引入松弛变量优化时考虑两方面：1）最小距离尽可能大; 2）误分类点个数尽量小。得出新的准则函数：

仍然借助对偶问题求解（剩下的思路与线性可分问题的求解思路完全一致）：

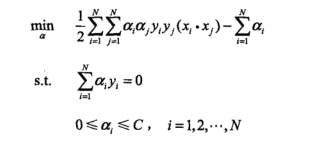
进一步得到原始问题的解：

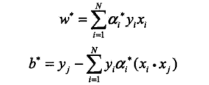
从而完成求解。

　　B-准则函数补充

因为超平面都是可以伸缩的，假设全部正确分类：

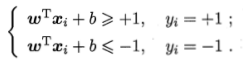
最小间隔：

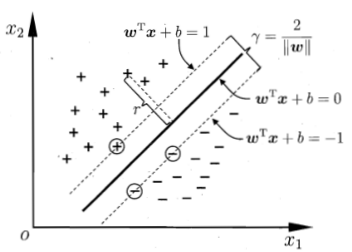
这是硬间隔，但实际中可能不能完全线性分开：

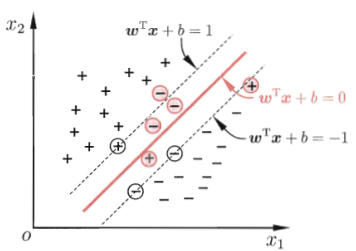
这个时候就是软间隔，即允许部分数据不满足：

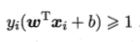
当然最大化间隔时，希望不满足条件的样本点数尽可能小，给出准则函数：

其中是0/1损失函数，用来定义不满足条件的样本数：

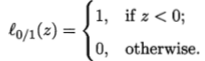
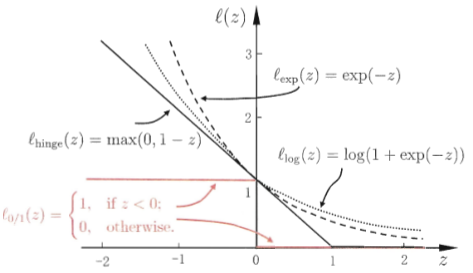
但是非凸、非连续，可以近似替代处理：

常用替代方式有三类：

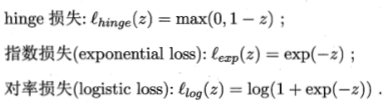
如果采用hinge损失，损失函数转化为：

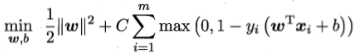
将定义为松弛变量，上式等价为：

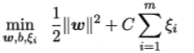
这个就是线性不可分时的准则函数了。最后回头看看近似与之间的关系：

　　C-算法步骤

给出线性支撑向量机学习算法：

三、非线性情况

关于核函数的应用，之前的文章已经分析过。

什么样的函数可以作为核函数？充要条件——K（x,z）为正定核函数：

考虑矩阵的特征值。
若所有特征值均不小于零，则称为半正定。
若所有特征值均大于零，则称为正定。

参考：

• 李航《统计学习方法》