POJ 1577Falling Leaves(二叉树的建立)

题目链接：http://poj.org/problem?id=1577

解题思路：题目是中文就不翻译了，网上都说这题很水，但本蒟蒻虽然知道是倒过来建立二叉搜索树，可是实现不了，得到小伙伴的关键递归思想的指点之后，茅塞顿开，豁然开朗，终于也能笑谈，曰之"水题"!!!

Falling Leaves

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5340		Accepted: 2886

Description

 
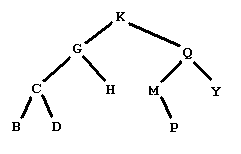
Figure 1
Figure 1 shows a graphical representation of a binary tree of letters. People familiar with binary trees can skip over the definitions of a binary tree of letters, leaves of a binary tree, and a binary search tree of letters, and go right to The problem.

A binary tree of letters may be one of two things: 

1. It may be empty.
2. It may have a root node. A node has a letter as data and refers to a left and a right subtree. The left and right subtrees are also binary trees of letters.

In the graphical representation of a binary tree of letters: 

1. Empty trees are omitted completely.
2. Each node is indicated by 
   • Its letter data,
   • A line segment down to the left to the left subtree, if the left subtree is nonempty,
   • A line segment down to the right to the right subtree, if the right subtree is nonempty.

A leaf in a binary tree is a node whose subtrees are both empty. In the example in Figure 1, this would be the five nodes with data B, D, H, P, and Y.

The preorder traversal of a tree of letters satisfies the defining properties: 

1. If the tree is empty, then the preorder traversal is empty.
2. If the tree is not empty, then the preorder traversal consists of the following, in order 
   • The data from the root node,
   • The preorder traversal of the root's left subtree,
   • The preorder traversal of the root's right subtree.

The preorder traversal of the tree in Figure 1 is KGCBDHQMPY.

A tree like the one in Figure 1 is also a binary search tree of letters. A binary search tree of letters is a binary tree of letters in which each node satisfies:

The root's data comes later in the alphabet than all the data in the nodes in the left subtree.

The root's data comes earlier in the alphabet than all the data in the nodes in the right subtree.

The problem:

Consider the following sequence of operations on a binary search tree of letters

Remove the leaves and list the data removed 
Repeat this procedure until the tree is empty 
Starting from the tree below on the left, we produce the sequence of trees shown, and then the empty tree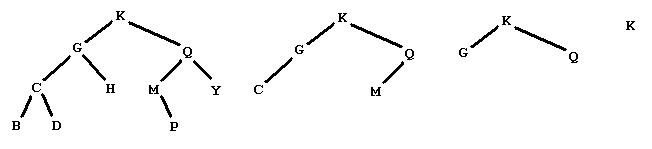 

by removing the leaves with data

BDHPY 
CM 
GQ 
K

Your problem is to start with such a sequence of lines of leaves from a binary search tree of letters and output the preorder traversal of the tree.

Input

The input will contain one or more data sets. Each data set is a sequence of one or more lines of capital letters.

The lines contain the leaves removed from a binary search tree in the stages described above. The letters on a line will be listed in increasing alphabetical order. Data sets are separated by a line containing only an asterisk ('*').

The last data set is followed by a line containing only a dollar sign ('$'). There are no blanks or empty lines in the input.

Output

For each input data set, there is a unique binary search tree that would produce the sequence of leaves. The output is a line containing only the preorder traversal of that tree, with no blanks.

Sample Input

BDHPY
CM
GQ
K
*
AC
B
$

Sample Output

KGCBDHQMPY
BAC

代码：

#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
int n;
char a[];
struct node
{
    int l,r;
    char f;
}tree[];
void Build_Tree(int index,char str)
{
    if(tree[index].f==) //虽然f是char类型，但是还是有对应的ASCII值，所以能初始化0
    {
        tree[index].f=str;
        return ;
    }
    else if(tree[index].f<str)  //由题意可得大的在右边
    {
        if(!tree[index].r)   tree[index].r=n++;
        Build_Tree(tree[index].r,str);
    }
    else
    {
        if(!tree[index].l) tree[index].l=n++;
        Build_Tree(tree[index].l,str);
    }
}
void Printf(int root)
{
    if(!tree[root].f)  return ;
    //因为题目求的是先序输出，所以这样排，交换后三句位置就是不同顺序遍历
    //先序输出，根左右，恩，就是这样
    printf("%c",tree[root].f);
    if(tree[root].l)  Printf(tree[root].l);
    if(tree[root].r)  Printf(tree[root].r);
}
int main()
{
    while(~scanf("%s",a))
    {
        char x;  n=;
        int len=strlen(a);
        memset(tree,,sizeof(tree));
        while()
        {
            scanf("%c",&x);
            if(x>='A'&&x<='Z') a[len++]=x;
            if(x=='*'||x=='$')  break;
        }
        //反过来建树
        for(int i=len-; i>=; i--)  Build_Tree(,a[i]);
        Printf();
        cout<<endl;
        if(x=='$')  break;
    }
    return ;
}