【UOJ】#37. 【清华集训2014】主旋律

题解

一道，神奇的题= =

我们考虑正难则反，我们求去掉这些边后有多少图不是强连通的

怎么求呢，不是强连通的图缩点后一定是一个DAG，并且这个DAG里面有两个点

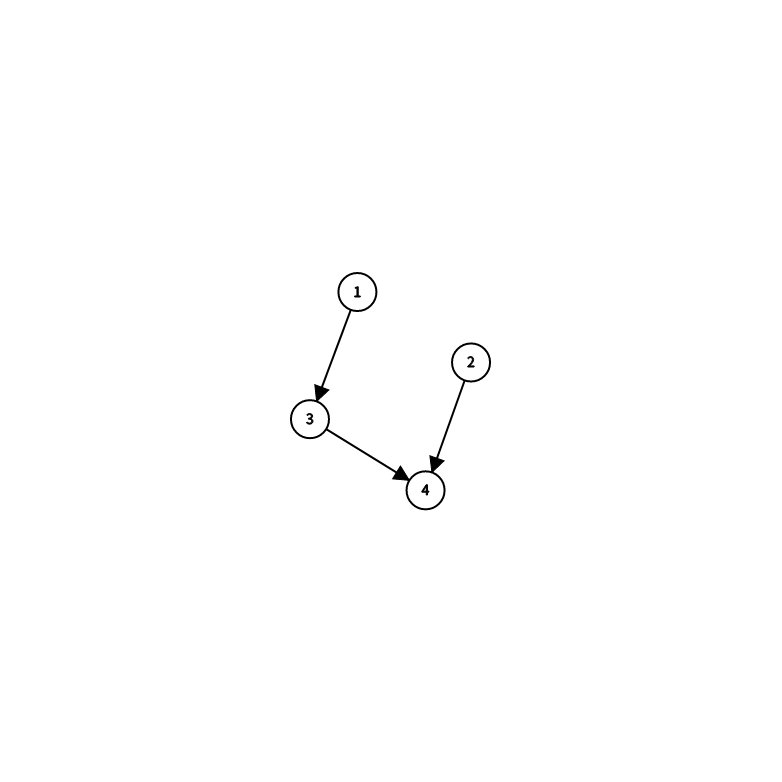
我们想一下，如果我们把1当成入度为0的点，随便造出个图，可以是这个图吧

如果把2当成入度为0的点，随便造出个图，也可以是这个图吧

把1和2当成入度为0的点，随便造出个图，还可以是这个图吧……

那么这像什么，容斥啊

以下的点说的都是缩点后的点

奇数个入度为0的点就是+，偶数个入度为0的点就是-

那么我们就有了一个精妙的容斥！

设\(f[S]\)为点集S是强连通分量的方案数

设\(g[S]\) ……是……

定义可能很奇怪，是容斥出来的，点集S的系数

嗯，这么考虑，我们知道了S这个点全是入度为0的点，那么剩下的造图的过程，就是S这个点集向外延伸的边，和除S中的点之外的点之间的边，有或没有，乘上一个2的指数幂就好

那么，怎么知道S这个系数呢？？？

我们考虑S中包含一个编号最小的点u的强连通分量，且入度为0

假如这个点的集合是T，T包含u

那么\(g[S] = g[S] - g[S ^ T] * f[T]\)，咦，为什么是减法

因为\(g[S ^ T]\)容斥的系数，在多了一个联通块后，所有的奇偶性都改变了，那么+-号也取反了，所以是减法

最后，我们用每个S的子集（包括S）算一遍不合法的图，用总共的图减掉就行，就是\(f[S]\)的值

还有\(g[S] += f[S]\)这样的话，代表整个S是一个强连通分量，S缩点后构成的入度为0的点是1个

\(h[S]\)表示S这个点集中的边

\(w[T]\)表示在全集是S的情况下，选择T这个点集作为缩点后入度为0的点，能向外延伸的边集

代码

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
//#define ivorysi
#define pb push_back
#define space putchar(' ')
#define enter putchar('\n')
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define mo 974711
#define MAXN 100005
#define RG register
using namespace std;
typedef long long int64;
typedef double db;
template<class T>
void read(T &res) {
    res = 0;char c = getchar();T f = 1;
    while(c < '0' || c > '9') {
	if(c == '-') f = -1;
	c = getchar();
    }
    while(c >= '0' && c <= '9') {
	res = res * 10 + c - '0';
	c = getchar();
    }
    res *= f;
}
template<class T>
void out(T x) {
    if(x < 0) {putchar('-');x = -x;}
    if(x >= 10) {
	out(x / 10);
    }
    putchar('0' + x % 10);
}
const int MAXS = 1 << 15;
const int MOD = 1000000007;
int N,M;
int cnt[MAXS + 5],In[MAXS + 5],Out[MAXS + 5],h[MAXS + 5],w[MAXS + 5],g[MAXS + 5],f[MAXS + 5],pow2[405];
inline int inc(int a,int b) {a = a + b;if(a >= MOD) a -= MOD;return a;}
inline int mul(int a,int b) {return 1LL * a * b % MOD;}
void Init() {
    read(N);read(M);
    pow2[0] = 1;
    for(int i = 1 ; i <= M ; ++i) {
	pow2[i] = pow2[i - 1] << 1;
	if(pow2[i] >= MOD) pow2[i] -= MOD;
    }
    for(int i = 1 ; i < MAXS ; ++i) cnt[i] = cnt[i - (i & -i)] + 1;
    int u,v;
    for(int i = 1 ; i <= M ; ++i) {
	read(u);read(v);--u;--v;
	In[1 << v] |= 1 << u;
	Out[1 << u] |= 1 << v;
    }
}
void Solve() {
    for(int S = 1 ; S < (1 << N) ; ++S) {
	if(cnt[S] == 1) {
	    h[S] = 0;f[S] = g[S] = 1;
	    continue;
	}
	int v = S & (-S);
	h[S] = h[S ^ v] + cnt[In[v] & S] + cnt[Out[v] & S];
	for(int T = (S - 1) & S ; T ; T = (T - 1) & S) {
	    if(T & v) {
		g[S] = inc(g[S],MOD - mul(g[S ^ T],f[T]));
	    }
	}
	int rev_f = 0;
	for(int T = S ; T ; T = (T - 1) & S) {
	    if(T == S) w[T] = 0;
	    else {
		v = (S ^ T) & -(S ^ T);
		w[T] = w[T ^ v] - cnt[Out[v] & (S ^ T)] + cnt[In[v] & T];
	    }
	    rev_f = inc(rev_f,mul(g[T],pow2[h[S ^ T] + w[T]]));
	}
	f[S] = inc(pow2[h[S]],MOD - rev_f);
	g[S] = inc(g[S],f[S]);
    }
    out(f[(1 << N) - 1]);enter;
}
int main() {
#ifdef ivorysi
    freopen("f1.in","r",stdin);
#endif
    Init();
    Solve();
    return 0;
}