算法笔记_067:蓝桥杯练习 算法训练 安慰奶牛（Java）

目录

1 问题描述

2 解决方案

 

---

1 问题描述

问题描述

Farmer John变得非常懒，他不想再继续维护供奶牛之间供通行的道路。道路被用来连接N个牧场，牧场被连续地编号为1到N。每一个牧场都是一个奶牛的家。FJ计划除去P条道路中尽可能多的道路，但是还要保持牧场之间 的连通性。你首先要决定那些道路是需要保留的N-1条道路。第j条双向道路连接了牧场Sj和Ej(1 <= Sj <= N; 1 <= Ej <= N; Sj != Ej)，而且走完它需要Lj的时间。没有两个牧场是被一条以上的道路所连接。奶牛们非常伤心，因为她们的交通系统被削减了。你需要到每一个奶牛的住处去安慰她们。每次你到达第i个牧场的时候(即使你已经到过)，你必须花去Ci的时间和奶牛交谈。你每个晚上都会在同一个牧场(这是供你选择的)过夜，直到奶牛们都从悲伤中缓过神来。在早上 起来和晚上回去睡觉的时候，你都需要和在你睡觉的牧场的奶牛交谈一次。这样你才能完成你的 交谈任务。假设Farmer John采纳了你的建议，请计算出使所有奶牛都被安慰的最少时间。

输入格式

第1行包含两个整数N和P。

接下来N行，每行包含一个整数Ci。

接下来P行，每行包含三个整数Sj, Ej和Lj。

输出格式

输出一个整数, 所需要的总时间(包含和在你所在的牧场的奶牛的两次谈话时间)。

样例输入

5 7
10
10
20
6
30
1 2 5
2 3 5
2 4 12
3 4 17
2 5 15
3 5 6

样例输出

176

数据规模与约定

5 <= N <= 10000，N-1 <= P <= 100000，0 <= Lj <= 1000，1 <= Ci <= 1,000。

---

2 解决方案

首先说一下这个题目的问题以及题意的理解：

问题：

题目给出的输入样例数据，其中顶点数为5，边数为7，可是样例数据中的实际只有6条边的数据，这个有点坑啊...，后来提交代码，看了一下第一组测试数据，这组数据就是样例数据，其第7条边数据为 4  5  7。

期题意中样例输入输出数据应为：

样例输入

5 7
10
10
20
6
30
1 2 5
2 3 5
2 4 12
3 4 17
2 5 15
3 5 6

4 5 12

样例输出

176

题意理解：初步读这题，为了理解题意也是读了三四遍，其中：你每个晚上都会在同一个牧场(这是供你选择的)过夜，直到奶牛们都从悲伤中缓过神来。这句话我也是醉了，为了描述一个题目，也不要弄得这么文艺呀。该题传到意思核心：即首先找到n个牧场的最小生成树，然后，选择其中一个开始进行遍历，最后要回到起点点牧场。

分析到这里，大家要注意，这里有一个小坑，那就是怎么寻找最小生成树？即是直接使用牧场之间的距离行走时间Lj来确定最小生成树，还是要把每个牧场交谈时间Ci也算入最小生成树的判断？

我刚开始做的时候，是使用Li来确定最小生成树，然后选择其中Ci最小的牧场开始出发，最后回到出发点，会发现对于题目中所给的样例输入数据测试，其输出为178，而不是题目中的176。

然后，我经过检查发现2 4 12，4 5 12这两条边选择不同其最终的输出样例也不同，顶点2的Ci为10，顶点5的Ci为30，然后自己测试了一次，如果最小生成树选择4 5 12，样例输出为178，如果选择2 4  12样例输出为176。这里面影响的原因就是构造的最小生成树不对。

所以，到了这里我们再分析一下，从顶点1到顶点2所耗费时间为2*L12 + C1 + C2，这里为什么会有2 * L12呢？因为题意中说明从某一个牧场出发后，最终还要返回这个牧场，说明每一条边要行走2次，即一去一回。那么又有新的问题了，为什么C1和C2不乘以2呢？我们在看看最小生成树，就会发现，如果一个牧场，只有一条边连接，其顶点值计算一次，如果有2条边，就计算2次，3条边就计算3次，依次类推。那么在公式里2 * L12 + C1 + C2就很好的说明了一点，那就是一个牧场有几条边，那它的顶点就被加了几次。

这里就可以理解为顶点C1到C2的边的权值为 2*L12 + C1 + C2，然后，利用这个权值求取最小生成树。

到了这里问题已经解决了百分之九十五了，最后，再选择一个牧场顶点Ci最小的值，用这么最小Ci加上最小生成树的权值和就可以得到最终的结果啦。

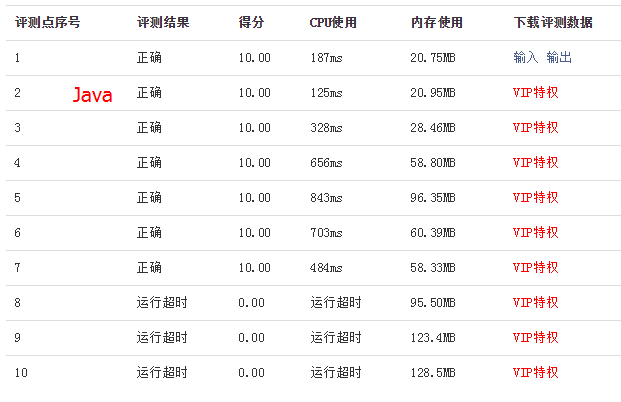
此处还有一点问题就是，下面我的代码在练习系统中的最终评分为70分，
具体原因为：运行超时。

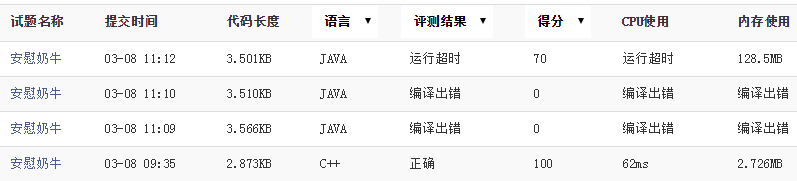
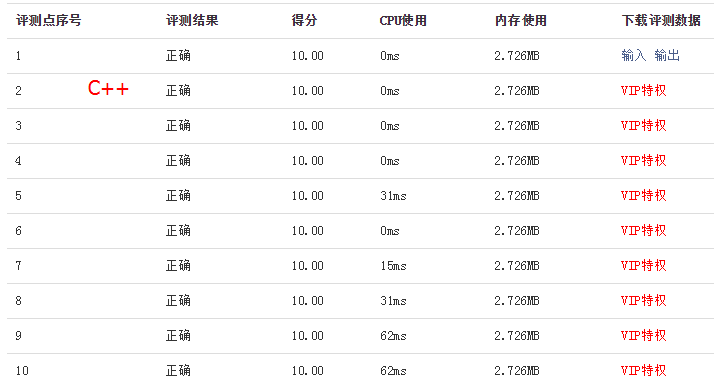
然后，我用同样方法的C语言代码在系统里运行后，测试结果为100分（PS：此处代码可以看出文末给出的参考资料）。可以看出Java和Ｃ／Ｃ＋＋运行时间有很大差异啊。（ＰＳ：如有同学路过，发现不是语言运行性能的原因，而是选用方法不当造成运行超时的话，希望不吝赐教呀～）

下面代码中，我是使用Kruskal算法实现，具体原理可以参考楼主的另一篇博客：算法笔记_066:Kruskal算法详解（Java）

具体代码如下：

import java.util.Scanner;

public class Main {

    class edge {
        public int a;
        public int b;
        public int value;

        edge(int a, int b, int value) {
            this.a = a;
            this.b = b;
            this.value = value;
        }
    }

    public void edgeSort(edge[] A){
        if(A.length > 1) {
            edge[] leftA = getHalfEdge(A, 0);
            edge[] rightA = getHalfEdge(A, 1);
            edgeSort(leftA);
            edgeSort(rightA);
            mergeEdgeArray(A, leftA, rightA);
        }
    }

    public edge[] getHalfEdge(edge[] A, int judge) {
        edge[] half;
        if(judge == 0) {
            half = new edge[A.length / 2];
            for(int i = 0;i < A.length / 2;i++)
                half[i] = A[i];
        } else {
            half = new edge[A.length - A.length / 2];
            for(int i = 0;i < A.length - A.length / 2;i++)
                half[i] = A[A.length / 2 + i];
        }
        return half;
    }

    public void mergeEdgeArray(edge[] A, edge[] leftA, edge[] rightA) {
        int i = 0;
        int j = 0;
        int len = 0;
        while(i < leftA.length && j < rightA.length) {
            if(leftA[i].value < rightA[j].value) {
                A[len++] = leftA[i++];
            } else {
                A[len++] = rightA[j++];
            }
        }
        while(i < leftA.length) A[len++] = leftA[i++];
        while(j < rightA.length) A[len++] = rightA[j++];
    }
    //获取节点a的根节点
    public int find(int[] id, int a) {
        int x, r, k;
        r = a;
        while(id[r] >= 0) r = id[r];
        k = a;
        while(k != r) {
            x = id[k];
            id[k] = r;
            k = x;
        }
        return r;
    }
    //合并a节点所在树和b节点所在树
    public void union(int[] id, int a, int b) {
        int ida = find(id, a);
        int idb = find(id, b);
        int num = id[ida] + id[idb];
        if(id[ida] < id[idb]) {
            id[idb] = ida;
            id[ida] = num;
        } else {
            id[ida] = idb;
            id[idb] = num;
        }
    }
    //获取题意最终结果
    public void getMinSpanTree(edge[] A, int[] valueN) {
        int sum = 0;
        int[] id = new int[valueN.length];

        for(int i = 0;i < valueN.length;i++)
            id[i] = -1;
        edgeSort(A);
        int count = 0;
        for(int i = 0;i < A.length;i++) {
            int a = A[i].a;
            int b = A[i].b;
            int ida = find(id, a - 1);
            int idb = find(id, b - 1);
            if(ida != idb) {
                sum += A[i].value;
                count++;
                union(id, a - 1, b - 1);
            }
            if(count >= valueN.length - 1)
                break;
        }

        int minValueN = valueN[0];
        for(int i = 0;i < valueN.length;i++) {
            if(minValueN > valueN[i]) {
                minValueN = valueN[i];
            }
        }
        sum += minValueN;
        System.out.println(sum);
    }

    public static void main(String[] args){
        Main test = new Main();
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int p = in.nextInt();
        if(n > 10000 || n < 5)
            return;
        if(p > 100000 || p < n - 1)
            return;
        int[] valueN = new int[n];
        for(int i = 0;i < n;i++)
            valueN[i] = in.nextInt();
        edge[] A = new edge[p];
        for(int i = 0;i < p;i++) {
            int a = in.nextInt();
            int b = in.nextInt();
            int value = in.nextInt() * 2 + valueN[a - 1] + valueN[b - 1];
            A[i] = test.new edge(a, b, value);
        }
        test.getMinSpanTree(A, valueN);
    }
}

参考资料：

1.算法训练 安慰奶牛（最小生成树）