Luogu P1429 平面最近点对 【分治】By cellur925

题目传送门

题目大意：给定平面上n个点，找出其中的一对点的距离，使得在这n个点的所有点对中，该距离为所有点对中最小的。$n$<=100000。

---

$Algorithm$

最朴素的$n^2$枚举肯定是不行了，我们在这个数量级只能考虑$nlogn$做法。那么与这个数量级比较相关的也就是分治了。 把整个平面分为两个部分，分别求出两个部分点对间最小的距离，之后再处理跨区域的情况。

• 分治法求解步骤： O(NlogN)  by hzwer
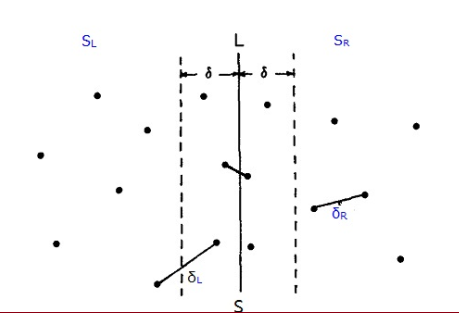
1 将点集 S 分为两个⼦集 SL 和 SR 分别求解
2 记 δ 为⼦集中求得的最优值（min(δL; δR)），合并两个集合求
解。
图中以分界线为中⼼，任何⼀个 2δ · 2δ 的正⽅形内，只有常
数个点，暴⼒ for 过去就好了。

---

$Code$

 #include<cstdio>
 #include<algorithm>
 #include<cmath> 

 using namespace std;

 int n;
 int que[];
 struct node{
     double x,y;
 }p[];
 bool cmp(node a,node b)
 {
     return a.x<b.x;
 }

 bool cmp2(int a,int b)
 {
     return p[a].y<p[b].y;
 }

 double dis(int i,int j)
 {
     return sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
 }

 double merge(int l,int r)
 {
     double dd=1e8;
     if(l==r) return dd;
     if(l+==r) return dis(l,r);
     int mid=(l+r)>>;
     double dl=merge(l,mid);
     double dr=merge(mid+,r);
     dd=min(dl,dr);

     int pos=;
     for(int i=l;i<=r;i++)
         if(fabs(p[mid].x-p[i].x)<dd) que[++pos]=i;
     sort(que+,que++pos,cmp2);
     for(int i=;i<=pos;i++)
         for(int j=i+;j<=pos;j++)
         {
             if(dis(que[i],que[j])>dd) break;
             double ddd=dis(que[i],que[j]);
             dd=min(dd,ddd);
         }
     return dd;
 }

 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
     sort(p+,p++n,cmp);
     printf("%.4lf",merge(,n));
     return ;
 }

几个注意事项

• 边界的处理。

    if(l==r) return dd;
    if(l+==r) return dis(l,r);

• 利用正方形里有常数个点的性质时，要及时$break$。否则会超时。
• 图中的$L$线大概是$mid$。开始找点的时候距离与他比较。