poj1151==codevs 3044 矩形面积求并

Atlantis

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 21511		Accepted: 8110

Description

There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.

Input

The input consists of several test cases. Each test case starts with a line containing a single integer n (1 <= n <= 100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0 <= x1 < x2 <= 100000;0 <= y1 < y2 <= 100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area. 
The input file is terminated by a line containing a single 0. Don't process it.

Output

For each test case, your program should output one section. The first line of each section must be "Test case #k", where k is the number of the test case (starting with 1). The second one must be "Total explored area: a", where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point. 
Output a blank line after each test case.

Sample Input

2
10 10 20 20
15 15 25 25.5
0

Sample Output

Test case #1
Total explored area: 180.00 

Source

Mid-Central European Regional Contest 2000

题解：

 题目的意思是给定n个矩形的2n个坐标，求矩形的覆盖面积。如果开一个大的bool数组，将覆盖过的部分更新为true，再从头到尾扫描一遍，在坐标范围比较小的情况下，可以求解。但是如果坐标x,y的取值范围很大，比如[-10^8,10^8]，用上面这个方法就不能求解了；而且坐标还有可能是实数，上面的方法就更加不可行了，需要寻找一种新的解法，就是下面要说到的“离散化”。
    注意到要表示一个矩形，只需要知道其2个顶点的坐标就可以了(最左下，最右上)。可以用2个数组x[0...2n-1]，y[0...2n-1]记录下矩形Ri的2个坐标(x1,y1)，(x2,y2)，然后将数组x[0...xn-1]，y[0...2n-1]排序，为下一步的扫描线作准备，这就是离散化的思想。这题还可以用线段树做进一步优化，但是这里只介绍离散化的思想。
    看下面这个例子：有2个矩形(1,1)，(3,3)和(2,2)，(4,4)。如图：

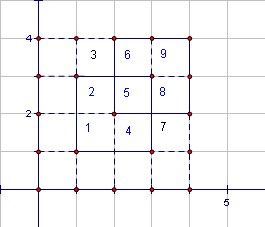
图中虚线表示扫描线，下一步工作只需要将这2个矩形覆盖过的部分的bool数组的对应位置更新为true，接下去用扫描线从左到右，从上到下扫描一遍，就可以求出矩形覆盖的总面积。
    这个图对应的bool数组的值如下：
    1 1 0                       1 2 3
    1 1 1       <---->       4 5 6
    0 1 1                       7 8 9

AC代码：

注意：：：：POJ1151上G++要用%.2f才能过！%.2lf WA！

#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=;
const double eps=1e-;
double ans=,x[N<<],y[N<<],pos[N][];
bool hash[N<<][N<<];
int cmp(const void *a,const void *b){
    double *aa=(double *)a;
    double *bb=(double *)b;
    if(fabs(*aa-*bb)<=eps) return ;
    else if(*aa-*bb>) return ;
    return -;
}
int main(){int i,j,k,n,x1,y1,x2,y2,cas=;
    while(scanf("%d",&n)==){
        if(!n) break;
        for(ans=k=i=;i<n;i++,k+=){
            scanf("%lf%lf%lf%lf",&pos[i][],&pos[i][],&pos[i][],&pos[i][]);
            x[k]=pos[i][];y[k]=pos[i][];x[k+]=pos[i][];y[k+]=pos[i][];
        }
        memset(hash,,sizeof hash);
        qsort(x,n<<,sizeof x[],cmp);
        qsort(y,n<<,sizeof y[],cmp);
        for(i=;i<n;i++){
            for(k=;fabs(x[k]-pos[i][])>eps;k++); x1=k;
            for(k=;fabs(y[k]-pos[i][])>eps;k++); y1=k;
            for(k=;fabs(x[k]-pos[i][])>eps;k++); x2=k;
            for(k=;fabs(y[k]-pos[i][])>eps;k++); y2=k;
            for(j=x1;j<x2;j++){
                for(k=y1;k<y2;k++){
                    hash[j][k]=;
                }
            }
        }
        for(i=;i<*n-;i++){
            for(j=;j<*n-;j++){
                ans+=hash[i][j]*(x[i+]-x[i])*(y[j+]-y[j]);
            }
        }
        printf("Test case #%d\n",++cas);
        printf("Total explored area: %.2lf\n\n",ans);
    }
    return ;
}