Codeforces554E:Love Triangles

There are many anime that are about "love triangles": Alice loves Bob, and Charlie loves Bob as well, but Alice hates Charlie. You are thinking about an anime which has n characters.
The characters are labeled from 1 to n.
Every pair of two characters can either mutually love each other or mutually hate each other (there is no neutral state).

You hate love triangles (A-B are in love and B-C are in love, but A-C hate each other), and you also hate it when nobody is in love. So, considering any three characters, you will be happy if exactly one pair is in love (A and B love each other, and C hates
both A and B), or if all three pairs are in love (A loves B, B loves C, C loves A).

You are given a list of m known relationships in the anime. You know for sure that certain pairs love each other, and certain pairs hate
each other. You're wondering how many ways you can fill in the remaining relationships so you are happy with every triangle. Two ways are considered different if two characters are in love in one way but hate each other in the other. Print this count modulo 1 000 000 007.

Input

The first line of input will contain two integers n, m (3 ≤ n ≤ 100 000, 0 ≤ m ≤ 100 000).

The next m lines will contain the description of the known relationships. The i-th
line will contain three integers ai, bi, ci.
If ci is
1, then aiand bi are
in love, otherwise, they hate each other (1 ≤ ai, bi ≤ n, ai ≠ bi, ).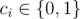

Each pair of people will be described no more than once.

Output

Print a single integer equal to the number of ways to fill in the remaining pairs so that you are happy with every triangle modulo1 000 000 007.

Sample test(s)

input

3 0

output

4

input

4 4
1 2 1
2 3 1
3 4 0
4 1 0

output

1

input

4 4
1 2 1
2 3 1
3 4 0
4 1 1

output

0

Note

In the first sample, the four ways are to:

• Make everyone love each other
• Make 1 and 2 love each other, and 3 hate 1 and 2 (symmetrically, we get 3 ways from this).

In the second sample, the only possible solution is to make 1 and 3 love each other and 2 and 4 hate each other.

题意：

给出一个无向图，要求加入几天边使得其成为一个全然图，使得随意三个点组成的环没有三角恋，或者互不相爱

思路：

而全然图是有条件的，首先我们给每条边按题目要求赋值，1代表相爱，0代表不相爱

那么对于随意三个点的三条边而言，必定仅仅有两种情况：所有为1。或者两个为0，一个为1

那么在按题目要求的输入先把确定的边构造好后。对于那些还没有构造的边我们能够分情况

1.假设有两条边是同色，那么还有一条边必须是1

2.假设两条边不同色，那么另外一条边必定是0

那么我们就能够用搜索完毕

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <bitset>
#include <list>
#include <algorithm>
#include <climits>
using namespace std;

#define lson 2*i
#define rson 2*i+1
#define LS l,mid,lson
#define RS mid+1,r,rson
#define UP(i,x,y) for(i=x;i<=y;i++)
#define DOWN(i,x,y) for(i=x;i>=y;i--)
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define LL long long
#define N 100005
#define INF 0x3f3f3f3f
#define EXP 1e-8
#define mpa make_pair
#define lowbit(x) (x&-x)
const int mod = 1e9+7;

vector<pair<int,int> > mat[N];
int n,m;
int vis[N];
LL ans;

void dfs(int u)
{
    for(int i = 0;i<mat[u].size();i++)
    {
        int v = mat[u][i].first;
        int p = mat[u][i].second;
        if(vis[v]==-1)
        {
            if(p==1)
            vis[v]=vis[u];
            else
            vis[v]=!vis[u];
            dfs(v);
        }
        if(p==1 && vis[u]!=vis[v])
        ans=0;
        if(p==0 && vis[u]==vis[v])
        ans=0;
    }
}

int main()
{
    int i,j,k,x,y,z;
    scanf("%d%d",&n,&m);
    while(m--)
    {
        scanf("%d%d%d",&x,&y,&z);
        mat[x].push_back(mpa(y,z));
        mat[y].push_back(mpa(x,z));
    }
    MEM(vis,-1);
    ans = (mod+1)/2;
    for(i = 1;i<=n;i++)
    {
        if(vis[i]==-1)
        {
            ans = (ans*2)%mod;
            vis[i] = 0;
            dfs(i);
        }
    }
    printf("%I64d\n",ans);

    return 0;
}