bzoj 5055: 膜法师 树状数组+离散

先枚举每一个数,看它前面有几个比它小,算一下和为sum1,后面有几个比它大,算一下和为sum2,对答案的贡献为A[i]*sum1*sum2。
离散化后,树状数组就可以了。
就是倒着一边,顺着一边,统计就ok了,离散是为了大小,先后顺序(方便去重)
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
#include<map>
#define mod 19260817
#define N 300007
#define ll long long
using namespace std; int n,top;
ll ans;
ll a[N],tree[N],c[N];
map<int,int>p;
struct Node
{
int zhi,id;
}b[N]; bool cmp(Node x,Node y)
{
return x.zhi<y.zhi;
}
int lowbit(int x){return x&(-x);}
ll query(int x)
{
ll res=;
for (int i=x;i>=;i-=lowbit(i))
res+=tree[i];
res%=mod;
return res;
}
void add(int x,ll z)
{
for (int i=x;i<=top;i+=lowbit(i))
tree[i]=(tree[i]+z)%mod;
}
int main()
{
p.clear();
scanf("%d",&n);
for (int i=;i<=n;i++)
{
scanf("%d",&a[i]);
a[i]%=mod;
b[i].zhi=a[i];
b[i].id=i;
}
sort(b+,b+n+,cmp);
b[].zhi=-;
for (int i=;i<=n;i++)
if (b[i].zhi!=b[i-].zhi) p[b[i].zhi]=++top;
for (int i=;i<=n;i++)
{
c[i]=1ll*query(p[a[i]]-)*a[i]%mod;
add(p[a[i]],a[i]);
}
memset(tree,,sizeof(tree));
for (int i=n;i>=;i--)
{
ans=(ans+1ll*c[i]*(query(top)-query(p[a[i]])+mod))%mod;
add(p[a[i]],a[i]);
}
printf("%lld",ans);
}
bzoj 5055: 膜法师 树状数组+离散的更多相关文章
- bzoj 5055: 膜法师 -- 树状数组
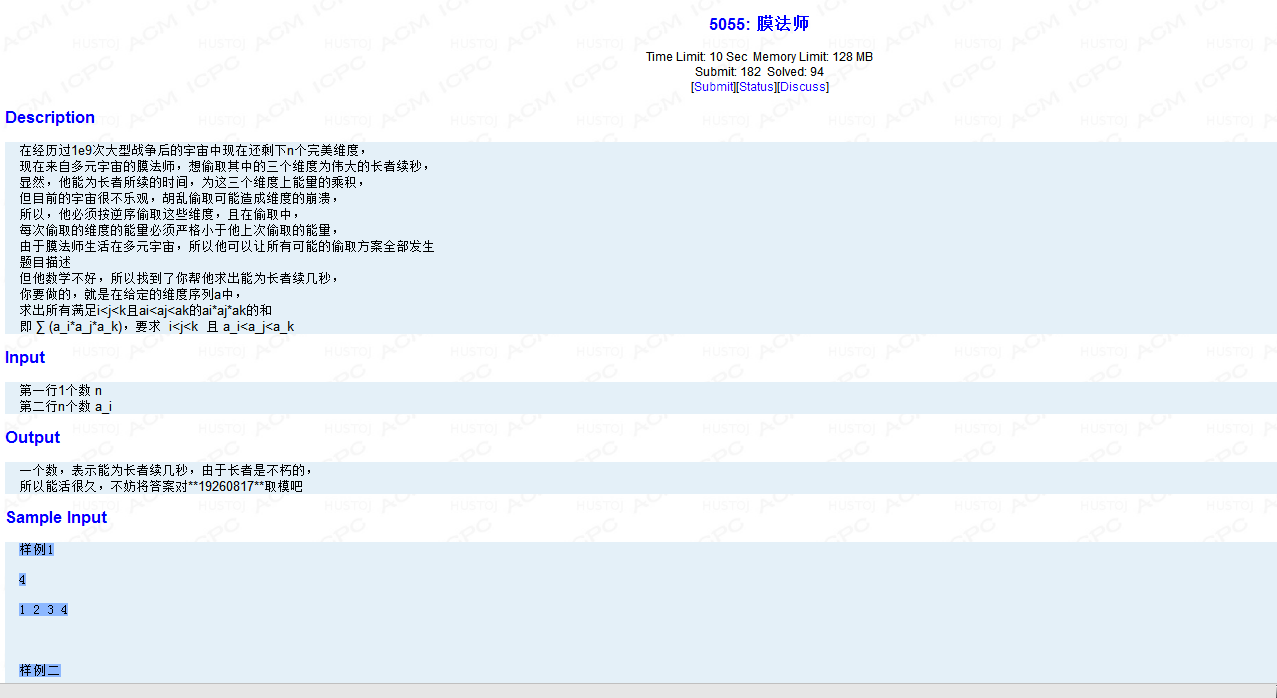
5055: 膜法师 Time Limit: 10 Sec Memory Limit: 128 MB Description 在经历过1e9次大型战争后的宇宙中现在还剩下n个完美维度, 现在来自多元宇 ...
- bzoj 5055: 膜法师——树状数组
Description 在经历过1e9次大型战争后的宇宙中现在还剩下n个完美维度, 现在来自多元宇宙的膜法师,想偷取其中的三个维度为伟大的长者续秒, 显然,他能为长者所续的时间,为这三个维度上能量的乘 ...
- 【BZOJ5055】膜法师 树状数组
[BZOJ5055]膜法师 Description 题目描述 在给定的维度序列a中, 求出所有满足i<j<k且ai<aj<ak的ai*aj*ak的和 即 ∑ (a_i*a_j* ...
- 【BZOJ】1818: [Cqoi2010]内部白点(树状数组+离散+特殊的技巧)
http://www.lydsy.com/JudgeOnline/problem.php?id=1818 这一题一开始我就看错了,bzoj的那个绝对值109简直坑人,应该是10^9,我直接写了个暴力. ...
- [BZOJ 5055]膜法师
Description 在经历过1e9次大型战争后的宇宙中现在还剩下n个完美维度, 现在来自多元宇宙的膜法师,想偷取其中的三个维度为伟大的长者续秒, 显然,他能为长者所续的时间,为这三个维度上能量的乘 ...
- Bzoj 2789: [Poi2012]Letters 树状数组,逆序对
2789: [Poi2012]Letters Time Limit: 20 Sec Memory Limit: 128 MBSubmit: 278 Solved: 185[Submit][Stat ...
- BZOJ 4361 isn | DP 树状数组
链接 BZOJ 4361 题面 给出一个长度为n的序列A(A1,A2...AN).如果序列A不是非降的,你必须从中删去一个数, 这一操作,直到A非降为止.求有多少种不同的操作方案,答案模10^9+7. ...
- BZOJ.1901.Dynamic Rankings(树状数组套主席树(动态主席树))
题目链接 BZOJ 洛谷 区间第k小,我们可以想到主席树.然而这是静态的,怎么支持修改? 静态的主席树是利用前缀和+差分来求解的,那么对于每个位置上的每棵树看做一个点,拿树状数组更新. 还是树状数组的 ...
- BZOJ 2727 双十字(树状数组)
题目链接:http://61.187.179.132/JudgeOnline/problem.php?id=2727 题意: 思路:思路来自这里.首先对于每个位置(i,j)用C[i][j]表示该位置同 ...
随机推荐
- nmon安装和使用介绍
使用参考地址:百度中搜索 nmon 博客园 使用文档参考地址:http://nmon.sourceforge.net/pmwiki.php?n=Site.Documentation nmmon地址:h ...
- 【iOS】UITableview cell 顶部空白的n种设置方法
我知道没人会主动设置这个东西,但是大家一定都遇到过这个问题,下面总结下可能是哪些情况: 1, self.automaticallyAdjustsScrollViewInsets = NO; 这个应该 ...
- 如何用JavaScript判断前端应用运行环境(移动平台还是桌面环境)
我们部署在某些云平台或者Web服务器上的前端应用,既可以用PC端浏览器访问,也可以用手机上的浏览器访问. 在前端应用里,有时候我们需要根据运行环境的不同做出对应处理.比如下面这段逻辑,如果判断出应用当 ...
- Scala 的list
9.1 使用列表 列表类型:跟数组一样,列表也是同质化的(homogeneous).即所有元素都要是同种类型. 列表结构:所有列表由两部分组成:Nil 和 ::(cons). 基本操作:主要有三个:h ...
- CentOS7——防火墙设置
1.查看firewall服务状态 systemctl status firewalld 2.查看firewall的状态firewall-cmd --state 3.开启.重启.关闭.firewalld ...
- valgrind测试程序内存泄漏问题
1.用wincap将valgrind放入系统任意路径下,解压 2. 登录主机后台在需要测试程序的路径下运行此行命令: /opt/valgrind/bin/valgrind ./itb(例) 3. 跑 ...
- What is the difference between try/except and assert?
assert only check if a condition is true or not and throw an exception. A try/except block can run a ...
- Spring框架针对dao层的jdbcTemplate操作crud之delete删除数据库操作 Spring相关Jar包下载
首先,找齐Spring框架中IoC功能.aop功能.JdbcTemplate功能所需的jar包,当前13个Jar包 1.Spring压缩包中的四个核心JAR包,实现IoC控制反转的根据xml配置文件或 ...
- Python学习笔记2(序列)
元组不可变序列 tuple函数 总结 字符串 基本字符串的操作 字符串格式化 字符串方法 find join lower replace split strip translate 小结 元组:不可变 ...
- 【线段树】bzoj3585: mex
非常精妙的线段树题 Description 有一个长度为n的数组{a1,a2,...,an}.m次询问,每次询问一个区间内最小没有出现过的自然数. Input 第一行n,m. 第二行为n个数. 从第三 ...
