ML一些零散记录

• 朴素贝叶斯的假定条件：变量独立同分布
• 一般情况下，越复杂的系统，过拟合的可能性就越高，一般模型相对简单的话泛化能力会更好一点，增加隐层数可以降低网络误差（也有文献认为不一定能有效降低），提高精度，但也使网络复杂化，从而增加了网络的训练时间和出现“过拟合”的倾向， svm高斯核函数比线性核函数模型更复杂，容易过拟合
• AdaBoost算法中不同的训练集是通过调整每个样本对应的权重来实现的。开始时，每个样本对应的权重是相同的，即其中n为样本个数，在此样本分布下训练出一弱分类器。对于分类错误的样本，加大其对应的权重；而对于分类正确的样本，降低其权重，这样分错的样本就被凸显出来，从而得到一个新的样本分布。在新的样本分布下，再次对样本进行训练，得到弱分类器。以此类推，将所有的弱分类器重叠加起来，得到强分类器。

• Bagging与Boosting的区别主要是取样方式不同:Bagging采用均匀取样，而Boosting根据错误率取样。Bagging的各个预测函数没有权重，而Boosting是有权重的。Bagging的各个预测函数可以并行生成，而Boosing的各个预测函数只能顺序生成。

• 神经网络学习过程的本质就是学习数据分布，在训练数据与测试数据分布不同情况下，模型的泛化能力就大大降低；另一方面，若训练过程中每批batch的数据分布也各不相同，那么网络每批迭代学习过程也会出现较大波动，使之更难趋于收敛，降低训练收敛速度。通常在输入层做标准化/归一化并不能保证每次minibatch通过每个层的输入数据都是均值0方差1，因此我们可以加一个batch normalization层对这个minibatch的数据进行处理。但是这样也带来一个问题，把某个层的输出限制在均值为0方差为1的分布会使得网络的表达能力变弱。因此又给batch normalization层进行一些限制的放松，给它增加两个可学习的参数 β 和 γ ，对数据进行缩放和平移，平移参数 β 和缩放参数 γ 是学习出来的。极端的情况这两个参数等于mini-batch的均值和方差，那么经过batch normalization之后的数据和输入完全一样，当然一般的情况是不同的。Batch normalization输出计算的统计量会受到batch中其他样本的影响（对一个batch里所有的图片的所有像素求均值和标准差。而instance norm是对单个图片的所有像素求均值和标准差）由于shuffle的存在，每个batch里每次的均值和标准差是不稳定，本身相当于是引入了噪声。而instance norm的信息都是来自于自身的图片，某个角度来说，可以看作是全局信息的一次整合和调整。对于训练也说也是更稳定的一种方法。在RNN里面（看hinton的layer normalization想到的）， 超分辨率或者对图像对比度、亮度等有要求的时候不建议使用BN。

  

• 生成模型是通过联合概率分布来求条件概率分布，而判别模型是通过数据直接求出条件概率分布，换句话说也就是，生成模型学习了所有数据的特点（更宽泛，更普适），判别模型则只是找出分界（更狭隘 更特殊）。

　　判别模型求解的思路是：条件分布------>模型参数后验概率最大------->（似然函数参数先验）最大------->最大似然

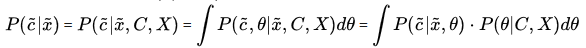　　即为求条件分布的参数关于训练数据（C,X）的后验分布

　　生成模型的求解思路是：联合分布------->求解类别先验概率和类别条件概率

　　

　　　常见的判别式模型有：

1. Logistic regression（logistical 回归）
2. Linear discriminant analysis（线性判别分析）
3. Supportvector machines（支持向量机）
4. Boosting（集成学习）
5. Conditional random fields（条件随机场）
6. Linear regression（线性回归）
7. Neural networks（神经网络）

常见的生成式模型有:

1. Gaussian mixture model and othertypes of mixture model（高斯混合及其他类型混合模型）
2. Hidden Markov model（隐马尔可夫）
3. NaiveBayes（朴素贝叶斯）
4. AODE（平均单依赖估计）
5. Latent Dirichlet allocation（LDA主题模型）
6. Restricted Boltzmann Machine（限制波兹曼机）

• 联合概率公式：$p(x,y) = p(x|y)p(y) = p(y|x)p(x)$，若x,y独立，则公式退化为$p(x,y) = p(x)p(y)$
• 从联合概率公式可以推导出条件概率公式：$p(x|y) = p(x,y)/p(y)$  $p(y|x) = p(x,y)/p(x)$
• 全概率公式：$p(x)=\sum_{m=1}^Mp(x|y_m)p(y_m)$，其中$\sum_{m=1}^Mp(y_m)=1$
• 贝叶斯（后验概率）公式：$p(y_m|x) = p(y_m,x)/p(x) = p(x|y_m)p(y_m)/\sum_{m=1}^Mp(x|y_m)p(y_m)$

　　$p(y_m|x)$：后验概率

　　    $p(x|y_m)$：先验概率

　　　 $p(y_m)$：似然函数

$sum_{m=1}^Mp(x|y_m)p(y_m) = p(x)$：证据因子