SDOJ 2605 闲荡

描述

L 饭后无聊，便在 BugTown 里闲荡。

BugTown 共有 N 栋房屋和 M 条有向道路。每栋房屋都有一个非负整数 vi 作为标识。

BugTown 有一个特性十分神奇：从任意一个房屋离开后沿着路走再也不会回到原地。

L 想选一个房屋作为闲荡的起点，之后，他会随机选择一条当前位置能走的道路顺其 走过去，如此反复直到没有能走的道路。

由于极度无聊， L 发明了一个游戏以为消遣。他在闲荡的过程中记录已经过的房屋标 识的异或和（含起点）。闲荡完后，他会得到一个数。

L希望对每个房屋算出以它为起点能得到的数的期望值，但是他不知道怎么算，只好 求助于你。

输入

第一行两个正整数 N; M 分别为房屋数和道路数。

第二行 N 个数为 vi。

接下来 M 行每行两个整数 ai; bi 描述一条 ai 到 bi 的道路

输出

输出共 N 行。第 i 行一个实数表示以 i 号房屋为起点时最后得到的数的期望值。 实数四舍五入到小数点后三位

样例输入

3 2
1 2 3
1 2
2 3

样例输出

0.000
1.000
3.000

对于 10% 的数据， N <= 5; M <= 10。

对于 30% 的数据， N, M<= 50。

对于 70% 的数据， N, M <=1000。

对于 100% 的数据， 1 <= N,M <= 1e5; 0 <= vi <= 1e9。

----------------------------------------------------------------------------------------------

数学期望真是一个大坑！异或的相关计算也是！趁这道题复习了一下这两点。

数学期望：是试验中每次可能结果的概率乘以其结果的总和

·这是公式：

·它有两个结论：

1.E(A + B) = E(A) + E(B)

2.E(k*A) = k*E(A)

看起来没什么用，但实际上太了不起啦（23333

好的然后我们来看这道题。

先从期望入手：

设某个点的标识为k，因为题目涉及到异或，所以有

k的二进制表示：

则：

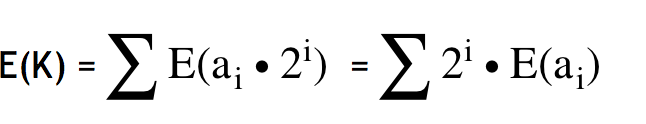
于是就转化为求E(ai)

而这时候，玄（投机）学（取巧）操作就出现了：因为ai只能为0或1，所以我们可以通过等式拆开化简来消去系数为0的项：

从此，我们将求E(ai)转化为直接求ai=1的概率，即只需要处理每个点出发得到的第i位为1的概率。

接下来我们要构造的是dp转移方程：

用f[c][d]表示从c点出发，此数位为d的概率。

枚举当前到的点u，此时数位为g，v为u的某出边，double p=1.0/出边数，以下分为两种情况：

1. u 没有出边，则有：f[u][g]=1; f[u][g^1]=0;//为g（0，1）的概率为1，为g相反的数（1，0）的概率为0

2. u有出边，则有递推式： f[u][0]+=f[v][g]*p; f[u][1]+=f[v][g^1]*p; //儿子当位为g，异或后为0，反之亦然

最后看回大局，最初应该先做一次拓扑排序，因为我们是以图的一层一层向下转移的。

就酱～

 #include<bits/stdc++.h>
 #define N 100010
 using namespace std;
 int val[N],n,m;
 struct rockdu
 {
     int u,v,nxt;
 }e[N*];
 int first[N],cnt;
 int tot;
 void ade(int u,int v)
 {
     e[++cnt].nxt=first[u];first[u]=cnt;
     e[cnt].v=v;e[cnt].u=u;
 }
 int deg[N],seq[N],sn;
 double f[N][];
 double ans[N];
 queue<int> q;
 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
         scanf("%d",&val[i]);
     for(int i=;i<=m;i++)
     {
         int a,b;
         scanf("%d%d",&a,&b);
         ade(a,b);
         ++deg[b];
     }
     for(int i=;i<=n;i++)
         if(deg[i]==) q.push(i);
     while(!q.empty())
     {
         int u=q.front(); q.pop();
         seq[++sn]=u;
         for(int i=first[u];i;i=e[i].nxt)
         {
             int v=e[i].v;
             deg[v]--;
             if(deg[v]==) q.push(v);
         }
     }
     for(int i=;i<;i++)
         for(int j=n;j>=;j--)
         {
             int u=seq[j],son=;
             int g=( (val[u]>>i)& );
             for(int x=first[u];x;x=e[x].nxt)
                 ++son;//记录儿子个数
             if(son==)
             {
                 f[u][g]=1.0;
                 f[u][g^]=0.0;
             }
             else
             {
                 double p=1.0/son;
                 f[u][]=f[u][]=0.0;//初始化
                 for(int x=first[u];x;x=e[x].nxt)
                 {
                     int v=e[x].v;
                     f[u][]+=f[v][g]*p;
                     f[u][]+=f[v][g^]*p;
                 }
             }
             ans[u]+=f[u][]*(<<i);
         }
     for(int i=;i<=n;i++)
         printf("%.3lf\n",ans[i]);
     return ;
 }

要看吗ovo