Codeforces Round #505 D. Recovering BST（区间DP）

首先膜一发网上的题解。大佬们tql。

给你n个单调递增的数字，问是否能够把这些数字重新构成一棵二叉搜索树（BST），且所有的父亲结点和叶子结点之间的gcd > 1？

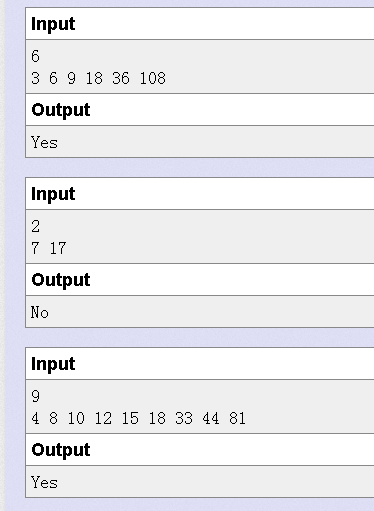
这个题场上是想暴力试试的。结果不行。发现符合最优子结构，可以DP。但是想不出来怎么转移。

看了大佬的题解。

若以第 k 个结点为根节点，用 L[i][k] 表示是否能够向左延伸到 i 点，R[k][j] 表示是否能够向右延伸到 j 点。

那么区间 [l, r] 合法，仅当 L[l][k] && R[k][r] == 1。

这样有了断点 k 作为[l, r]的根，就可以判断gcd能否用L[l][r] 和 R[l][r] 更新 R[l-1][r] 和 L[l][r+1]。

判断gcd可以预处理。

这样总复杂度是n^2 * logn

#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iostream>
using namespace std;
typedef long long LL;
const int maxn =  + ;

int n;
int a[maxn];
int v[maxn][maxn], L[maxn][maxn], R[maxn][maxn], C[maxn][maxn];
int dp[maxn][maxn][];

int main()
{
    scanf("%d", &n);
    for (int i = ; i <= n; i++)
    {
        L[i][i] = R[i][i] = ;
        scanf("%d", &a[i]);
    }

    for (int i = ; i <= n; i++)
    for (int j = i+; j <= n; j++)
        v[i][j] = v[j][i] = __gcd(a[i], a[j]) != ;

    int r;
    for (int len = ; len <= n; len++)
    for (int l = ; (r = l+len-) <= n; l++)
    for (int k = l; k <= r; k++)
        if (L[l][k] && R[k][r])
        {
            C[l][r] = ;
            if (v[k][l-]) R[l-][r] = ;
            if (v[k][r+]) L[l][r+] = ;
        }

    printf("%s\n", C[][n]?"Yes" : "No");
}