FSMC原理通俗解释

所以不用GPIO口直接驱动液晶，是因为这种方法速度太慢，而FSMC是用来外接各种存储芯片的，所以其数据通信速度是比普通GPIO口要快得多的。TFT-LCD 驱动芯片的读写时序和SRAM的差不多，所以就可以用FSMC四块中的SRAM块来驱动LCD。SRAM有数据线和地址线，所以FSMC跟它匹配同样也有数据线和地址线，而LCD数据线跟地址线共用，通信时用RS端来区分线上是数据还是指令，RS高是数据，RS低是指令。

其实这中间一开始最不理解就是与LCD的RS引脚相关的东西，那时候也不知道咋回事一直以为FSMC的地址线和数据线是共用的，导致我一直没明白怎么回事，昨天一看正点原子的探索者原理图才发现FSMC有数据线还有地址线，是分开的。驱动液晶的时候，数据线接液晶的并口，RS接到了FSMC的某个地址引脚。具体为什么这样接，也是我想着重记录的。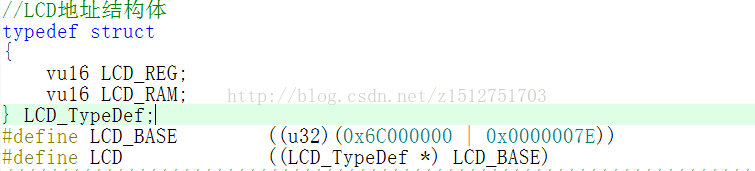

首先，FSMC是什么，FSMC我自己的理解就是，一个衔接CPU与外部存储的桥梁，它的功能呢就是你往相应的地址里写数据时候，你不需用软件来模拟外部存储芯片的读写时序，而只需配置好FSMC相关的时序寄存器，配置好相关寄存器之后，你只管往相应存储块中的地址里写数据就可以了。最直观的解释就看上边正点原子的一小段代码，代码中定义了一个结构体，然后强制性的把结构体的起始地址设在了0x6C000000 | 0x0000007E处。那么这个0x6C000000 | 0x0000007E地址是啥意思呢，其中0x6C000000是FSMC存储块1的区4起始地址，0x6C00007E为存储块1区4内的某个地址，你给LCD_REG赋值，就是往外部存储设备中的0x6C00007E地址处写数据，给LCD_RAM赋值，就是往0x6C00007F地址处写数据。这里是结构体，当然也可以是一个巨大的数组或其他数据类型。当然了，FSMC只是一个数据衔接部件，真正的存储芯片是需要通过引脚连接在FSMC的地址和数据引脚上的。存储芯片在指定地址写入数据的时候需要地址线来指定要写数据往哪个地址。也就是说上例中，往0x6C00007E中写数据的时候，地址线的低8位（0x7E）就是0111 1110。这就是FSMC的工作机制。

说完FSMC，下面说如何用FSMC的某跟地址线控制LCD的RS端。以RS连接到A6为例，TFT-LCD的数据是16位的，即读写一次数据为两个字节按字节编址的话就是所有的地址都是偶地址，LCD的显示RAM编址确实是按两个字节编址的。这样的话FSMC地址线上的0000 0001就代表AHB（FSMC是接到AHB总线上的）总线上的0000 0010,FSMC地址线上的0000 0010就代表AHB总线上的0000 0100，也就是说你在程序中写这个地址的时候总是要左移一位。造成这种现象的原因就是因为在配置FSMC传输数据位宽时设置成了16位。向LCD传输数据一次都是两个字节。所以对应上例，往地址0x6C00007E写数据，地址线的低8位并不是0111 1110，而是0011 1111。然后假如RS端连接在地址线A6端，那么也就是让A6端的高低来决定数据线上传输的是数据还是命令。上边说了，当往0x6C00007E地址（LCD_REG）写的时候，FSMC地址线低8位是0011 1111，A6（红色标出）为低电平，这时数据线上的是命令，所以写命令函数就是直接往LCD_REG写就行了，实际上就是为了让RS接低电平，当往0x6C00007F地址（LCD_RAM）中写时，FSMC地址线低8位是01000000，A6（红色标出）为高电平，这时数据线上是数据，所以写数据就直接往LCD_RAM中写，实际是为了让RS接高电平。

当然了，这里RS接的是A6，其他场合，RS可能接的是其他地址线，只需要根据上边的规律技巧来改变“0x6C000000 | 0x0000007E”中后者就可以了。这里这个RS的接法和用法很巧妙，摘自正点原子。

作者：z1512751703
来源：CSDN
原文：https://blog.csdn.net/z1512751703/article/details/78937117
版权声明：本文为博主原创文章，转载请附上博文链接！