POJ 3744 Scout YYF I：概率dp

题目链接：http://poj.org/problem?id=3744

题意：

　　有n个地雷，位置为pos[i]。

　　在每个位置，你向前走一步的概率为p，向前走两步的概率为1-p。

　　你的初始位置为1。

　　问你通过雷区的概率。

题解：

　　表示状态：

　　　　dp[i] = probability moving to i

　　　　表示走到i的概率

　　找出答案：

　　　　ans = dp[last_mine+1]

　　　　last_mine：最右边一颗雷的位置

　　如何转移：

　　　　dp[i] = dp[i-1] * p + dp[i-2] * (1-p)

　　　　if(i is a mine) dp[i] = 0

　　　　对于位置i，有可能是从i-1走来的，也有可能是从i-2走来的。

　　　　加法原理。

　　边界条件：

　　　　dp[1] = 1

　　　　初始位置为1。

　　优化：

　　　　矩阵快速幂。

　　　　对于某一段没有地雷的区间，是满足矩阵快速幂的（只用到递推式，dp不改为0）。

　　　　所以分段进行矩阵快速幂。

　　　　

　　　　将雷区划分为n段：

　　　　1~pos[1], pos[1]+1~pos[2], pos[2]+1~pos[3]...

　　　　

　　　　容斥原理：P（通过某一段雷区） = 1 - P（踩到最右边的雷）

　　　　乘法原理：P（通过总雷区） = ∏ P（通过每一段雷区）

　　　　矩阵格式：

　　　　

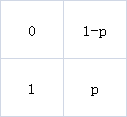
　　　　初始矩阵：

　　　　

　　　　特殊矩阵：

　　　　

AC Code:

 // state expression:
 // dp[i] = probability moving to i
 //
 // find the answer:
 // dp[last mine + 1]
 //
 // transferring:
 // dp[i] = dp[i-1] * p + dp[i-2] * (1-p)
 //
 // boundary:
 // dp[1] = 1
 // others = 0
 //
 // optimization:
 // quick pow for matrix
 // from x to y
 // res = start * special ^ (y-x)
 // dp[i] = res.val[0][0]
 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 #include <algorithm>
 #define MAX_N 15
 #define MAX_L 5

 using namespace std;

 struct Mat
 {
     int n;
     int m;
     double val[MAX_L][MAX_L];
     Mat()
     {
         n=;
         m=;
         memset(val,,sizeof(val));
     }
     void print_mat()
     {
         for(int i=;i<n;i++)
         {
             for(int j=;j<m;j++)
             {
                 cout<<val[i][j]<<" ";
             }
             cout<<endl;
         }
         cout<<endl;
     }
 };

 int n;
 int pos[MAX_N];
 double p;
 double ans;

 Mat make_unit(int k)
 {
     Mat mat;
     mat.n=k;
     mat.m=k;
     for(int i=;i<k;i++)
     {
         mat.val[i][i]=;
     }
     return mat;
 }

 Mat make_start()
 {
     Mat mat;
     mat.n=;
     mat.m=;
     mat.val[][]=;
     mat.val[][]=;
     return mat;
 }

 Mat make_special()
 {
     Mat mat;
     mat.n=;
     mat.m=;
     mat.val[][]=;
     mat.val[][]=-p;
     mat.val[][]=;
     mat.val[][]=p;
     return mat;
 }

 Mat mul_mat(const Mat &a,const Mat &b)
 {
     Mat c;
     if(a.m!=b.n)
     {
         cout<<"Error: mul_mat"<<endl;
         return c;
     }
     c.n=a.n;
     c.m=b.m;
     for(int i=;i<a.n;i++)
     {
         for(int j=;j<b.m;j++)
         {
             for(int k=;k<a.m;k++)
             {
                 c.val[i][j]+=a.val[i][k]*b.val[k][j];
             }
         }
     }
     return c;
 }

 Mat quick_pow_mat(Mat mat,long long k)
 {
     Mat ans;
     if(mat.n!=mat.m)
     {
         cout<<"Error: quick_pow_mat"<<endl;
         return ans;
     }
     ans=make_unit(mat.n);
     while(k)
     {
         if(k&)
         {
             ans=mul_mat(ans,mat);
         }
         mat=mul_mat(mat,mat);
         k>>=;
     }
     return ans;
 }

 void read()
 {
     pos[]=;
     for(int i=;i<=n;i++)
     {
         cin>>pos[i];
     }
 }

 void solve()
 {
     sort(pos+,pos++n);
     Mat special=make_special();
     ans=;
     for(int i=;i<=n;i++)
     {
         Mat start=make_start();
         Mat res=mul_mat(start,quick_pow_mat(special,pos[i]-pos[i-]));
         ans*=(-res.val[][]);
     }
 }

 void print()
 {
     printf("%.7f\n",ans);
 }

 int main()
 {
     while(cin>>n>>p)
     {
         read();
         solve();
         print();
     }
 }