kmeans算法原理以及实践操作(多种k值确定以及如何选取初始点方法)

kmeans一般在数据分析前期使用，选取适当的k，将数据聚类后，然后研究不同聚类下数据的特点。

算法原理：

(1) 随机选取k个中心点；

(2) 在第j次迭代中，对于每个样本点，选取最近的中心点，归为该类；

(3) 更新中心点为每类的均值；

(4) j<-j+1 ,重复(2)(3)迭代更新，直至误差小到某个值或者到达一定的迭代步数，误差不变.

空间复杂度o(N)

时间复杂度o(I*K*N)

其中N为样本点个数，K为中心点个数，I为迭代次数

为什么迭代后误差逐渐减小：

SSE= 

对于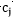 而言，求导后，当 时，SSE最小，对应第(3)步；

对于 而言，求导后，当 时，SSE最小，对应第(2)步。

因此kmeans迭代能使误差逐渐减少直到不变

轮廓系数：

轮廓系数（Silhouette Coefficient）结合了聚类的凝聚度（Cohesion）和分离度（Separation），用于评估聚类的效果。该值处于-1~1之间，值越大，表示聚类效果越好。具体计算方法如下：

1. 对于每个样本点i，计算点i与其同一个簇内的所有其他元素距离的平均值，记作a(i)，用于量化簇内的凝聚度。
2. 选取i外的一个簇b，计算i与b中所有点的平均距离，遍历所有其他簇，找到最近的这个平均距离,记作b(i)，即为i的邻居类，用于量化簇之间分离度。
3. 对于样本点i，轮廓系数s(i) = (b(i) – a(i))/max{a(i),b(i)}
4. 计算所有x的轮廓系数，求出平均值即为当前聚类的整体轮廓系数，度量数据聚类的紧密程度

从上面的公式，不难发现若s(i)小于0，说明i与其簇内元素的平均距离小于最近的其他簇，表示聚类效果不好。如果a(i)趋于0，或者b(i)足够大，即a(i)<<b(i)，那么s(i)趋近与1，说明聚类效果比较好。

K值确定

法1：(轮廓系数)在实际应用中，由于Kmean一般作为数据预处理，或者用于辅助分聚类贴标签。所以k一般不会设置很大。可以通过枚举，令k从2到一个固定值如10，在每个k值上重复运行数次kmeans(避免局部最优解)，并计算当前k的平均轮廓系数，最后选取轮廓系数最大的值对应的k作为最终的集群数目。

法2：(Calinski-Harabasz准则)

其中SSB是类间方差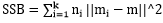， ，m为所有点的中心点,mi为某类的中心点；

SSW是类内方差，；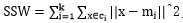

(N-k)/(k-1)是复杂度；

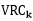比率越大，数据分离度越大.

前提：

Duda-Hart test 看数据集是否适合分为超过1类

初始点选择方法：

思想，初始的聚类中心之间相互距离尽可能远.

法1(kmeans++):

1、从输入的数据点集合中随机选择一个点作为第一个聚类中心

2、对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)

3、选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大

4、重复2和3直到k个聚类中心被选出来

5、利用这k个初始的聚类中心来运行标准的k-means算法

从上面的算法描述上可以看到，算法的关键是第3步，如何将D(x)反映到点被选择的概率上，一种算法如下：

1、先从我们的数据库随机挑个随机点当“种子点”

2、对于每个点，我们都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。

3、然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D(x))中的随机值Random，然后用Random -= D(x)，直到其<=0，此时的点就是下一个“种子点”。

4、重复2和3直到k个聚类中心被选出来

5、利用这k个初始的聚类中心来运行标准的k-means算法

法2：选用层次聚类或Canopy算法进行初始聚类，然后从k个类别中分别随机选取k个点

，来作为kmeans的初始聚类中心点

优点：

1、 算法快速、简单;

2、 容易解释

3、 聚类效果中上

4、 适用于高维

缺陷：

1、 对离群点敏感，对噪声点和孤立点很敏感(通过k-centers算法可以解决)

2、 K-means算法中聚类个数k的初始化

3、初始聚类中心的选择，不同的初始点选择可能导致完全不同的聚类结果。

实践操作：

R语言

1、####################判断是否应该分为超过1类##########################

dudahart2(x,clustering,alpha=0.001)

2、###################判断使用轮廓系数或Calinski-Harabasz准则选用k值，以及是否使用大规模样本点处理方式##########################################

pamk(data,krange=2:10,criterion="asw", usepam=TRUE,

scaling=FALSE, alpha=0.001, diss=inherits(data, "dist"),    critout=FALSE, ns=10, seed=NULL, ...)

3、############利用pamk求出来的k,用kmeans聚类####################

pamk.result <- pamk(data)

pamk.result$nc

kc <- kmeans(data, pamk.result$nc)

4、############画出k与轮廓系数关系，求出拐点值########################

# 0-1 正规化数据

min.max.norm <- function(x){

(x-min(x))/(max(x)-min(x))

}

raw.data <- iris[,1:4]

norm.data <- data.frame(sl = min.max.norm(raw.data[,1]),

sw = min.max.norm(raw.data[,2]),

pl = min.max.norm(raw.data[,3]),

pw = min.max.norm(raw.data[,4]))

## k取2到8，评估K

K <- 2:8

round <- 30 # 每次迭代30次，避免局部最优

rst <- sapply(K, function(i){

print(paste("K=",i))

mean(sapply(1:round,function(r){

print(paste("Round",r))

result <- kmeans(norm.data, i)

stats <- cluster.stats(dist(norm.data), result$cluster)

stats$avg.silwidth

}))

})

plot(K,rst,type='l',main='轮廓系数与K的关系', ylab='轮廓系数')

5、层次聚类得出k-means初始点

iris.hc <- hclust( dist(iris[,1:4]))

# plot( iris.hc, hang = -1)

plclust( iris.hc, labels = FALSE, hang = -1)

re <- rect.hclust(iris.hc, k = 3)

iris.id <- cutree(iris.hc, 3)######得出类别##########

6、################采用kmeans++选用k个初始点##################################

n<-length(x)

seed<-round(runif(1,1,n))

for ( i in 1:k){

if(i==1){ seed[i]<- round(runif(1,1,N)) }

dd<-0

tmp<-0

for(s in 1:n)

{

m<-length(seed)

for (j in 1:m) {

if(j==1){ tmp<-dist(x[s],seed[j]) }

else

{

tmptwo<-tmp

tmp<-dist(x[s],seed[j])

if(tmp>tmptwo)tmp<-tmptwo

}

}

dd[s]<-tmp

}

sumd<-sum(dd)

random<--round(runif(1,0, sumd))

for(ii in 1:n)

{

if(random<=0){break};

else{

random<-random-dd[ii]

}

}

seed[i+1]<-ii

}