浅谈算法和数据结构: 七 二叉查找树 八 平衡查找树之2-3树 九 平衡查找树之红黑树 十 平衡查找树之B树

http://www.cnblogs.com/yangecnu/p/Introduce-Binary-Search-Tree.html

前文介绍了符号表的两种实现，无序链表和有序数组，无序链表在插入的时候具有较高的灵活性，而有序数组在查找时具有较高的效率，本文介绍的二叉查找树(Binary Search Tree，BST)这一数据结构综合了以上两种数据结构的优点。

二叉查找树具有很高的灵活性，对其优化可以生成平衡二叉树，红黑树等高效的查找和插入数据结构，后文会一一介绍。

一 定义

二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree）,排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

3. 任意节点的左、右子树也分别为二叉查找树。

4. 没有键值相等的节点（no duplicate nodes）。

如下图，这个是普通的二叉树：

在此基础上，加上节点之间的大小关系，就是二叉查找树：

二 实现

在实现中，我们需要定义一个内部类Node，它包含两个分别指向左右节点的Node，一个用于排序的Key，以及该节点包含的值Value，还有一个记录该节点及所有子节点个数的值Number。

public class BinarySearchTreeSymbolTable<TKey, TValue> : SymbolTables<TKey, TValue> where TKey : IComparable<TKey>, IEquatable<TValue>
{
    private Node root;
    private class Node
    {
        public Node Left { get; set; }
        public Node Right { get; set; }
        public int Number { get; set; }
        public TKey Key { get; set; }
        public TValue Value { get; set; }

        public Node(TKey key, TValue value, int number)
        {
            this.Key = key;
            this.Value = value;
            this.Number = number;
        }
    }
...
}

查找

查找操作和二分查找类似，将key和节点的key比较，如果小于，那么就在Left Node节点查找,如果大于，则在Right Node节点查找，如果相等，直接返回Value。

该方法实现有迭代和递归两种。

递归的方式实现如下：

public override TValue Get(TKey key)
{
    TValue result = default(TValue);
    Node node = root;
    while (node != null)
    {

        if (key.CompareTo(node.Key) > 0)
        {
            node = node.Right;
        }
        else if (key.CompareTo(node.Key) < 0)
        {
            node = node.Left;
        }
        else
        {
            result = node.Value;
            break;
        }
    }
    return result;
}

迭代的如下：

public TValue Get(TKey key)
{
    return GetValue(root, key);
}

private TValue GetValue(Node root, TKey key)
{
    if (root == null) return default(TValue);
    int cmp = key.CompareTo(root.Key);
    if (cmp > 0) return GetValue(root.Right, key);
    else if (cmp < 0) return GetValue(root.Left, key);
    else return root.Value;
}

插入

插入和查找类似，首先查找有没有和key相同的，如果有，更新；如果没有找到，那么创建新的节点。并更新每个节点的Number值，代码实现如下：

public override void Put(TKey key, TValue value)
{
    root = Put(root, key, value);
}

private Node Put(Node x, TKey key, TValue value)
{
    //如果节点为空，则创建新的节点，并返回
    //否则比较根据大小判断是左节点还是右节点，然后继续查找左子树还是右子树
    //同时更新节点的Number的值
    if (x == null) return new Node(key, value, 1);
    int cmp = key.CompareTo(x.Key);
    if (cmp < 0) x.Left = Put(x.Left, key, value);
    else if (cmp > 0) x.Right = Put(x.Right, key, value);
    else x.Value = value;
    x.Number = Size(x.Left) + Size(x.Right) + 1;
    return x;
}

private int Size(Node node)
{
    if (node == null) return 0;
    else return node.Number;
}

插入操作图示如下：

下面是插入动画效果：

随机插入形成树的动画如下，可以看到，插入的时候树还是能够保持近似平衡状态：

最大最小值

如下图可以看出，二叉查找树的最大最小值是有规律的：

从图中可以看出，二叉查找树中，最左和最右节点即为最小值和最大值，所以我们只需迭代调用即可。

public override TKey GetMax()
{
    TKey maxItem = default(TKey);
    Node s = root;
    while (s.Right != null)
    {
        s = s.Right;
    }
    maxItem = s.Key;
    return maxItem;
}

public override TKey GetMin()
{
    TKey minItem = default(TKey);
    Node s = root;
    while (s.Left != null)
    {
        s = s.Left;
    }
    minItem = s.Key;
    return minItem;
}

以下是递归的版本：

public TKey GetMaxRecursive()
{
    return GetMaxRecursive(root);
}

private TKey GetMaxRecursive(Node root)
{
    if (root.Right == null) return root.Key;
    return GetMaxRecursive(root.Right);
}

public TKey GetMinRecursive()
{
    return GetMinRecursive(root);
}

private TKey GetMinRecursive(Node root)
{
    if (root.Left == null) return root.Key;
    return GetMinRecursive(root.Left);
}

Floor和Ceiling

查找Floor(key)的值就是所有<=key的最大值，相反查找Ceiling的值就是所有>=key的最小值，下图是Floor函数的查找示意图：

以查找Floor为例，我们首先将key和root元素比较，如果key比root的key小，则floor值一定在左子树上；如果比root的key大，则有可能在右子树上，当且仅当其右子树有一个节点的key值要小于等于该key；如果和root的key相等，则floor值就是key。根据以上分析，Floor方法的代码如下，Ceiling方法的代码类似，只需要把符号换一下即可：

public TKey Floor(TKey key)
{
    Node x = Floor(root, key);
    if (x != null) return x.Key;
    else return default(TKey);
}

private Node Floor(Node x, TKey key)
{
    if (x == null) return null;
    int cmp = key.CompareTo(x.Key);
    if (cmp == 0) return x;
    if (cmp < 0) return Floor(x.Left, key);
    else
    {
        Node right = Floor(x.Right, key);
        if (right == null) return x;
        else return right;
    }
}

删除

删除元素操作在二叉树的操作中应该是比较复杂的。首先来看下比较简单的删除最大最小值得方法。

以删除最小值为例，我们首先找到最小值，及最左边左子树为空的节点，然后返回其右子树作为新的左子树。操作示意图如下：

代码实现如下：

public void DelMin()
{
    root = DelMin(root);
}

private Node DelMin(Node root)
{
    if (root.Left == null) return root.Right;
    root.Left = DelMin(root.Left);
    root.Number = Size(root.Left) + Size(root.Right) + 1;
    return root;
}

删除最大值也是类似。

现在来分析一般情况，假定我们要删除指定key的某一个节点。这个问题的难点在于：删除最大最小值的操作，删除的节点只有1个子节点或者没有子节点，这样比较简单。但是如果删除任意节点，就有可能出现删除的节点有0个，1 个，2个子节点的情况，现在来逐一分析。

当删除的节点没有子节点时，直接将该父节点指向该节点的link设置为null。

当删除的节点只有1个子节点时，将该自己点替换为要删除的节点即可。

当删除的节点有2个子节点时，问题就变复杂了。

假设我们删除的节点t具有两个子节点。因为t具有右子节点，所以我们需要找到其右子节点中的最小节点，替换t节点的位置。这里有四个步骤：

1. 保存带删除的节点到临时变量t

2. 将t的右节点的最小节点min(t.right)保存到临时节点x

3. 将x的右节点设置为deleteMin(t.right)，该右节点是删除后，所有比x.key最大的节点。

4. 将x的做节点设置为t的左节点。

整个过程如下图：

对应代码如下：

public void Delete(TKey key)
{
    root =Delete(root, key);

}

private Node Delete(Node x, TKey key)
{
    int cmp = key.CompareTo(x.Key);
    if (cmp > 0) x.Right = Delete(x.Right, key);
    else if (cmp < 0) x.Left = Delete(x.Left, key);
    else
    {
        if (x.Left == null) return x.Right;
        else if (x.Right == null) return x.Left;
        else
        {
            Node t = x;
            x = GetMinNode(t.Right);
            x.Right = DelMin(t.Right);
            x.Left = t.Left;
        }
    }
    x.Number = Size(x.Left) + Size(x.Right) + 1;
    return x;
}

private Node GetMinNode(Node x)
{
    if (x.Left == null) return x;
    else return GetMinNode(x.Left);
}

以上二叉查找树的删除节点的算法不是完美的，因为随着删除的进行，二叉树会变得不太平衡，下面是动画演示。

三 分析

二叉查找树的运行时间和树的形状有关，树的形状又和插入元素的顺序有关。在最好的情况下，节点完全平衡，从根节点到最底层叶子节点只有lgN个节点。在最差的情况下，根节点到最底层叶子节点会有N各节点。在一般情况下，树的形状和最好的情况接近。

在分析二叉查找树的时候，我们通常会假设插入的元素顺序是随机的。对BST的分析类似与快速排序中的查找：

BST中位于顶部的元素就是快速排序中的第一个划分的元素，该元素左边的元素全部小于该元素，右边的元素均大于该元素。

对于N个不同元素，随机插入的二叉查找树来说，其平均查找/插入的时间复杂度大约为2lnN，这个和快速排序的分析一样，具体的证明方法不再赘述，参照快速排序。

四 总结

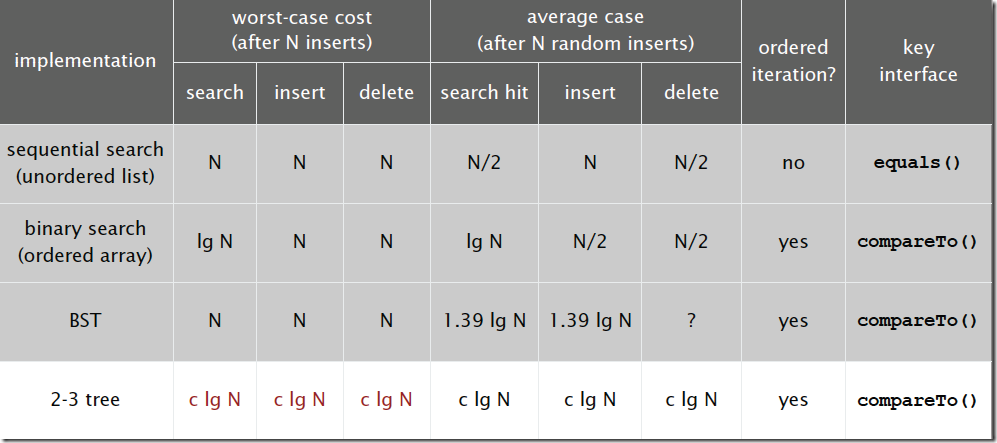
有了前篇文章 二分查找的分析，对二叉查找树的理解应该比较容易。下面是二叉查找树的时间复杂度：

它和二分查找一样，插入和查找的时间复杂度均为lgN，但是在最坏的情况下仍然会有N的时间复杂度。原因在于插入和删除元素的时候，树没有保持平衡。我们追求的是在最坏的情况下仍然有较好的时间复杂度，这就是后面要讲的平衡查找树的内容了。下文首先讲解平衡查找树的最简单的一种：2-3查找树。

希望本文对您了解二叉查找树有所帮助。

http://www.cnblogs.com/yangecnu/p/Introduce-2-3-Search-Tree.html

浅谈算法和数据结构: 八 平衡查找树之2-3树

 

前面介绍了二叉查找树(Binary Search Tree)，他对于大多数情况下的查找和插入在效率上来说是没有问题的，但是他在最差的情况下效率比较低。本文及后面文章介绍的平衡查找树的数据结构能够保证在最差的情况下也能达到lgN的效率，要实现这一目标我们需要保证树在插入完成之后始终保持平衡状态，这就是平衡查找树(Balanced Search Tree)。在一棵具有N 个节点的树中，我们希望该树的高度能够维持在lgN左右，这样我们就能保证只需要lgN次比较操作就可以查找到想要的值。不幸的是，每次插入元素之后维持树的平衡状态太昂贵。所以这里会介绍一些新的数据结构来保证在最坏的情况下插入和查找效率都能保证在对数的时间复杂度内完成。本文首先介绍2-3查找树(2-3 Search Tree)，后面会在此基础上介绍红黑树和B树。

定义

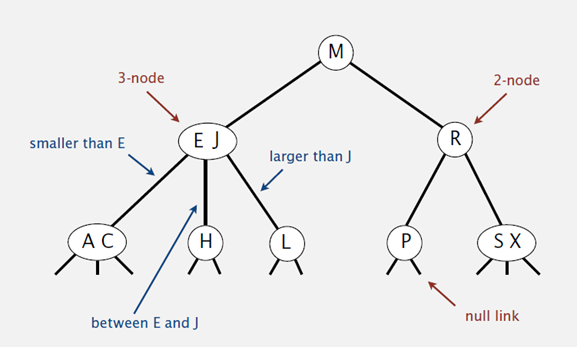
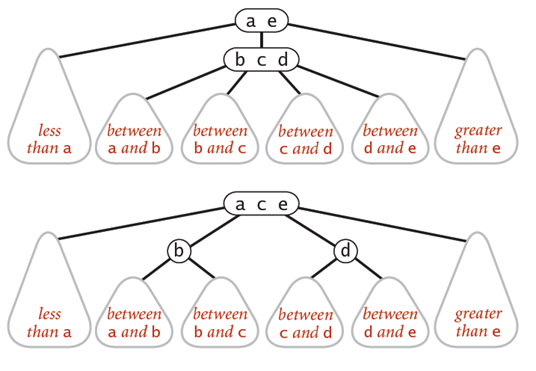
和二叉树不一样，2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node)，他保存1个key和左右两个自己点。对应3节点(3-node)，保存两个Key，2-3查找树的定义如下：

1. 要么为空，要么：

2. 对于2节点，该节点保存一个key及对应value，以及两个指向左右节点的节点，左节点也是一个2-3节点，所有的值都比key有效，有节点也是一个2-3节点，所有的值比key要大。

3. 对于3节点，该节点保存两个key及对应value，以及三个指向左中右的节点。左节点也是一个2-3节点，所有的值均比两个key中的最小的key还要小；中间节点也是一个2-3节点，中间节点的key值在两个跟节点key值之间；右节点也是一个2-3节点，节点的所有key值比两个key中的最大的key还要大。

如果中序遍历2-3查找树，就可以得到排好序的序列。在一个完全平衡的2-3查找树中，根节点到每一个为空节点的距离都相同。

查找

在进行2-3树的平衡之前，我们先假设已经处于平衡状态，我们先看基本的查找操作。

2-3树的查找和二叉查找树类似，要确定一个树是否属于2-3树，我们首先和其跟节点进行比较，如果相等，则查找成功；否则根据比较的条件，在其左中右子树中递归查找，如果找到的节点为空，则未找到，否则返回。查找过程如下图：

插入

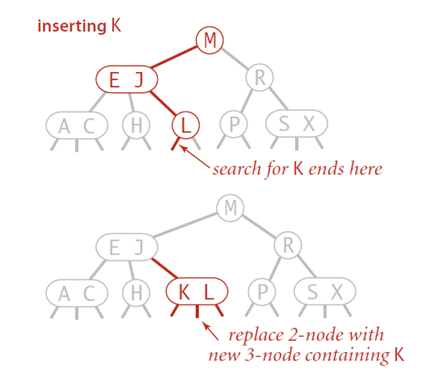
往一个2-node节点插入

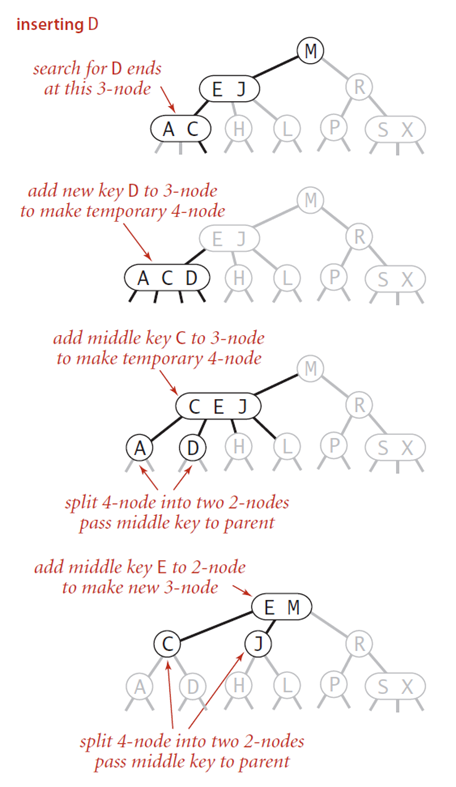
往2-3树中插入元素和往二叉查找树中插入元素一样，首先要进行查找，然后将节点挂到未找到的节点上。2-3树之所以能够保证在最差的情况下的效率的原因在于其插入之后仍然能够保持平衡状态。如果查找后未找到的节点是一个2-node节点，那么很容易，我们只需要将新的元素放到这个2-node节点里面使其变成一个3-node节点即可。但是如果查找的节点结束于一个3-node节点，那么可能有点麻烦。

往一个3-node节点插入

往一个3-node节点插入一个新的节点可能会遇到很多种不同的情况，下面首先从一个最简单的只包含一个3-node节点的树开始讨论。

只包含一个3-node节点

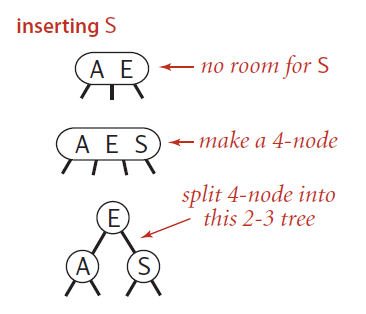
如上图，假设2-3树只包含一个3-node节点，这个节点有两个key，没有空间来插入第三个key了，最自然的方式是我们假设这个节点能存放三个元素，暂时使其变成一个4-node节点，同时他包含四个子节点。然后，我们将这个4-node节点的中间元素提升，左边的节点作为其左节点，右边的元素作为其右节点。插入完成，变为平衡2-3查找树，树的高度从0变为1。

节点是3-node，父节点是2-node

和第一种情况一样，我们也可以将新的元素插入到3-node节点中，使其成为一个临时的4-node节点，然后，将该节点中的中间元素提升到父节点即2-node节点中，使其父节点成为一个3-node节点，然后将左右节点分别挂在这个3-node节点的恰当位置。操作如下图：

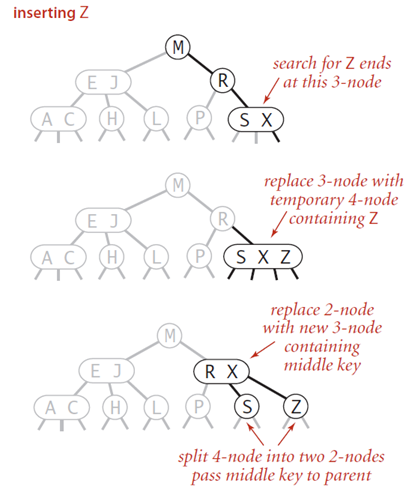
节点是3-node，父节点也是3-node

当我们插入的节点是3-node的时候，我们将该节点拆分，中间元素提升至父节点，但是此时父节点是一个3-node节点，插入之后，父节点变成了4-node节点，然后继续将中间元素提升至其父节点，直至遇到一个父节点是2-node节点，然后将其变为3-node，不需要继续进行拆分。

根节点分裂

当根节点到字节点都是3-node节点的时候，这是如果我们要在字节点插入新的元素的时候，会一直查分到跟节点，在最后一步的时候，跟节点变成了一个4-node节点，这个时候，就需要将跟节点查分为两个2-node节点，树的高度加1，这个操作过程如下：

本地转换

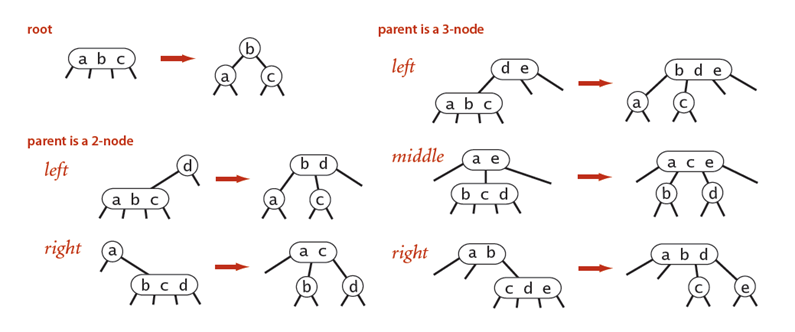
将一个4-node拆分为2-3node涉及到6种可能的操作。这4-node可能在跟节点，也可能是2-node的左子节点或者右子节点。或者是一个3-node的左，中，右子节点。所有的这些改变都是本地的，不需要检查或者修改其他部分的节点。所以只需要常数次操作即可完成2-3树的平衡。

性质

这些本地操作保持了2-3树的平衡。对于4-node节点变形为2-3节点，变形前后树的高度没有发生变化。只有当跟节点是4-node节点，变形后树的高度才加一。如下图所示：

分析

完全平衡的2-3查找树如下图，每个根节点到叶子节点的距离是相同的：

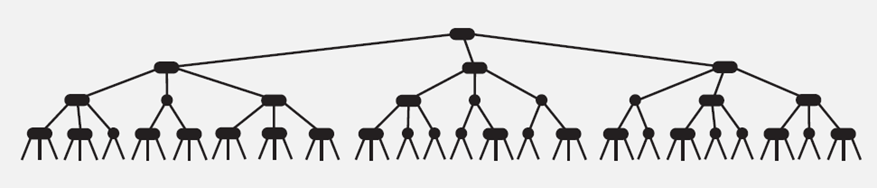
2-3树的查找效率与树的高度是息息相关的。

• 在最坏的情况下，也就是所有的节点都是2-node节点，查找效率为lgN
• 在最好的情况下，所有的节点都是3-node节点，查找效率为log₃N约等于0.631lgN

距离来说，对于1百万个节点的2-3树，树的高度为12-20之间，对于10亿个节点的2-3树，树的高度为18-30之间。

对于插入来说，只需要常数次操作即可完成，因为他只需要修改与该节点关联的节点即可，不需要检查其他节点，所以效率和查找类似。下面是2-3查找树的效率：

实现

直接实现2-3树比较复杂，因为：

1. 需要处理不同的节点类型，非常繁琐
2. 需要多次比较操作来将节点下移
3. 需要上移来拆分4-node节点
4. 拆分4-node节点的情况有很多种

2-3查找树实现起来比较复杂，在某些情况插入后的平衡操作可能会使得效率降低。在2-3查找树基础上改进的红黑树不仅具有较高的效率，并且实现起来较2-3查找树简单。

但是2-3查找树作为一种比较重要的概念和思路对于后文要讲到的红黑树和B树非常重要。希望本文对您了解2-3查找树有所帮助

http://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html

浅谈算法和数据结构: 九 平衡查找树之红黑树

 

前面一篇文章介绍了2-3查找树，可以看到，2-3查找树能保证在插入元素之后能保持树的平衡状态，最坏情况下即所有的子节点都是2-node，树的高度为lgN，从而保证了最坏情况下的时间复杂度。但是2-3树实现起来比较复杂，本文介绍一种简单实现2-3树的数据结构，即红黑树（Red-Black Tree）

定义

红黑树的主要是像是对2-3查找树进行编码，尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型，红色链接，他用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的，使用红色链接的两个2-nodes来表示一个3-nodes节点，并且向左倾斜，即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改，和普通的二叉查找树相同。

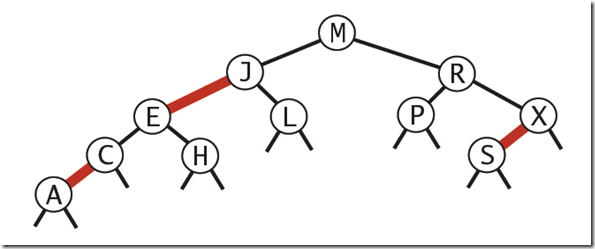
根据以上描述，红黑树定义如下：

红黑树是一种具有红色和黑色链接的平衡查找树，同时满足：

• 红色节点向左倾斜
• 一个节点不可能有两个红色链接
• 整个书完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同。

下图可以看到红黑树其实是2-3树的另外一种表现形式：如果我们将红色的连线水平绘制，那么他链接的两个2-node节点就是2-3树中的一个3-node节点了。

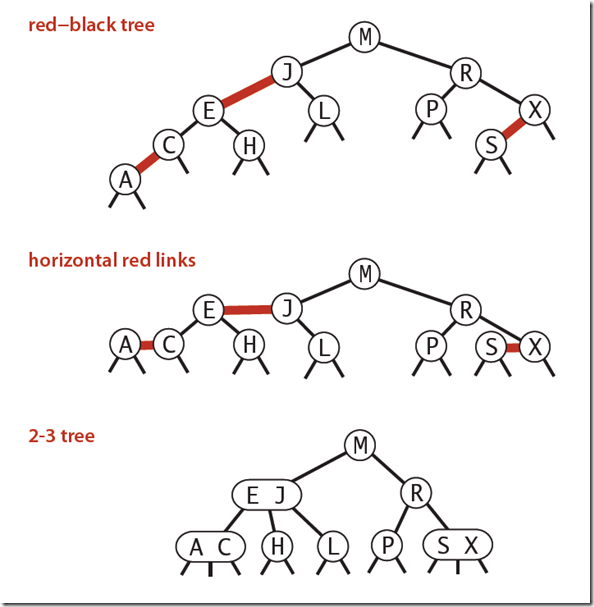
表示

我们可以在二叉查找树的每一个节点上增加一个新的表示颜色的标记。该标记指示该节点指向其父节点的颜色。

private const bool RED = true;
private const bool BLACK = false;

private Node root;

class Node
{
    public Node Left { get; set; }
    public Node Right { get; set; }
    public TKey Key { get; set; }
    public TValue Value { get; set; }
    public int Number { get; set; }
    public bool Color { get; set; }

    public Node(TKey key, TValue value,int number, bool color)
    {
        this.Key = key;
        this.Value = value;
        this.Number = number;
        this.Color = color;
    }
}

private bool IsRed(Node node)
{
    if (node == null) return false;
    return node.Color == RED;
}

实现

查找

红黑树是一种特殊的二叉查找树，他的查找方法也和二叉查找树一样，不需要做太多更改。

但是由于红黑树比一般的二叉查找树具有更好的平衡，所以查找起来更快。

//查找获取指定的值
public override TValue Get(TKey key)
{
    return GetValue(root, key);
}

private TValue GetValue(Node node, TKey key)
{
    if (node == null) return default(TValue);
    int cmp = key.CompareTo(node.Key);
    if (cmp == 0) return node.Value;
    else if (cmp > 0) return GetValue(node.Right, key);
    else return GetValue(node.Left, key);
}

平衡化

在介绍插入之前，我们先介绍如何让红黑树保持平衡，因为一般的，我们插入完成之后，需要对树进行平衡化操作以使其满足平衡化。

旋转

旋转又分为左旋和右旋。通常左旋操作用于将一个向右倾斜的红色链接旋转为向左链接。对比操作前后，可以看出，该操作实际上是将红线链接的两个节点中的一个较大的节点移动到根节点上。

左旋操作如下图：

 

//左旋转
private Node RotateLeft(Node h)
{
    Node x = h.Right;
    //将x的左节点复制给h右节点
    h.Right = x.Left;
    //将h复制给x右节点
    x.Left = h;
    x.Color = h.Color;
    h.Color = RED;
    return x;
}

左旋的动画效果如下：

右旋是左旋的逆操作，过程如下：

 

代码如下：

//右旋转
private Node RotateRight(Node h)
{
    Node x = h.Left;
    h.Left = x.Right;
    x.Right = h;

    x.Color = h.Color;
    h.Color = RED;
    return x;
}

右旋的动画效果如下：

颜色反转

当出现一个临时的4-node的时候，即一个节点的两个子节点均为红色，如下图：

 

这其实是个A，E，S 4-node连接，我们需要将E提升至父节点，操作方法很简单，就是把E对子节点的连线设置为黑色，自己的颜色设置为红色。

有了以上基本操作方法之后，我们现在对应之前对2-3树的平衡操作来对红黑树进行平衡操作，这两者是可以一一对应的，如下图：

现在来讨论各种情况：

Case 1 往一个2-node节点底部插入新的节点

先热身一下，首先我们看对于只有一个节点的红黑树，插入一个新的节点的操作：

这种情况很简单，只需要：

• 标准的二叉查找树遍历即可。新插入的节点标记为红色
• 如果新插入的节点在父节点的右子节点，则需要进行左旋操作

Case 2往一个3-node节点底部插入新的节点

先热身一下，假设我们往一个只有两个节点的树中插入元素，如下图，根据待插入元素与已有元素的大小，又可以分为如下三种情况：

• 如果带插入的节点比现有的两个节点都大，这种情况最简单。我们只需要将新插入的节点连接到右边子树上即可，然后将中间的元素提升至根节点。这样根节点的左右子树都是红色的节点了，我们只需要调研FlipColor方法即可。其他情况经过反转操作后都会和这一样。
• 如果插入的节点比最小的元素要小，那么将新节点添加到最左侧，这样就有两个连接红色的节点了，这是对中间节点进行右旋操作，使中间结点成为根节点。这是就转换到了第一种情况，这时候只需要再进行一次FlipColor操作即可。
• 如果插入的节点的值位于两个节点之间，那么将新节点插入到左侧节点的右子节点。因为该节点的右子节点是红色的，所以需要进行左旋操作。操作完之后就变成第二种情况了，再进行一次右旋，然后再调用FlipColor操作即可完成平衡操作。

有了以上基础，我们现在来总结一下往一个3-node节点底部插入新的节点的操作步骤，下面是一个典型的操作过程图：

可以看出，操作步骤如下：

1. 执行标准的二叉查找树插入操作，新插入的节点元素用红色标识。
2. 如果需要对4-node节点进行旋转操作
3. 如果需要，调用FlipColor方法将红色节点提升
4. 如果需要，左旋操作使红色节点左倾。
5. 在有些情况下，需要递归调用Case1 Case2，来进行递归操作。如下：

代码实现

经过上面的平衡化讨论，现在就来实现插入操作，一般地插入操作就是先执行标准的二叉查找树插入，然后再进行平衡化。对照2-3树，我们可以通过前面讨论的，左旋，右旋，FlipColor这三种操作来完成平衡化。

具体操作方式如下：

• 如果节点的右子节点为红色，且左子节点位黑色，则进行左旋操作
• 如果节点的左子节点为红色，并且左子节点的左子节点也为红色，则进行右旋操作
• 如果节点的左右子节点均为红色，则执行FlipColor操作，提升中间结点。

根据这一逻辑，我们就可以实现插入的Put方法了。

public override void Put(TKey key, TValue value)
{
    root = Put(root, key, value);
    root.Color = BLACK;
}

private Node Put(Node h, TKey key, TValue value)
{
    if (h == null) return new Node(key, value, 1, RED);
    int cmp = key.CompareTo(h.Key);
    if (cmp < 0) h.Left = Put(h.Left, key, value);
    else if (cmp > 0) h.Right = Put(h.Right, key, value);
    else h.Value = value;

    //平衡化操作
    if (IsRed(h.Right) && !IsRed(h.Left)) h = RotateLeft(h);
    if (IsRed(h.Right) && IsRed(h.Left.Left)) h = RotateRight(h);
    if (IsRed(h.Left) && IsRed(h.Right)) h = FlipColor(h);

    h.Number = Size(h.Left) + Size(h.Right) + 1;
    return h;
}

private int Size(Node node)
{
    if (node == null) return 0;
    return node.Number;
}

分析

对红黑树的分析其实就是对2-3查找树的分析，红黑树能够保证符号表的所有操作即使在最坏的情况下都能保证对数的时间复杂度，也就是树的高度。

在分析之前，为了更加直观，下面是以升序，降序和随机构建一颗红黑树的动画：

• 以升序插入构建红黑树：

• 以降序插入构建红黑树：

• 随机插入构建红黑树

从上面三张动画效果中，可以很直观的看出，红黑树在各种情况下都能维护良好的平衡性，从而能够保证最差情况下的查找，插入效率。

下面来详细分析下红黑树的效率：

1. 在最坏的情况下，红黑树的高度不超过2lgN

最坏的情况就是，红黑树中除了最左侧路径全部是由3-node节点组成，即红黑相间的路径长度是全黑路径长度的2倍。

下图是一个典型的红黑树，从中可以看到最长的路径(红黑相间的路径)是最短路径的2倍：

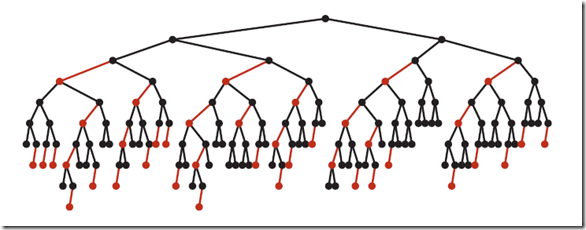
2. 红黑树的平均高度大约为lgN

下图是红黑树在各种情况下的时间复杂度，可以看出红黑树是2-3查找树的一种实现，他能保证最坏情况下仍然具有对数的时间复杂度。

下图是红黑树各种操作的时间复杂度。

应用

红黑树这种数据结构应用十分广泛，在多种编程语言中被用作符号表的实现，如：

• Java中的java.util.TreeMap,java.util.TreeSet
• C++ STL中的：map,multimap,multiset
• .NET中的：SortedDictionary,SortedSet 等

下面以.NET中为例，通过Reflector工具，我们可以看到SortedDictionary的Add方法如下：

public void Add(T item)
{
    if (this.root == null)
    {
        this.root = new Node<T>(item, false);
        this.count = 1;
    }
    else
    {
        Node<T> root = this.root;
        Node<T> node = null;
        Node<T> grandParent = null;
        Node<T> greatGrandParent = null;
        int num = 0;
        while (root != null)
        {
            num = this.comparer.Compare(item, root.Item);
            if (num == 0)
            {
                this.root.IsRed = false;
                ThrowHelper.ThrowArgumentException(ExceptionResource.Argument_AddingDuplicate);
            }
            if (TreeSet<T>.Is4Node(root))
            {
                TreeSet<T>.Split4Node(root);
                if (TreeSet<T>.IsRed(node))
                {
                    this.InsertionBalance(root, ref node, grandParent, greatGrandParent);
                }
            }
            greatGrandParent = grandParent;
            grandParent = node;
            node = root;
            root = (num < 0) ? root.Left : root.Right;
        }
        Node<T> current = new Node<T>(item);
        if (num > 0)
        {
            node.Right = current;
        }
        else
        {
            node.Left = current;
        }
        if (node.IsRed)
        {
            this.InsertionBalance(current, ref node, grandParent, greatGrandParent);
        }
        this.root.IsRed = false;
        this.count++;
        this.version++;
    }
}

可以看到，内部实现也是一个红黑树，其操作方法和本文将的大同小异，感兴趣的话，您可以使用Reflector工具跟进去查看源代码。

总结

前文讲解了自平衡查找树中的2-3查找树，这种数据结构在插入之后能够进行自平衡操作，从而保证了树的高度在一定的范围内进而能够保证最坏情况下的时间复杂度。但是2-3查找树实现起来比较困难，红黑树是2-3树的一种简单高效的实现，他巧妙地使用颜色标记来替代2-3树中比较难处理的3-node节点问题。红黑树是一种比较高效的平衡查找树，应用非常广泛，很多编程语言的内部实现都或多或少的采用了红黑树。

希望本文对您了解红黑树有所帮助，下文将介绍在文件系统以及数据库系统中应用非常广泛的另外一种平衡树结构：B树。

http://www.cnblogs.com/yangecnu/p/Introduce-B-Tree-and-B-Plus-Tree.html

http://www.cnblogs.com/yangecnu/p/Introduce-B-Tree-and-B-Plus-Tree.html

浅谈算法和数据结构: 十 平衡查找树之B树

 

前面讲解了平衡查找树中的2-3树以及其实现红黑树。2-3树种，一个节点最多有2个key，而红黑树则使用染色的方式来标识这两个key。

维基百科对B树的定义为“在计算机科学中，B树（B-tree）是一种树状数据结构，它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树，概括来说是一个节点可以拥有多于2个子节点的二叉查找树。与自平衡二叉查找树不同，B-树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程，从而加快存取速度。普遍运用在数据库和文件系统。”

定义

B 树可以看作是对2-3查找树的一种扩展，即他允许每个节点有M-1个子节点。

• 根节点至少有两个子节点
• 每个节点有M-1个key，并且以升序排列
• 位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间
• 其它节点至少有M/2个子节点

下图是一个M=4 阶的B树:

可以看到B树是2-3树的一种扩展，他允许一个节点有多于2个的元素。

B树的插入及平衡化操作和2-3树很相似，这里就不介绍了。下面是往B树中依次插入

6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4

的演示动画：

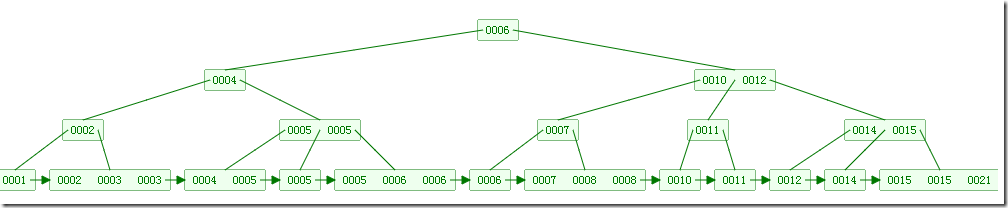
B+树是对B树的一种变形树，它与B树的差异在于：

• 有k个子结点的结点必然有k个关键码；
• 非叶结点仅具有索引作用，跟记录有关的信息均存放在叶结点中。
• 树的所有叶结点构成一个有序链表，可以按照关键码排序的次序遍历全部记录。

如下图，是一个B+树:

下图是B+树的插入动画：

B和B+树的区别在于，B+树的非叶子结点只包含导航信息，不包含实际的值，所有的叶子结点和相连的节点使用链表相连，便于区间查找和遍历。

B+ 树的优点在于：

• 由于B+树在内部节点上不好含数据信息，因此在内存页中能够存放更多的key。 数据存放的更加紧密，具有更好的空间局部性。因此访问叶子几点上关联的数据也具有更好的缓存命中率。
• B+树的叶子结点都是相链的，因此对整棵树的便利只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。

但是B树也有优点，其优点在于，由于B树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。下面是B 树和B+树的区别图：

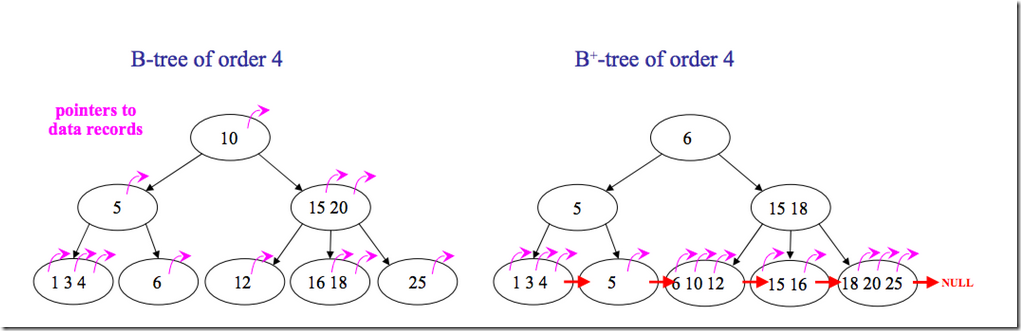
分析

对B树和B+树的分析和对前面讲解的2-3树的分析类似，

对于一颗节点为N度为M的子树，查找和插入需要log_M-1N ~ log_M/2N次比较。这个很好证明，对于度为M的B树，每一个节点的子节点个数为M/2 到 M-1之间，所以树的高度在log_M-1N至log_M/2N之间。

这种效率是很高的，对于N=62*1000000000个节点，如果度为1024，则log_M/2N <=4，即在620亿个元素中，如果这棵树的度为1024，则只需要小于4次即可定位到该节点，然后再采用二分查找即可找到要找的值。

应用

B树和B+广泛应用于文件存储系统以及数据库系统中，在讲解应用之前，我们看一下常见的存储结构：

我们计算机的主存基本都是随机访问存储器(Random-Access Memory，RAM)，他分为两类：静态随机访问存储器（SRAM）和动态随机访问存储器（DRAM）。SRAM比DRAM快，但是也贵的多，一般作为CPU的高速缓存，DRAM通常作为内存。这类存储器他们的结构和存储原理比较复杂，基本是使用电信号来保存信息的，不存在机器操作，所以访问速度非常快，具体的访问原理可以查看CSAPP，另外，他们是易失的，即如果断电，保存DRAM和SRAM保存的信息就会丢失。

我们使用的更多的是使用磁盘，磁盘能够保存大量的数据，从GB一直到TB级，但是 他的读取速度比较慢，因为涉及到机器操作，读取速度为毫秒级，从DRAM读速度比从磁盘度快10万倍，从SRAM读速度比从磁盘读快100万倍。下面来看下磁盘的结构：

如上图，磁盘由盘片构成,每个盘片有两面，又称为盘面(Surface)，这些盘面覆盖有磁性材料。盘片中央有一个可以旋转的主轴(spindle)，他使得盘片以固定的旋转速率旋转，通常是5400转每分钟(Revolution Per Minute,RPM)或者是7200RPM。磁盘包含一个多多个这样的盘片并封装在一个密封的容器内。上图左，展示了一个典型的磁盘表面结构。每个表面是由一组成为磁道(track)的同心圆组成的，每个磁道被划分为了一组扇区(sector).每个扇区包含相等数量的数据位，通常是（512）子节。扇区之间由一些间隔(gap)隔开,不存储数据。

以上是磁盘的物理结构，现在来看下磁盘的读写操作：

如上图，磁盘用读/写头来读写存储在磁性表面的位，而读写头连接到一个传动臂的一端。通过沿着半径轴前后移动传动臂，驱动器可以将读写头定位到任何磁道上，这称之为寻道操作。一旦定位到磁道后，盘片转动，磁道上的每个位经过磁头时，读写磁头就可以感知到位的值，也可以修改值。对磁盘的访问时间分为 寻道时间，旋转时间，以及传送时间。

由于存储介质的特性，磁盘本身存取就比主存慢很多，再加上机械运动耗费，因此为了提高效率，要尽量减少磁盘I/O，减少读写操作。为了达到这个目的，磁盘往往不是严格按需读取，而是每次都会预读，即使只需要一个字节，磁盘也会从这个位置开始，顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理：

当一个数据被用到时，其附近的数据也通常会马上被使用。

程序运行期间所需要的数据通常比较集中。

由于磁盘顺序读取的效率很高（不需要寻道时间，只需很少的旋转时间），因此对于具有局部性的程序来说，预读可以提高I/O效率。

预读的长度一般为页（page）的整倍数。页是计算机管理存储器的逻辑块，硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块，每个存储块称为一页（在许多操作系统中，页得大小通常为4k），主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时，会触发一个缺页异常，此时系统会向磁盘发出读盘信号，磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中，然后异常返回，程序继续运行。

文件系统及数据库系统的设计者利用了磁盘预读原理，将一个节点的大小设为等于一个页，这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的，在实际实现B-Tree还需要使用如下技巧：

每次新建一个节点的同时，直接申请一个页的空间( 512或者1024)，这样就保证一个节点物理上也存储在一个页里，加之计算机存储分配都是按页对齐的，就实现了一个node只需一次I/O。如，将B树的度M设置为1024，这样在前面的例子中，600亿个元素中只需要小于4次查找即可定位到某一存储位置。

同时在B+树中，内节点只存储导航用到的key，并不存储具体值，这样内节点个数较少，能够全部读取到主存中，外接点存储key及值，并且顺序排列，具有良好的空间局部性。所以B及B+树比较适合与文件系统的数据结构。下面是一颗B树，用来进行内容存储。

另外B/B+树也经常用做数据库的索引，这方面推荐您直接看张洋的MySQL索引背后的数据结构及算法原理 这篇文章，这篇文章对MySQL中的如何使用B+树进行索引有比较详细的介绍，推荐阅读。

总结

在前面两篇文章介绍了平衡查找树中的2-3树，红黑树之后，本文介绍了文件系统和数据库系统中常用的B/B+ 树，他通过对每个节点存储个数的扩展，使得对连续的数据能够进行较快的定位和访问，能够有效减少查找时间，提高存储的空间局部性从而减少IO操作。他广泛用于文件系统及数据库中，如：

• Windows：HPFS文件系统
• Mac：HFS，HFS+文件系统
• Linux：ResiserFS，XFS，Ext3FS，JFS文件系统
• 数据库：ORACLE，MYSQL，SQLSERVER等中

希望本文对您了解B/B+ 树有所帮助。