数据结构-AVL树的旋转
http://blog.csdn.net/GabrieL1026/article/details/6311339
平衡二叉树在进行插入操作的时候可能出现不平衡的情况,AVL树即是一种自平衡的二叉树,它通过旋转不平衡的节点来使二叉树重新保持平衡,并且查找、插入和删除操作在平均和最坏情况下时间复杂度都是O(log n)
AVL树的旋转一共有四种情形,注意所有旋转情况都是围绕着使得二叉树不平衡的第一个节点展开的。
1. LL型
平衡二叉树某一节点的左孩子的左子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向右旋转一次即可,如图所示,原A的左孩子B变为父结点,A变为其右孩子,而原B的右子树变为A的左子树,注意旋转之后Brh是A的左子树(图上忘在A于Brh之间标实线)
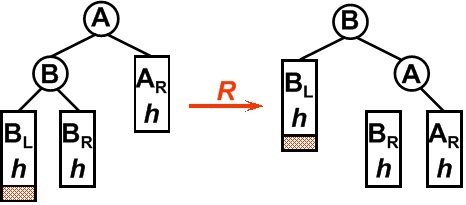
2. RR型
平衡二叉树某一节点的右孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向左旋转一次即可,如图所示,原A右孩子B变为父结点,A变为其左孩子,而原B的左子树Blh将变为A的右子树。
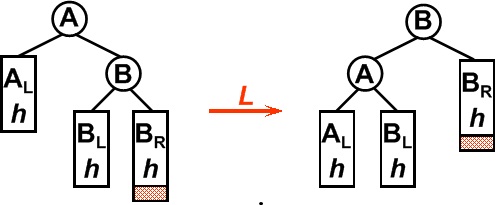
3. LR型
平衡二叉树某一节点的左孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时需要旋转两次,仅一次的旋转是不能够使二叉树再次平衡。如图所示,在B节点按照RR型向左旋转一次之后,二叉树在A节点仍然不能保持平衡,这时还需要再向右旋转一次。
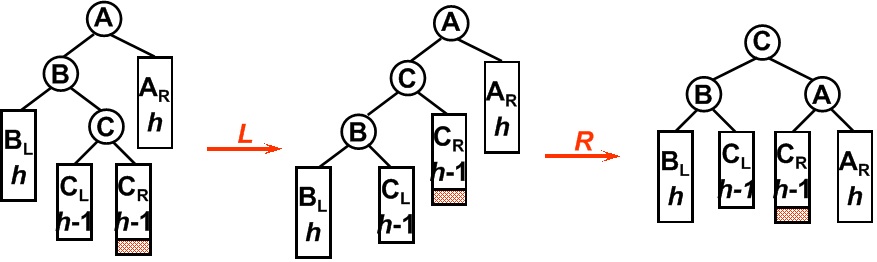
4. RL型
平衡二叉树某一节点的右孩子的左子树上插入一个新的节点,使得该节点不再平衡。同样,这时需要旋转两次,旋转方向刚好同LR型相反。
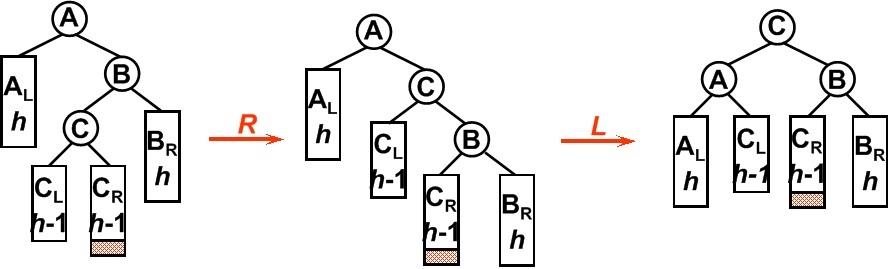
数据结构-AVL树的旋转的更多相关文章
- AVL树的JAVA实现及AVL树的旋转算法
1,AVL树又称平衡二叉树,它首先是一颗二叉查找树,但在二叉查找树中,某个结点的左右子树高度之差的绝对值可能会超过1,称之为不平衡.而在平衡二叉树中,任何结点的左右子树高度之差的绝对值会小于等于 1. ...
- AVL树平衡旋转详解
AVL树平衡旋转详解 概述 AVL树又叫做平衡二叉树.前言部分我也有说到,AVL树的前提是二叉排序树(BST或叫做二叉查找树).由于在生成BST树的过程中可能会出现线型树结构,比如插入的顺序是:1, ...
- Java数据结构——AVL树
AVL树(平衡二叉树)定义 AVL树本质上是一颗二叉查找树,但是它又具有以下特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,并且拥有自平衡机制.在AV ...
- AVL树的旋转
平衡二叉树在进行插入操作的时候可能出现不平衡的情况,AVL树即是一种自平衡的二叉树,它通过旋转不平衡的节点来使二叉树重新保持平衡,并且查找.插入和删除操作在平均和最坏情况下时间复杂度都是O(log n ...
- AVL树的旋转操作详解
[0]README 0.0) 本文部分idea 转自:http://blog.csdn.net/collonn/article/details/20128205 0.1) 本文仅针对性地分析AVL树的 ...
- JAVA数据结构--AVL树的实现
AVL树的定义 在计算机科学中,AVL树是最先发明的自平衡二叉查找树.在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下的时间复杂度都是.增 ...
- 数据结构--Avl树的创建,插入的递归版本和非递归版本,删除等操作
AVL树本质上还是一棵二叉搜索树,它的特点是: 1.本身首先是一棵二叉搜索树. 2.带有平衡条件:每个结点的左右子树的高度之差的绝对值最多为1(空树的高度为-1). 也就是说,AVL树,本质上 ...
- 再回首数据结构—AVL树(二)
前面主要介绍了AVL的基本概念与结构,下面开始详细介绍AVL的实现细节: AVL树实现的关键点 AVL树与二叉搜索树结构类似,但又有些细微的区别,从上面AVL树的介绍我们知道它需要维护其左右节点平衡, ...
- 第三十二篇 玩转数据结构——AVL树(AVL Tree)
1.. 平衡二叉树 平衡二叉树要求,对于任意一个节点,左子树和右子树的高度差不能超过1. 平衡二叉树的高度和节点数量之间的关系也是O(logn) 为二叉树标注节点高度并计算平衡因子 AVL ...
随机推荐
- Nexus中自定义私服,每个项目都用独立的工厂,仓库
原文:http://blog.csdn.net/mexican_jacky/article/details/50278045 第一步:创建工厂仓库 第二步:cms项目,那么我们就只能cms项目组用,那 ...
- 转:Jeff Atwood倾情推荐——程序员必读之书
Jeff Atwood倾情推荐——程序员必读之书 英文版:<Code Complete 2>中文版:<代码大全(第二版)>作者:Steve McConnell译者:金戈 汤凌 ...
- Lucene 基础理论 (zhuan)
http://www.blogjava.net/hoojo/archive/2012/09/06/387140.html**************************************** ...
- UnicodeEncodeError
UnicodeEncodeError at /admin/shop/product/add/ 'ascii' codec can't encode characters in position 0-1 ...
- association ,collection
mybatis 出现这个错误Error creating document instance. Cause: org.xml.sax.SAXParseException; lineNumber: 2 ...
- js简单模仿队列
window.meng = window.meng || {}; (function () { var items = []; meng.queue = { /** * * @param {Funct ...
- Wifi-Direct
参考链接:http://developer.android.com/guide/topics/connectivity/wifip2p.html 国内镜像开发文档:http://wear.techbr ...
- tr设置背景图片
tr是不能设置背景图片的....
- vs版本的改变处理
今天要用VS2010打开VS2013,一直觉得VS2010到VS2012只是界面上扁平化的改变,平台工具集有改变但很大程度上可能向上兼容.在网上搜了一些文章,其中有一篇说到一个观点: 从 ...
- Shell基础:Linux权限管理
Linux权限基本概念 查看系统(文件夹/文件)权限: ls -l =>d/- xxx xxx xxx. num owner group size date filename ...
