NOIP 2016 蚯蚓 (luogu 2827 & uoj 264)

题目描述

本题中，我们将用符号\lfloor c \rfloor⌊c⌋表示对c向下取整，例如：\lfloor 3.0 \rfloor= \lfloor 3.1 \rfloor=\lfloor 3.9 \rfloor=3⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。

蛐蛐国最近蚯蚓成灾了！隔壁跳蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。

蛐蛐国里现在共有n只蚯蚓（n为正整数)。每只蚯蚓拥有长度，我们设第i只蚯蚓的长度为a_i(i=1,2,...,n)ai(i=1,2,...,n)，并保证所有的长度都是非负整数（即:可能存在长度为0的蚯蚓）。

每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）将其切成两半。神刀手切开蚯蚓的位置由常数p(是满足0<p<1的有理数)决定，设这只蚯蚓长度为x，神刀手会将其切成两只长度分别为\lfloor px \rfloor⌊px⌋和x-\lfloor px \rfloorx−⌊px⌋的蚯蚓。特殊地，如果这两个数的其中一个等于0，则这个长度为0的蚯蚓也会被保留。此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加q(是一个非负整常数)。

蛐蛐国王知道这样不是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要m秒才能到来......

(m为非负整数）

蛐蛐国王希望知道这m秒内的战况。具体来说，他希望知道：

•m秒内，每一秒被切断的蚯蚓被切断前的长度（有m个数）

•m秒后，所有蚯蚓的长度（有n+m个数)。

蛐蛐国王当然知道怎么做啦！但是他想考考你......

输入输出格式

输入格式：

第一行包含六个整数n,m,q,u,v,t，其中：n,m,q的意义见【问题描述】；u,v,t均为正整数；你需要自己计算p=u/v(保证0<u<v)t是输出参数，其含义将会在【输出格式】中解释。

第二行包含n个非负整数，为a_i,a_2,...,a_nai,a2,...,an，即初始时n只蚯蚓的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。

保证1 \le n \le 10^51≤n≤105，0<m \le 7*10^60<m≤7∗106，0 \le u<v \le 10^90≤u<v≤109，0 \le q \le 2000≤q≤200，1 \le t \le 711≤t≤71，0<ai \le 10^80<ai≤108。

输出格式：

第一行输出\lfloor m/t \rfloor⌊m/t⌋个整数，按时间顺序，依次输出第t秒，第2t秒，第3t秒……被切断蚯蚓（在被切断前）的长度。

第二行输出\lfloor (n+m)/t \rfloor⌊(n+m)/t⌋个整数，输出m秒后蚯蚓的长度；需要按从大到小的顺序，依次输出排名第t，第2t，第3t……的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

输入输出样例

输入样例#1：复制

3 7 1 1 3 1
3 3 2

输出样例#1：复制

3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2

输入样例#2：复制

3 7 1 1 3 2
3 3 2

输出样例#2：复制

4 4 5
6 5 4 3 2

输入样例#3：复制

3 7 1 1 3 9
3 3 2

输出样例#3：复制

//空行
2

说明

【样例解释1】

在神刀手到来前：3只蚯蚓的长度为3,3,2。

1秒后：一只长度为3的蚯蚓被切成了两只长度分别为1和2的蚯蚓，其余蚯蚓的长度增加了1。最终4只蚯蚓的长度分别为(1,2),4,3。括号表示这个位置刚刚有一只蚯蚓被切断

2秒后：一只长度为4的蚯蚓被切成了1和3。5只蚯蚓的长度分别为：2,3,(1,3),4。

3秒后：一只长度为4的蚯蚓被切断。6只蚯蚓的长度分别为：3,4,2,4,(1,3)。

4秒后：一只长度为4的蚯蚓被切断。7只蚯蚓的长度分别为：4,(1,3),3,5,2,4。

5秒后：一只长度为5的蚯蚓被切断。8只蚯蚓的长度分别为：5,2,4,4,(1,4),3,5。

6秒后：一只长度为5的蚯蚓被切断。9只蚯蚓的长度分别为：（1,4),3,5,5,2,5,4,6。

7秒后：一只长度为6的蚯蚓被切断。10只蚯蚓的长度分别为：2,5,4,6,6,3,6,5,(2,4)。所以，7秒内被切断的蚯蚓的长度依次为3,4,4,4,5,5,6。7秒后，所有蚯蚓长度从大到小排序为6,6,6,5,5,4,4,3,2,2

【样例解释2】

这个数据中只有t=2与上个数据不同。只需在每行都改为每两个数输出一个数即可。

虽然第一行最后有一个6没有被输出，但是第二行仍然要重新从第二个数再开始输出。

【样例解释3】

这个数据中只有t=9与上个数据不同。

注意第一行没有数要输出，但也要输出一个空行。

【数据范围】

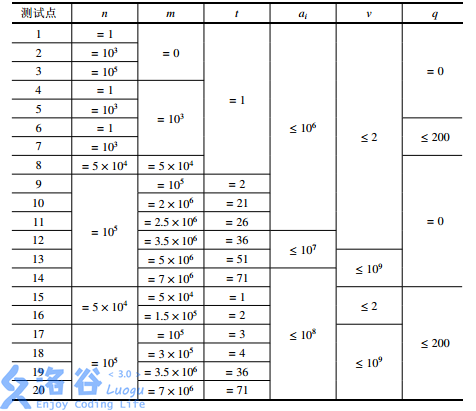
　　题目大意 (题目太简洁不需要大意)

　　分析题目，不难得到下面两个性质:

　　1.长的蚯蚓总是比短的先被切。

　　2.长的蚯蚓切成的长短两半分别比短的蚯蚓切成的长短两半长。

　　根据第2点性质，可以考虑用队列维护切成的长、短蚯蚓，这样能够保证从队尾到队首是不减的。

　　然后再根据第1点性质，考虑取出所有队列中的最大值。

　　然后会出现一个问题，就是原始的蚯蚓放在哪个队列里呢？很遗憾的是上述两个队列都不放它。而是将它排序后，重新开一个队列存它。

　　然后是题目本身带来的问题:如何整体增加？

　　可以发现不增加的蚯蚓每次只有2只，所以考虑将整体增加变为个体减少。

　　但是切蚯蚓的时候，需要先将增加的值加回去，然后再切，最后把增加的值都减回去。

Code

 /**
  * luogu
  * Problem#2827
  * Accepted
  * Time: 1960ms
  * Memory: 57292k
  */
 #include <bits/stdc++.h>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;
 typedef bool boolean;
 const signed int inf = (signed)((~0u) >> );
 #define smax(_a, _b) _a = max(_a, _b)
 #define smin(_a, _b) _a = min(_a, _b)
 
 int n, m, Q, u, v, t;
 int* a;
 
 inline void init() {
     scanf("%d%d%d%d%d%d", &n, &m, &Q, &u, &v, &t);
     a = new int[(n + m + )];
     for(int i = ; i <= n; i++)
         scanf("%d", a + i);
 }
 
 queue<int> q[];
 
 int getMaxid() {
     int rt = , maxv = -inf;
     for(int i = ; i < ; i++)
         if(!q[i].empty() && q[i].front() > maxv)
             rt = i, maxv = q[i].front();
     return rt;
 }
 
 inline void solve() {
     sort(a + , a + n + , greater<int>());
     for(int i = ; i <= n; i++)
         q[].push(a[i]);
 
     long long added = ;
     long long val1, val2;
     for(int t = , id; t <= m; t++, added += Q) {
         id = getMaxid();
         val1 = q[id].front() + added;
         q[id].pop();
         if((t % ::t) == )
             printf(Auto" ", val1);
         val2 = val1 * 1ll * u / v;
         q[].push(val2 - Q - added);
         q[].push(val1 - val2 - Q - added);
     }
     putchar('\n');
 
     int cnt = , id;
     while(!q[].empty() || !q[].empty() || !q[].empty()) {
         id = getMaxid();
         a[cnt++] = q[id].front();
         q[id].pop();
     }
     for(int i = ::t; i < cnt; i += ::t)
         printf(Auto" ", a[i] + Q * 1ll * m);
 }
 
 int main() {
     init();
     solve();
     return ;
 }