[luogu P3382] 三分法

[luogu P3382] 三分法

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

输出格式：

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

输入输出样例

输入样例#1：

3 -0.9981 0.5
1 -3 -3 1

输出样例#1：

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

样例说明：

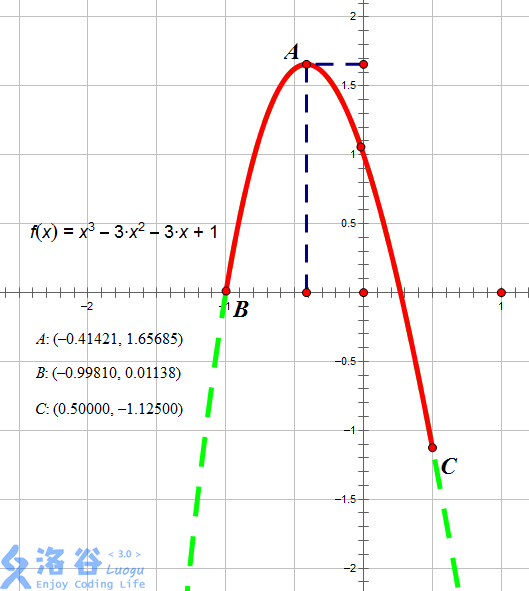
如图所示，红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。

当x=-0.41421时图像位于最高点，故此时函数在[l,x]上单调增，[x,r]上单调减，故x=-0.41421，输出-0.41421。

疯狂学习杂七杂八的算法。。。

三分和二分差不多，二分就是有一个中间端点，三分有两个。

为什么会有两个呢？因为三分主要是对于那些在某一段区间先升后降或先降后升的问题，有个最高或最低点。

三分的一贯写法：

 while (L<=R) {
     lm=L+(R-L)/,rm=R-(R-L)/;
     if (calc(lm)>calc(rm)) L=Lm; else R=Rm;
 }

其中里面的if要视情况而定（也就是有最低点还是最高点）。

code：

 #include<bits/stdc++.h>
 #define DB double
 using namespace std;
 ;
 ];
 DB ca(DB x) {
     DB ret=;
     ; i--) ret=ret*x+a[i];
     return ret;
 }
 int main() {
     scanf("%d%lf%lf",&n,&L,&R);
     ; i--) scanf("%lf",&a[i]);
     while (R-L>=eps) {
         m=(R-L)/,lm=m+L,rm=R-m;
         lv=ca(lm);
         rv=ca(rm);
         if (ca(lm)<ca(rm)) L=lm; else R=rm;
     }
     printf("%.5lf",L);
     ;
 }