ACM/ICPC 之 DP进阶(51Nod-1371(填数字))

原题链接：填数字

顺便推荐一下，偶然看到这个OJ，发现社区运营做得很赞，而且交互和编译环境都很赞(可以编译包括Python,Ruby，Js在内的脚本语言，也可以编译新标准的C/C++11，甚至包括Go和C Sharp等)，虽然暂时不太火，但估计会逐渐成为国内算法界非常受欢迎的OJ社区。

主页：http://www.51nod.com/index.html

---

　　

　　本题是个题意简单的，思路复杂的DP题，说实话，光是想出这种DP就已经非常不易了，即便写出来也要考虑清楚每一种转移的公式和数值关系。

　　

　　原题：有n(1-200)行格子，第i(1<=i<=n)行有i个格子，每行格子是左对齐。现在要在每一个格子填入一个非负整数，最后使得每一行每一列的和都不超过2。

　　　　　请计算有多少种方案，答案比较大，请输出对100,000,007(1e8+7)取余后的结果。

　　　　　下图是n=4的时候格子的摆放。

　　　　　　

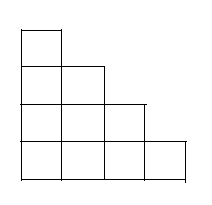
 //务必注意理清每次状态转移方程的思路和公式
 //博主因为一个地方写多了个+1，结果WA了5发....
 //Memory:34900K Time:93Ms
 #include<iostream>
 using namespace std;

 #define MAX 201
 #define MOD 100000007

 #define COL_0 (i - j - k - 1)    //和为0的列数
 /*
 * dp[i][j][k]
 * i:表明当前行
 * j:表明i行完成时有多少列为1
 * k:表明j行完成时有多少列为2
 * dp值表明该状态下的情况数
 * 每次由 i-1行 -> i行 转移同j同k的状态
 */
 __int64 dp[MAX][MAX][MAX];

 int main()
 {
     int n;
     scanf("%d", &n);
     dp[][][] = dp[][][] = dp[][][] = ;
     for (__int64 i = ; i <= n; i++)
         for (__int64 j = ; j <= i; j++)
             for (__int64 k = ; k <= i - j; k++)
             {
                 //最后一格为0时
                 //-可+2
                 if (i - j - k -  >= )
                     dp[i][j][k + ] = (dp[i][j][k + ] + dp[i - ][j][k] * COL_0) % MOD;
                 //-可+1
                 //--两个1_0-0
                 if (i - j - k -  >= )
                     dp[i][j + ][k] = (dp[i][j + ][k] + dp[i - ][j][k] * (COL_0 * (COL_0 - ) / )) % MOD;
                 //--两个1_1-0
                 if (j >=  && i - j - k -  >= )
                     dp[i][j][k + ] = (dp[i][j][k + ] + dp[i - ][j][k] * COL_0 *j) % MOD;
                 //--两个1_1-1
                 if (j >= )
                     dp[i][j - ][k + ] = (dp[i][j - ][k + ] + dp[i - ][j][k] * (j*(j - ) / )) % MOD;
                 //--一个1_1
                 if (j >= )
                     dp[i][j - ][k + ] = (dp[i][j - ][k + ] + dp[i - ][j][k] * j) % MOD;
                 //--一个1_0
                 if (i - j - k -  >= )
                     dp[i][j + ][k] = (dp[i][j + ][k] + dp[i - ][j][k] * COL_0) % MOD;
                 //什么都不加
                 dp[i][j][k] = (dp[i][j][k] + dp[i - ][j][k]) % MOD;

                 //最后一格为1时
                 //-可+1_0
                 if (i - j - k -  >= )
                     dp[i][j + ][k] = (dp[i][j + ][k] + dp[i - ][j][k] * COL_0) % MOD;
                 //-可+1_1
                 if (j >= )
                     dp[i][j][k + ] = (dp[i][j][k + ] + dp[i - ][j][k] * j) % MOD;
                 //什么都不加
                 dp[i][j + ][k] = (dp[i][j + ][k] + dp[i - ][j][k]) % MOD;

                 //最后一格为2时
                 dp[i][j][k + ] = (dp[i][j][k + ] + dp[i - ][j][k]) % MOD;
             }

     __int64 sum = ;
     for (int j = ; j <= n; j++)
         for (int k = ; k <= n - j; k++)
             sum = (sum + dp[n][j][k]) % MOD;
     printf("%I64d\n", sum);

     return ;
 }