SVM之SMO最小序列
转载自:JerryLead
http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988419.html
11 SMO优化算法(Sequential minimal optimization)
SMO算法由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规划优化算法,特别针对线性SVM和数据稀疏时性能更优。关于SMO最好的资料就是他本人写的《Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines》了。
我拜读了一下,下面先说讲义上对此方法的总结。
首先回到我们前面一直悬而未解的问题,对偶函数最后的优化问题:
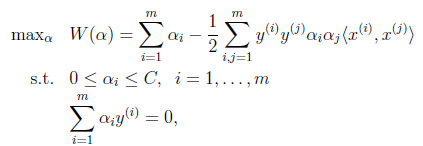
要解决的是在参数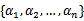 上求最大值W的问题,至于
上求最大值W的问题,至于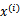 和
和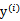 都是已知数。C由我们预先设定,也是已知数。
都是已知数。C由我们预先设定,也是已知数。
按照坐标上升的思路,我们首先固定除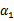 以外的所有参数,然后在
以外的所有参数,然后在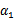 上求极值。等一下,这个思路有问题,因为如果固定
上求极值。等一下,这个思路有问题,因为如果固定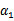 以外的所有参数,那么
以外的所有参数,那么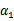 将不再是变量(可以由其他值推出),因为问题中规定了
将不再是变量(可以由其他值推出),因为问题中规定了
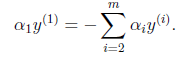
因此,我们需要一次选取两个参数做优化,比如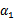 和
和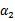 ,此时
,此时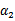 可以由
可以由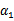 和其他参数表示出来。这样回带到W中,W就只是关于
和其他参数表示出来。这样回带到W中,W就只是关于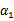 的函数了,可解。
的函数了,可解。
这样,SMO的主要步骤如下:

意思是,第一步选取一对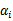 和
和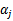 ,选取方法使用启发式方法(后面讲)。第二步,固定除
,选取方法使用启发式方法(后面讲)。第二步,固定除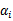 和
和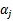 之外的其他参数,确定W极值条件下的
之外的其他参数,确定W极值条件下的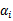 ,
,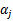 由
由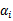 表示。
表示。
SMO之所以高效就是因为在固定其他参数后,对一个参数优化过程很高效。
下面讨论具体方法:
假设我们选取了初始值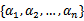 满足了问题中的约束条件。接下来,我们固定
满足了问题中的约束条件。接下来,我们固定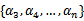 ,这样W就是
,这样W就是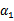 和
和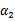 的函数。并且
的函数。并且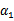 和
和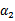 满足条件:
满足条件:
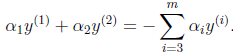
由于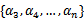 都是已知固定值,因此为了方面,可将等式右边标记成实数值
都是已知固定值,因此为了方面,可将等式右边标记成实数值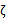 。
。
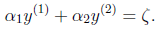
当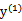 和
和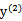 异号时,也就是一个为1,一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
异号时,也就是一个为1,一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
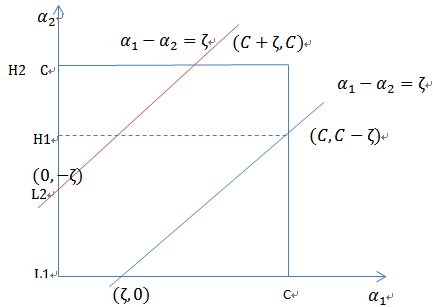
横轴是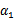 ,纵轴是
,纵轴是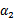 ,
,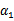 和
和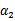 既要在矩形方框内,也要在直线上,因此
既要在矩形方框内,也要在直线上,因此
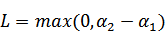 ,
,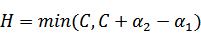
同理,当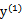 和
和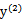 同号时,
同号时,
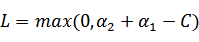 ,
,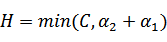
然后我们打算将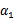 用
用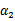 表示:
表示:
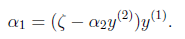
然后反代入W中,得
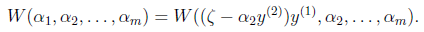
展开后W可以表示成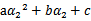 。其中a,b,c是固定值。这样,通过对W进行求导可以得到
。其中a,b,c是固定值。这样,通过对W进行求导可以得到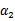 ,然而要保证
,然而要保证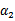 满足
满足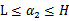 ,我们使用
,我们使用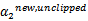 表示求导求出来的
表示求导求出来的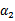 ,然而最后的
,然而最后的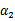 ,要根据下面情况得到:
,要根据下面情况得到:
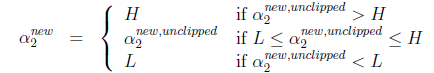
这样得到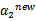 后,我们可以得到
后,我们可以得到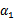 的新值
的新值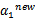 。
。
下面进入Platt的文章,来找到启发式搜索的方法和求b值的公式。
这边文章使用的符号表示有点不太一样,不过实质是一样的,先来熟悉一下文章中符号的表示。
文章中定义特征到结果的输出函数为

与我们之前的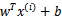 实质是一致的。
实质是一致的。
原始的优化问题为:
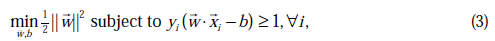
求导得到:

经过对偶后为:
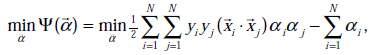
s.t. 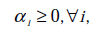
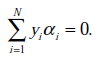
这里与W函数是一样的,只是符号求反后,变成求最小值了。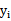 和
和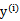 是一样的,都表示第i个样本的输出结果(1或-1)。
是一样的,都表示第i个样本的输出结果(1或-1)。
经过加入松弛变量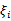 后,模型修改为:
后,模型修改为:
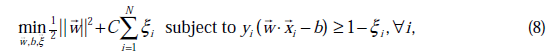

由公式(7)代入(1)中可知,

这个过程和之前对偶过程一样。
重新整理我们要求的问题为:
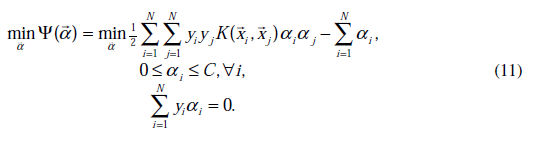
与之对应的KKT条件为:

这个KKT条件说明,在两条间隔线外面的点,对应前面的系数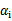 为0,在两条间隔线里面的对应
为0,在两条间隔线里面的对应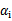 为C,在两条间隔线上的对应的系数
为C,在两条间隔线上的对应的系数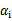 在0和C之间。
在0和C之间。
将我们之前得到L和H重新拿过来:
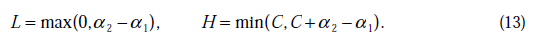
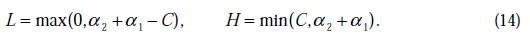
之前我们将问题进行到这里,然后说将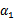 用
用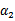 表示后代入W中,这里将代入
表示后代入W中,这里将代入 中,得
中,得
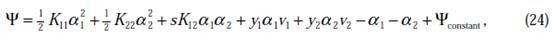
其中
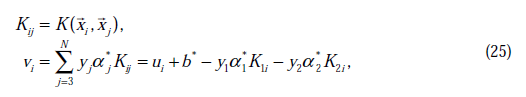
这里的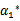 和
和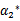 代表某次迭代前的原始值,因此是常数,而
代表某次迭代前的原始值,因此是常数,而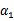 和
和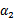 是变量,待求。公式(24)中的最后一项是常数。
是变量,待求。公式(24)中的最后一项是常数。
由于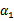 和
和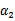 满足以下公式
满足以下公式
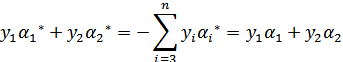
因为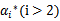 的值是固定值,在迭代前后不会变。
的值是固定值,在迭代前后不会变。
那么用s表示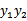 ,上式两边乘以
,上式两边乘以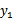 时,变为:
时,变为:

其中
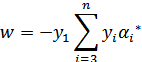
代入(24)中,得
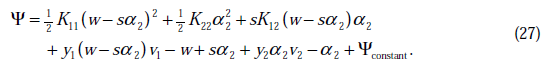
这时候只有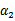 是变量了,求导
是变量了,求导
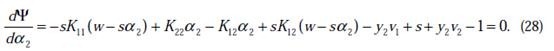
如果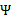 的二阶导数大于0(凹函数),那么一阶导数为0时,就是极小值了。
的二阶导数大于0(凹函数),那么一阶导数为0时,就是极小值了。
假设其二阶导数为0(一般成立),那么上式化简为:
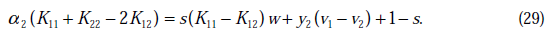
将w和v代入后,继续化简推导,得(推导了六七行推出来了)
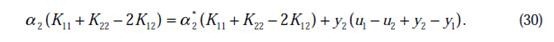
我们使用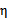 来表示:
来表示:
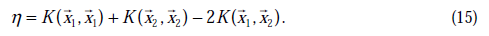
通常情况下目标函数是正定的,也就是说,能够在直线约束方向上求得最小值,并且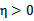 。
。
那么我们在(30)两边都除以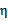 可以得到
可以得到

这里我们使用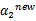 表示优化后的值,
表示优化后的值,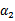 是迭代前的值,
是迭代前的值,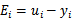 。
。
与之前提到的一样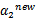 不是最终迭代后的值,需要进行约束:
不是最终迭代后的值,需要进行约束:
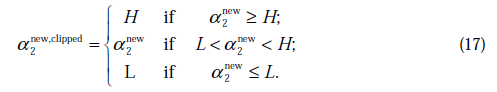
那么
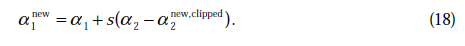
在特殊情况下,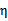 可能不为正,如果核函数K不满足Mercer定理,那么目标函数可能变得非正定,
可能不为正,如果核函数K不满足Mercer定理,那么目标函数可能变得非正定,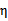 可能出现负值。即使K是有效的核函数,如果训练样本中出现相同的特征x,那么
可能出现负值。即使K是有效的核函数,如果训练样本中出现相同的特征x,那么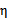 仍有可能为0。SMO算法在
仍有可能为0。SMO算法在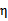 不为正值的情况下仍有效。为保证有效性,我们可以推导出
不为正值的情况下仍有效。为保证有效性,我们可以推导出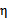 就是
就是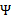 的二阶导数,
的二阶导数,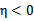 ,
,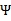 没有极小值,最小值在边缘处取到(类比
没有极小值,最小值在边缘处取到(类比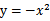 ),
),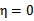 时更是单调函数了,最小值也在边缘处取得,而
时更是单调函数了,最小值也在边缘处取得,而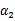 的边缘就是L和H。这样将
的边缘就是L和H。这样将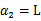 和
和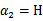 分别代入
分别代入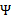 中即可求得
中即可求得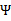 的最小值,相应的
的最小值,相应的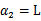 还是
还是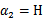 也可以知道了。具体计算公式如下:
也可以知道了。具体计算公式如下:
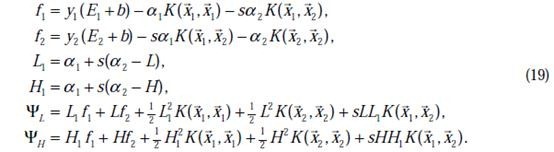
至此,迭代关系式出了b的推导式以外,都已经推出。
b每一步都要更新,因为前面的KKT条件指出了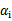 和
和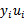 的关系,而
的关系,而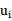 和b有关,在每一步计算出
和b有关,在每一步计算出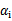 后,根据KKT条件来调整b。
后,根据KKT条件来调整b。
b的更新有几种情况:

来自罗林开的ppt
这里的界内指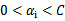 ,界上就是等于0或者C了。
,界上就是等于0或者C了。
前面两个的公式推导可以根据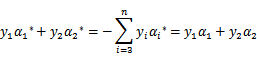
和对于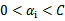 有
有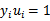 的KKT条件推出。
的KKT条件推出。
这样全部参数的更新公式都已经介绍完毕,附加一点,如果使用的是线性核函数,我们就可以继续使用w了,这样不用扫描整个样本库来作内积了。
w值的更新方法为:
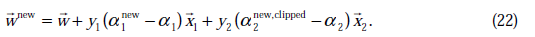
根据前面的

公式推导出。
12 SMO中拉格朗日乘子的启发式选择方法
终于到了最后一个问题了,所谓的启发式选择方法主要思想是每次选择拉格朗日乘子的时候,优先选择样本前面系数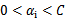 的
的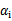 作优化(论文中称为无界样例),因为在界上(
作优化(论文中称为无界样例),因为在界上(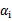 为0或C)的样例对应的系数
为0或C)的样例对应的系数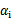 一般不会更改。
一般不会更改。
这条启发式搜索方法是选择第一个拉格朗日乘子用的,比如前面的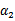 。那么这样选择的话,是否最后会收敛。可幸的是Osuna定理告诉我们只要选择出来的两个
。那么这样选择的话,是否最后会收敛。可幸的是Osuna定理告诉我们只要选择出来的两个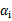 中有一个违背了KKT条件,那么目标函数在一步迭代后值会减小。违背KKT条件不代表
中有一个违背了KKT条件,那么目标函数在一步迭代后值会减小。违背KKT条件不代表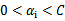 ,在界上也有可能会违背。是的,因此在给定初始值
,在界上也有可能会违背。是的,因此在给定初始值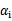 =0后,先对所有样例进行循环,循环中碰到违背KKT条件的(不管界上还是界内)都进行迭代更新。等这轮过后,如果没有收敛,第二轮就只针对
=0后,先对所有样例进行循环,循环中碰到违背KKT条件的(不管界上还是界内)都进行迭代更新。等这轮过后,如果没有收敛,第二轮就只针对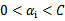 的样例进行迭代更新。
的样例进行迭代更新。
在第一个乘子选择后,第二个乘子也使用启发式方法选择,第二个乘子的迭代步长大致正比于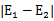 ,选择第二个乘子能够最大化
,选择第二个乘子能够最大化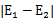 。即当
。即当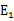 为正时选择负的绝对值最大的
为正时选择负的绝对值最大的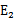 ,反之,选择正值最大的
,反之,选择正值最大的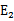 。
。
最后的收敛条件是在界内(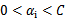 )的样例都能够遵循KKT条件,且其对应的
)的样例都能够遵循KKT条件,且其对应的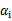 只在极小的范围内变动。
只在极小的范围内变动。
至于如何写具体的程序,请参考John C. Platt在论文中给出的伪代码。
13 总结
这份SVM的讲义重点概括了SVM的基本概念和基本推导,中规中矩却又让人醍醐灌顶。起初让我最头疼的是拉格朗日对偶和SMO,后来逐渐明白拉格朗日对偶的重要作用是将w的计算提前并消除w,使得优化函数变为拉格朗日乘子的单一参数优化问题。而SMO里面迭代公式的推导也着实让我花费了不少时间。
对比这么复杂的推导过程,SVM的思想确实那么简单。它不再像logistic回归一样企图去拟合样本点(中间加了一层sigmoid函数变换),而是就在样本中去找分隔线,为了评判哪条分界线更好,引入了几何间隔最大化的目标。
之后所有的推导都是去解决目标函数的最优化上了。在解决最优化的过程中,发现了w可以由特征向量内积来表示,进而发现了核函数,仅需要调整核函数就可以将特征进行低维到高维的变换,在低维上进行计算,实质结果表现在高维上。由于并不是所有的样本都可分,为了保证SVM的通用性,进行了软间隔的处理,导致的结果就是将优化问题变得更加复杂,然而惊奇的是松弛变量没有出现在最后的目标函数中。最后的优化求解问题,也被拉格朗日对偶和SMO算法化解,使SVM趋向于完美。
另外,其他很多议题如SVM背后的学习理论、参数选择问题、二值分类到多值分类等等还没有涉及到,以后有时间再学吧。其实朴素贝叶斯在分类二值分类问题时,如果使用对数比,那么也算作线性分类器。
SVM之SMO最小序列的更多相关文章
- SVM之SMO算法(转)
支持向量机(Support Vector Machine)-----SVM之SMO算法(转) 此文转自两篇博文 有修改 序列最小优化算法(英语:Sequential minimal optimizat ...
- Sequential Minimal Optimization(SMO,序列最小优化算法)初探
什么是SVM SVM是Support Vector Machine(支持向量机)的英文缩写,是上世纪九十年代兴起的一种机器学习算法,在目前神经网络大行其道的情况下依然保持着生命力.有人说现在是神经网络 ...
- 支持向量机(Support Vector Machine)-----SVM之SMO算法(转)
此文转自两篇博文 有修改 序列最小优化算法(英语:Sequential minimal optimization, SMO)是一种用于解决支持向量机训练过程中所产生优化问题的算法.SMO由微软研究院的 ...
- 详解svm和smo的出现
SupportVector Machines are learning models used forclassification: which individuals in a population ...
- ML-求解 SVM 的SMO 算法
这算是我真正意义上认真去读的第一篇ML论文了, but, 我还是很多地方没有搞懂, 想想, 缓缓吧, 还是先熟练调用API 哈哈 原论文地址: https://www.microsoft.com/en ...
- 机器学习实战 - 读书笔记(06) – SVM支持向量机
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习笔记,这次是第6章:SVM 支持向量机. 支持向量机不是很好被理解,主要是因为里面涉及到了许多数学知 ...
- SVM原理以及Tensorflow 实现SVM分类(附代码)
1.1. SVM介绍 1.2. 工作原理 1.2.1. 几何间隔和函数间隔 1.2.2. 最大化间隔 - 1.2.2.0.0.1. \(L( {x}^*)\)对$ {x}^*$求导为0 - 1.2.2 ...
- [笔记]关于支持向量机(SVM)中 SMO算法的学习(一)理论总结
1. 前言 最近又重新复习了一遍支持向量机(SVM).其实个人感觉SVM整体可以分成三个部分: 1. SVM理论本身:包括最大间隔超平面(Maximum Margin Classifier),拉格朗日 ...
- 支持向量机(SVM)中的 SMO算法
1. 前言 最近又重新复习了一遍支持向量机(SVM).其实个人感觉SVM整体可以分成三个部分: 1. SVM理论本身:包括最大间隔超平面(Maximum Margin Classifier),拉格朗日 ...
随机推荐
- 学习JQ
目前我对jq的了解还很少,只知道jq比js简单很多,只需引入一个js文件,然后,在js中很多行才能实现的代码,jq中或许一行就搞掂了,比如根据类名获取元素,$(".类名")即可,对 ...
- 51nod 1183 编辑距离(dp)
题目链接:51nod 1183 编辑距离 #include<cstdio> #include<cstring> #include<algorithm> using ...
- 关于电脑安装多个版本JDK后使用时的切换
描述:刚到新公司,自己安装了jdk1.7和开发工具myeclipse10,但是由于公司项目的需要(具体原因不详细描述了),需要使用myeclipse6.5和jdk1.6.于是在切换jdk1.7和jdk ...
- 基于天天动听API开发在线音乐查询网站
预览图 源码下载 地址:https://github.com/bajdcc/dev/tree/master/ttpod 文件夹说明: App_Code,WCF服务 Script,离线下载的celery ...
- App压力测试整理
压力测试结果:CRASH:崩溃,应用程序在使用过程中,非正常退出ANR:Application Not Responding MonkeyRunner APIs MonkeyRunner:用来连接设备 ...
- shell使用随笔
001 对文件某一列求和 awk '{sum += $collum};END {print sum}' /path/to/your/file 2 3 3 5 假设文件内容如上所示: # awk '{s ...
- 使用WinINet和WinHTTP实现Http访问
使用WinINet和WinHTTP实现Http访问 Http访问有两种方式,GET和POST,就编程来说GET方式相对简单点,它不用向服务器提交数据,在这个例程中我使用POST方式,提交数据value ...
- MONGODB 与sql聚合操作对应图
MongoDB 高级查询条件操作符 2012-04-25 15:35:19| 分类: MongoDB | 标签:mongodb使用 mongodb查询 |举报|字号 订阅 http://blo ...
- [TD Cup 2014] TDL的YC牌 & TDL的幼儿园
TDL的YC牌 传说中的置换群?反正不懂.我的思路竟然是对的,可是为何只有20分? (1)尼玛每行数据输出后回车不打! (2)写gcd函数脑残把a mod b写成a-b,大大减慢速度… (3)看标程才 ...
- Mybatis根据表自动生成相关代码
这个地方的生成需要用到三个文件,generatorConfig.xml.mybatis-generator-core-1.3.1.jar和mysql-connector-java-5.1.29.jar ...
