「PKUSC2018」神仙的游戏

题目链接

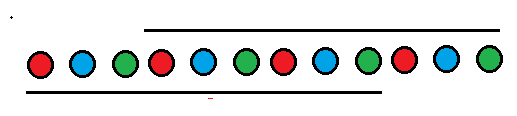
比如说上面\(|S|\)为12的字符串，我们欲求出\(f(9)\)的值，那么上面相同颜色的字符必须两两能够匹配。也就是说，同种颜色的字符集里不能同时出现0和1。如果只考虑同种颜色集里相邻的两个字符能否匹配，那么小样例都过不了。。

我们仔细观察就会发现，每隔\(|S|-len\)的位置就会出现相同的字符。我们可以认为长度为\(len\)的border实质上就是将长度为\(len\)的前缀向后偏移\(|S|-len\)，看是否能匹配。

如果有两个字符\(s[i],s[j]\ (i<j)\)，他们一个是0，一个是1，那么偏移量就不能为\(j-i\)。于是我们定义一个数组\(illegal\)。\(illegal[i]\)为1表示偏移量为\(i\)时不合法。

假设我们已经求出了\(illegal\)数组，我们判断\(f(len)\)的值，那么我们只需判断\(illegal[|S|-len]\)就可以了吗？当然不行，因为我们说了是字符集中不同时出现0和1，只判断\(illegal[|S|-len]\)相当于只判断了相邻两个字符能否匹配。所以我们还要判断\(|S|-len\)的倍数。

至于求\(illegal\)，就是经典的\(FFT/NTT\)在字符串匹配中的引用。可以构造一个反串，然后正反串做\(NTT\)就可以了。具体可以参考【BZOJ4259】残缺的字符串。

不过似乎不用这么麻烦，就直接将正串的1设为1，反串的0设为1然后一边\(NTT\)就行了。。

代码：

#include<bits/stdc++.h>
#define ll long long
#define N 500005
#define Z complex<double>
#define pi acos(-1)
#define mod 998244353

using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}

char s[N];
int rev[N<<2],n;
ll f[N<<2],g[N<<2];
ll Match[N<<2];

ll ksm(ll t,ll x) {
	ll ans=1;
	for(;x;x>>=1,t=t*t%mod)
		if(x&1) ans=ans*t%mod;
	return ans;
}
void NTT(ll *a,int d,int flag) {
	static const ll G=3;
	int n=1<<d;
	for(int i=0;i<n;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<d-1);
	for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
	for(int s=1;s<=d;s++) {
		int len=1<<s,mid=len>>1;
		ll w=flag==1?ksm(G,(mod-1)/len):ksm(G,mod-1-(mod-1)/len);
		for(int i=0;i<n;i+=len) {
			ll t=1;
			for(int j=0;j<mid;j++,t=t*w%mod) {
				ll u=a[i+j],v=a[i+j+mid]*t%mod;
				a[i+j]=(u+v)%mod;
				a[i+j+mid]=(u-v+mod)%mod;
			}
		}
	}
	if(flag==-1) {
		ll inv=ksm(n,mod-2);
		for(int i=0;i<n;i++) a[i]=a[i]*inv%mod;
	}
}
bool illegal[N<<2];
ll ans;
int main() {
	scanf("%s",s+1);
	n=strlen(s+1);
	int d=ceil(log2(n*2+2));

	for(int i=1;i<=n;i++) {
		if(s[i]=='?') f[i]=g[n+1-i]=0;
		else if(s[i]=='0') {
			f[i]=g[n+1-i]=1;
		} else {
			f[i]=8,g[n+1-i]=2;
		}
	}

	NTT(f,d,1),NTT(g,d,1);
	for(int i=0;i<(1<<d);i++) f[i]*=g[i];
	NTT(f,d,-1);

	for(int i=0;i<(1<<d);i++) Match[i]+=f[i];
	memset(f,0,sizeof(f));
	memset(g,0,sizeof(g));
	for(int i=1;i<=n;i++) {
		if(s[i]=='?') f[i]=g[n+1-i]=0;
		else if(s[i]=='0') {
			f[i]=g[n+1-i]=1;
		} else {
			f[i]=4,g[n+1-i]=4;
		}
	}
	NTT(f,d,1),NTT(g,d,1);
	for(int i=0;i<(1<<d);i++) f[i]*=g[i];
	NTT(f,d,-1);
	for(int i=0;i<(1<<d);i++) Match[i]-=2*f[i];
	memset(f,0,sizeof(f));
	memset(g,0,sizeof(g));
	for(int i=1;i<=n;i++) {
		if(s[i]=='?') f[i]=g[n+1-i]=0;
		else if(s[i]=='0') {
			f[i]=g[n+1-i]=1;
		} else {
			f[i]=2,g[n+1-i]=8;
		}
	}
	NTT(f,d,1),NTT(g,d,1);
	for(int i=0;i<(1<<d);i++) f[i]*=g[i];
	NTT(f,d,-1);
	for(int i=0;i<(1<<d);i++) Match[i]+=f[i];

	for(int i=0;i<=n+1;i++)
		if(Match[i]) illegal[abs(i-n-1)]=1;
	for(int i=1;i<=n;i++) {
		int flag=0;
		for(int j=i;j<=n;j+=i) {
			if(illegal[j]) {
				flag=1;
				break;
			}
		}
		if(!flag) ans^=1ll*(n-i)*(n-i);
	}
	ans^=1ll*n*n;
	cout<<ans;
	return 0;
}