PAT A1018 Public Bike Management （30 分）——最小路径，溯源，二标尺，DFS

There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

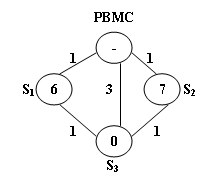
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S​3​​, we have 2 different shortest paths:

1. PBMC -> S​1​​ -> S​3​​. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S​1​​ and then take 5 bikes to S​3​​, so that both stations will be in perfect conditions.

2. PBMC -> S​2​​ -> S​3​​. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

Input Specification:

Each input file contains one test case. For each case, the first line contains 4 numbers: C​max​​ (≤100), always an even number, is the maximum capacity of each station; N (≤500), the total number of stations; S​p​​, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C​i​​ (i=1,⋯,N) where each C​i​​ is the current number of bikes at S​i​​ respectively. Then M lines follow, each contains 3 numbers: S​i​​, S​j​​, and T​ij​​ which describe the time T​ij​​ taken to move betwen stations S​i​​ and S​j​​. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0−>S​1​​−>⋯−>S​p​​. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of S​p​​ is adjusted to perfect.

Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge's data guarantee that such a path is unique.

Sample Input:

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1

Sample Output:

3 0->2->3 0

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <queue>
#include <string>
#include <set>
#include <map>
using namespace std;
const int maxn = , inf = ;
int cmax, n, sp, m;
int g[maxn][maxn], c[maxn] = {  };
vector<int> pre[maxn];
int d[maxn];
bool vis[maxn];
void dijkstra(int s) {
    fill(vis, vis + maxn, false);
    fill(d, d + maxn, inf);
    d[s] = ;
    for (int i = ; i <= n; i++) {
        int u = -, min = inf;
        for (int j = ; j < n; j++) {
            if (vis[j] == false && d[j] < min) {
                min = d[j];
                u = j;
            }
        }
        if (u == -) return;
        vis[u] = true;
        for (int v = ; v <= n; v++) {
            if (vis[v] == false && g[u][v]!=inf) {
                if (d[v] > d[u] + g[u][v]) {
                    d[v] = d[u] + g[u][v];
                    pre[v].clear();
                    pre[v].push_back(u);
                }
                else if (d[v] == d[u] + g[u][v]) {
                    pre[v].push_back(u);
                }
            }
        }
    }
}
vector<int> shortpath, temppath;
int min_c = inf, min_t = inf;
void dfs(int v) {
    if (v == ) {
        temppath.push_back(v);
        int s;
        int carry = , take = ;
        for (int i = temppath.size() - ; i >= ;i--) {
            s = temppath[i];
            if (cmax /  < c[s]) {
                take += c[s] - (cmax / );
            }
            else {
                carry = carry + max(, cmax /  - c[s] - take);
                take = max(, take - (cmax /  - c[s]));
            }
        }
        if (carry < min_c || (carry==min_c && take<min_t)) {
            min_c = carry;
            shortpath = temppath;
            min_t = take;
        }
        temppath.pop_back();
        return;
    }
    temppath.push_back(v);
    for (int i = ; i < pre[v].size(); i++) {
        dfs(pre[v][i]);
    }
    temppath.pop_back();
}
int main() {
    cin >> cmax >> n >> sp >> m;
    for (int i = ; i <= n; i++) {
        scanf("%d", &c[i]);
    }
    fill(g[], g[] + maxn * maxn, inf);
    for (int i = ; i < m; i++) {
        int c1, c2, w;
        scanf("%d %d %d", &c1, &c2, &w);
        g[c1][c2] = w;
        g[c2][c1] = w;
    }
    dijkstra();
    dfs(sp);
    printf("%d ", min_c);
    for (int i = shortpath.size() - ; i > ; i--) {
        printf("%d->", shortpath[i]);
    }
    printf("%d %d\n",shortpath[], min_t);

    system("pause");
    return ;
}

注意点：还是一道逻辑看似简单的题，考察一个多尺度最短路径。知道用dijkstra+dfs的方法最方便，就是死不相信想只用dijkstra做出来，发现真的不行，当带的车一样多时，最后带回来的车要最少，这个光用dijkstra是算不出来的，因为中间要尽可能多的带车出来，但最后要最少，如果中间带少的车出来，最后需要带的车又会太多。还是老老实实用dijkstra+dfs最方便。一定要把这个模板记住熟练了！