LCA树链剖分

LCA(Lowest Common Ancestor 最近公共祖先)定义如下：在一棵树中两个节点的LCA为这两个节点所有的公共祖先中深度最大的节点。

比如这棵树

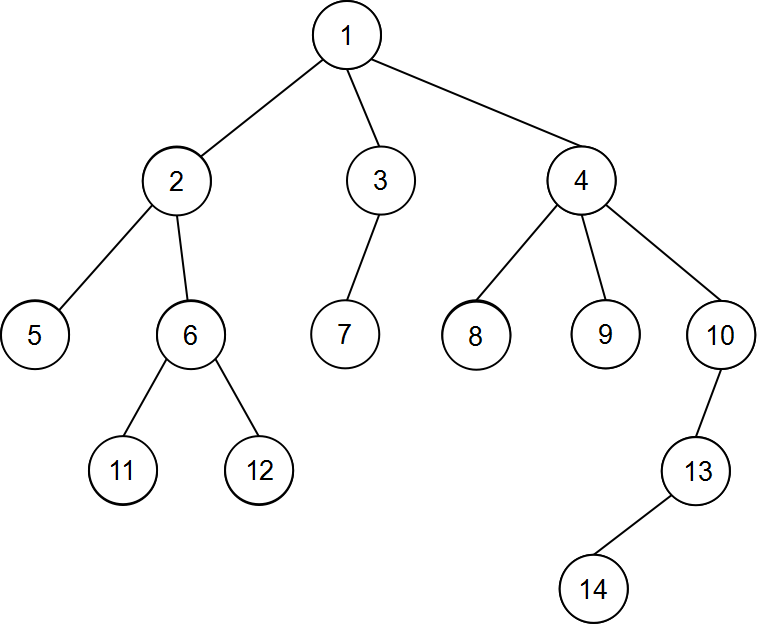
结点5和6的LCA是2,12和7的LCA是1,8和14的LCA是4。

这里讲一下用树链剖分来求LCA。

先想一下，若要求结点13和4的LCA，那很显然是4，因为他们在一条重链上。所谓的重链，就是取每个结点u的所有子节点中，子树最大的子结点v，然后将边(u,v)作为重边，其余边作为轻边，重边构成的链就是重链。子树最大就是指该点所得孩子结点最多（这里要包括他自己）。

我们先找出所有的重链。

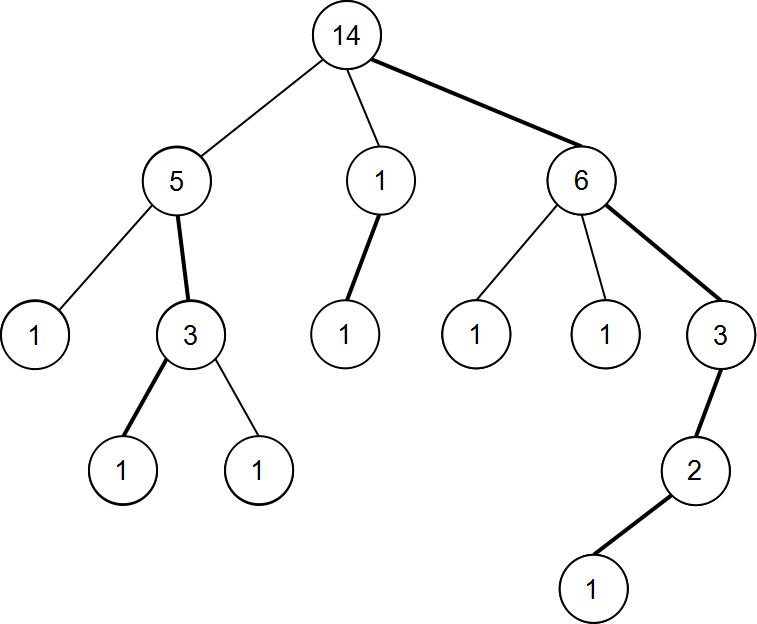
可见这棵树有7条重链（包括一条链只有一个结点的）。每一条重链的顶点就是该链上深度最小的结点。

而树链剖分的目标就是将要求的两个点转换到一条重链上，这样LCA就是该条重链上深度较小的结点了。

具体实现步骤拿第一幅图中的结点12和14举例。首先要比较的是12和14所在链的顶点的深度，可见12所在链的顶点更深，此时将12跳到它的顶点12的父亲结点6。然后再比较6所在链的顶点和14所在链的顶点，循环下去直到两个点到同一个链上，最后比较，收尾。

这就是树链剖分的基本思想了，那我就开始写了。

首先跑两遍dfs，第一遍是建树和建链，第二遍是记录每一个结点的顶点（这样就知道该点所在链的顶点的深度了）。然后就是用上述思想求LCA。

我们以洛谷的板子为例，传送门：https://www.luogu.org/problemnew/show/P3379

上代码（懒得用邻接表存图了，上vector）

其中vis数组是为了解决无向图存两次边的问题。

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<cstring>
 #include<vector>
 using namespace std;
 const int maxn = 5e5 + ;
 vector<int>v[maxn];
 /*第一遍dfs主要来维护以下这些数组，size[now]指结点now的子树大小，dep[now]指结点now的深度，
 Maxson[now]指now所在链上结点now的下一个结点（用来建链） */
 int vis[maxn], size[maxn], dep[maxn], fa[maxn], Maxson[maxn];
 void dfs1(int now)
 {
     vis[now] = ; size[now]= ;
     for(int i = ; i < v[now].size(); ++i)
         if(!vis[v[now][i]])
         {
             dep[v[now][i]] = dep[now] + ;
             fa[v[now][i]] = now;
             dfs1(v[now][i]);
             size[now] += size[v[now][i]];    //结点now的子树大小就是他所有孩子结点的大小之和加1（包括自己）
             if(size[v[now][i]] > size[Maxson[now]]) Maxson[now] = v[now][i];    //选重边
         }
 }
 int path[maxn];
 void dfs2(int now)
 {
     vis[now] = ;
     for(int i = ; i < v[now].size(); ++i)
         if(!vis[v[now][i]])
         {
             if(Maxson[now] == v[now][i]) path[v[now][i]] = path[now];
             else path[v[now][i]] = v[now][i];    //新开辟一条链
             dfs2(v[now][i]);
         }
 }
 int lca(int x, int y)
 {
     while(path[x] != path[y])    //若不在一条链上
     {
         if(dep[path[x]] > dep[path[y]]) x = fa[path[x]];
         else y = fa[path[y]];
     }
     return dep[x] < dep[y] ? x : y;
 }
 int main()
 {
     int n, m, s; scanf("%d%d%d", &n, &m, &s);
     for(int i = ; i < n; ++i)
     {
         int a, b; scanf("%d%d", &a, &b);
         v[a].push_back(b); v[b].push_back(a);
     }
     dep[s] = ; memset(vis, , sizeof(vis));
     dfs1(s);
     path[s] = s; memset(vis, , sizeof(vis));
     dfs2(s);
     for(int i = ; i <= m; ++i)
     {
         int a, b; scanf("%d%d", &a, &b);
         printf("%d\n", lca(a, b));
     }
     return ;
 }

我们再来分析一下时间复杂度：任意一个结点到根的路径，每遇到一条轻边，子树大小就至少翻一倍，所以最坏情况下是O(logn)，很牛吧？

洛谷的这个毒瘤板子题，我以前用RMQ和树上倍增写都会T两个点，加快读快输开氧气勉强过了，但是很不爽。直到有一天我会了树剖后，竟然直接AC，贼激动。

那我就讲到这了。啊对了，他有一个缺点，难写（还是RMQ简单）