一、关于聚类及相似度、距离的知识点

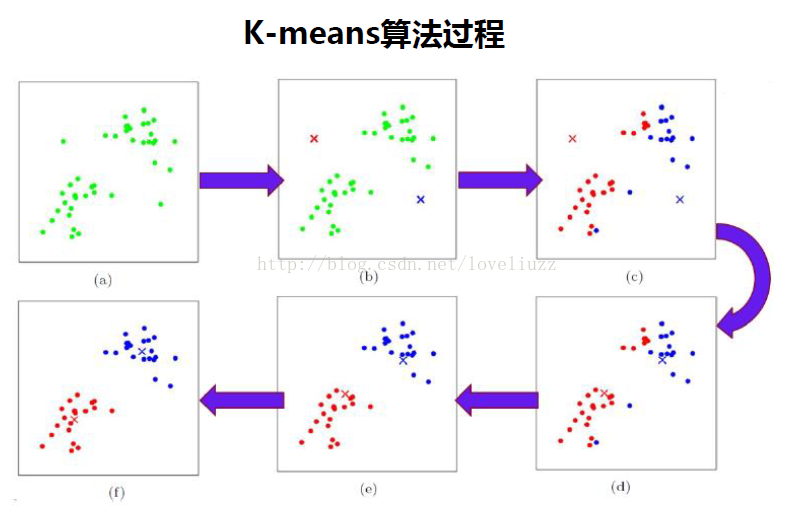
二、k-means算法思想与流程

三、sklearn中对于kmeans算法的参数

四、代码示例以及应用的知识点简介

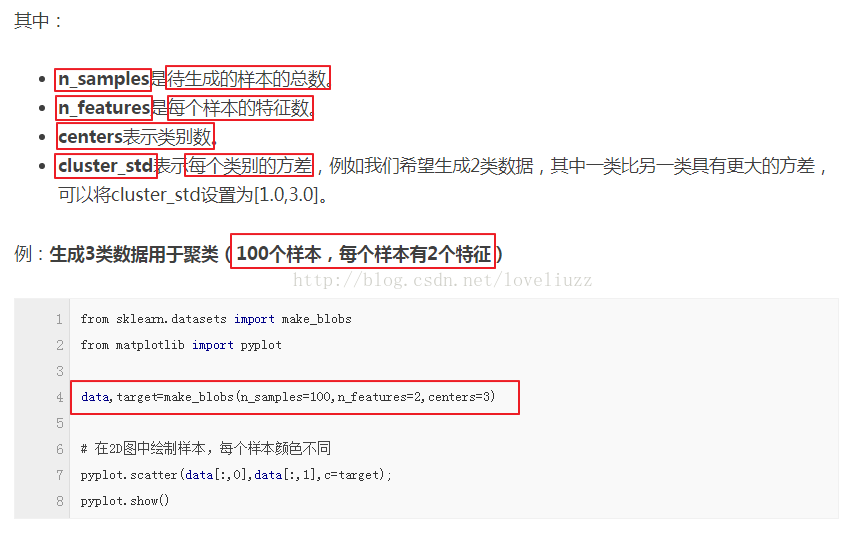
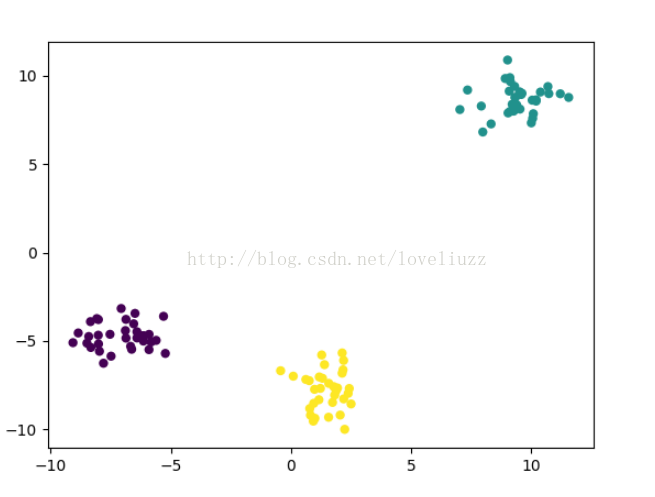
（1）make_blobs：聚类数据生成器

sklearn.datasets.make_blobs(n_samples=100, n_features=2,centers=3, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None)[source]

返回值为：

（2）np.vstack方法作用——堆叠数组

详细介绍参照博客链接：http://blog.csdn.net/csdn15698845876/article/details/73380803

  1. #!/usr/bin/env python
  2. # -*- coding:utf-8 -*-
  3. # Author:ZhengzhengLiu
  4. #k-means聚类算法
  5. import numpy as np
  6. import pandas as pd
  7. import matplotlib as mpl
  8. import matplotlib.pyplot as plt
  9. import matplotlib.colors
  10. import sklearn.datasets as ds
  11. from sklearn.cluster import KMeans      #引入kmeans
  12. #解决中文显示问题
  13. mpl.rcParams['font.sans-serif'] = [u'SimHei']
  14. mpl.rcParams['axes.unicode_minus'] = False
  15. #产生模拟数据
  16. N = 1500
  17. centers = 4
  18. #make_blobs:聚类数据生成器
  19. data,y = ds.make_blobs(N,n_features=2,centers=centers,random_state=28)
  20. data2,y2 = ds.make_blobs(N,n_features=2,centers=centers,random_state=28)
  21. data3 = np.vstack((data[y==0][:200],data[y==1][:100],data[y==2][:10],data[y==3][:50]))
  22. y3 = np.array([0]*200+[1]*100+[2]*10+[3]*50)
  23. #模型的构建
  24. km = KMeans(n_clusters=centers,random_state=28)
  25. km.fit(data,y)
  26. y_hat = km.predict(data)
  27. print("所有样本距离聚簇中心点的总距离和:",km.inertia_)
  28. print("距离聚簇中心点的平均距离:",(km.inertia_/N))
  29. print("聚簇中心点:",km.cluster_centers_)
  30. y_hat2 = km.fit_predict(data2)
  31. y_hat3 = km.fit_predict(data3)
  32. def expandBorder(a, b):
  33. d = (b - a) * 0.1
  34. return a-d, b+d
  35. #画图
  36. cm = mpl.colors.ListedColormap(list("rgbmyc"))
  37. plt.figure(figsize=(15,9),facecolor="w")
  38. plt.subplot(241)
  39. plt.scatter(data[:,0],data[:,1],c=y,s=30,cmap=cm,edgecolors="none")
  40. x1_min,x2_min = np.min(data,axis=0)
  41. x1_max,x2_max = np.max(data,axis=0)
  42. x1_min,x1_max = expandBorder(x1_min,x1_max)
  43. x2_min,x2_max = expandBorder(x2_min,x2_max)
  44. plt.xlim((x1_min,x1_max))
  45. plt.ylim((x2_min,x2_max))
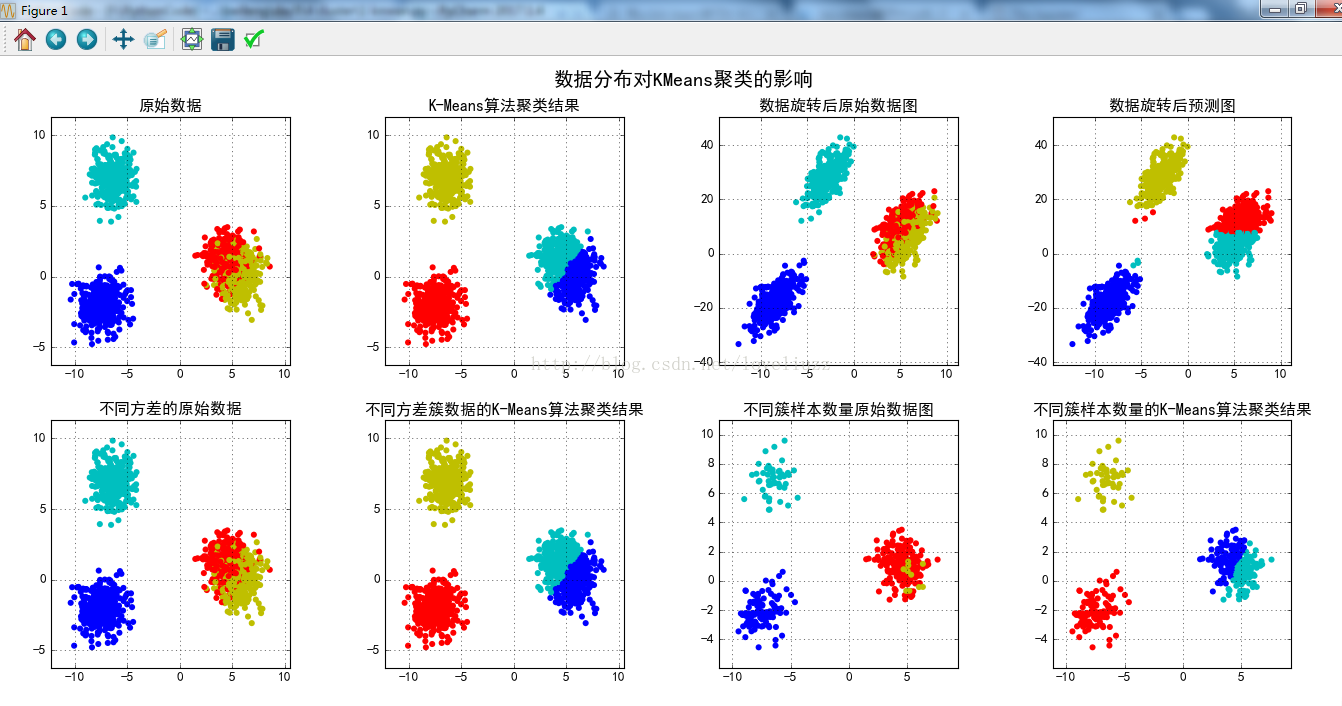
  46. plt.title("原始数据")
  47. plt.grid(True)
  48. plt.subplot(242)
  49. plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none')
  50. plt.xlim((x1_min, x1_max))
  51. plt.ylim((x2_min, x2_max))
  52. plt.title(u'K-Means算法聚类结果')
  53. plt.grid(True)
  54. m = np.array(((1, 1), (0.5, 5)))
  55. data_r = data.dot(m)
  56. y_r_hat = km.fit_predict(data_r)
  57. plt.subplot(243)
  58. plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
  59. x1_min, x2_min = np.min(data_r, axis=0)
  60. x1_max, x2_max = np.max(data_r, axis=0)
  61. x1_min, x1_max = expandBorder(x1_min, x1_max)
  62. x2_min, x2_max = expandBorder(x2_min, x2_max)
  63. plt.xlim((x1_min, x1_max))
  64. plt.ylim((x2_min, x2_max))
  65. plt.title(u'数据旋转后原始数据图')
  66. plt.grid(True)
  67. plt.subplot(244)
  68. plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none')
  69. plt.xlim((x1_min, x1_max))
  70. plt.ylim((x2_min, x2_max))
  71. plt.title(u'数据旋转后预测图')
  72. plt.grid(True)
  73. plt.subplot(245)
  74. plt.scatter(data2[:, 0], data2[:, 1], c=y2, s=30, cmap=cm, edgecolors='none')
  75. x1_min, x2_min = np.min(data2, axis=0)
  76. x1_max, x2_max = np.max(data2, axis=0)
  77. x1_min, x1_max = expandBorder(x1_min, x1_max)
  78. x2_min, x2_max = expandBorder(x2_min, x2_max)
  79. plt.xlim((x1_min, x1_max))
  80. plt.ylim((x2_min, x2_max))
  81. plt.title(u'不同方差的原始数据')
  82. plt.grid(True)
  83. plt.subplot(246)
  84. plt.scatter(data2[:, 0], data2[:, 1], c=y_hat2, s=30, cmap=cm, edgecolors='none')
  85. plt.xlim((x1_min, x1_max))
  86. plt.ylim((x2_min, x2_max))
  87. plt.title(u'不同方差簇数据的K-Means算法聚类结果')
  88. plt.grid(True)
  89. plt.subplot(247)
  90. plt.scatter(data3[:, 0], data3[:, 1], c=y3, s=30, cmap=cm, edgecolors='none')
  91. x1_min, x2_min = np.min(data3, axis=0)
  92. x1_max, x2_max = np.max(data3, axis=0)
  93. x1_min, x1_max = expandBorder(x1_min, x1_max)
  94. x2_min, x2_max = expandBorder(x2_min, x2_max)
  95. plt.xlim((x1_min, x1_max))
  96. plt.ylim((x2_min, x2_max))
  97. plt.title(u'不同簇样本数量原始数据图')
  98. plt.grid(True)
  99. plt.subplot(248)
  100. plt.scatter(data3[:, 0], data3[:, 1], c=y_hat3, s=30, cmap=cm, edgecolors='none')
  101. plt.xlim((x1_min, x1_max))
  102. plt.ylim((x2_min, x2_max))
  103. plt.title(u'不同簇样本数量的K-Means算法聚类结果')
  104. plt.grid(True)
  105. plt.tight_layout(2, rect=(0, 0, 1, 0.97))
  106. plt.suptitle(u'数据分布对KMeans聚类的影响', fontsize=18)
  107. plt.savefig("k-means聚类算法.png")
  108. plt.show()
  109. #运行结果：
  110. 所有样本距离聚簇中心点的总距离和: 2592.9990199
  111. 距离聚簇中心点的平均距离: 1.72866601327
  112. 聚簇中心点: [[ -7.44342199e+00  -2.00152176e+00]
  113. [  5.80338598e+00   2.75272962e-03]
  114. [ -6.36176159e+00   6.94997331e+00]
  115. [  4.34372837e+00   1.33977807e+00]]

代码中用到的知识点：

  1. #!/usr/bin/env python
  2. # -*- coding:utf-8 -*-
  3. # Author:ZhengzhengLiu
  4. #kmean与mini batch kmeans 算法的比较
  5. import time
  6. import numpy as np
  7. import matplotlib as mpl
  8. import matplotlib.pyplot as plt
  9. import matplotlib.colors
  10. from sklearn.cluster import KMeans,MiniBatchKMeans
  11. from sklearn.datasets.samples_generator import make_blobs
  12. from sklearn.metrics.pairwise import pairwise_distances_argmin
  13. #解决中文显示问题
  14. mpl.rcParams['font.sans-serif'] = [u'SimHei']
  15. mpl.rcParams['axes.unicode_minus'] = False
  16. #初始化三个中心
  17. centers = [[1,1],[-1,-1],[1,-1]]
  18. clusters = len(centers)     #聚类数目为3
  19. #产生3000组二维数据样本，三个中心点，标准差是0.7
  20. X,Y = make_blobs(n_samples=300,centers=centers,cluster_std=0.7,random_state=28)
  21. #构建kmeans算法
  22. k_means =  KMeans(init="k-means++",n_clusters=clusters,random_state=28)
  23. t0 = time.time()
  24. k_means.fit(X)      #模型训练
  25. km_batch = time.time()-t0       #使用kmeans训练数据消耗的时间
  26. print("K-Means算法模型训练消耗时间:%.4fs"%km_batch)
  27. #构建mini batch kmeans算法
  28. batch_size = 100        #采样集的大小
  29. mbk = MiniBatchKMeans(init="k-means++",n_clusters=clusters,batch_size=batch_size,random_state=28)
  30. t0 = time.time()
  31. mbk.fit(X)
  32. mbk_batch = time.time()-t0
  33. print("Mini Batch K-Means算法模型训练消耗时间:%.4fs"%mbk_batch)
  34. #预测结果
  35. km_y_hat = k_means.predict(X)
  36. mbk_y_hat = mbk.predict(X)
  37. #获取聚类中心点并对其排序
  38. k_means_cluster_center = k_means.cluster_centers_
  39. mbk_cluster_center = mbk.cluster_centers_
  40. print("K-Means算法聚类中心点:\n center=",k_means_cluster_center)
  41. print("Mini Batch K-Means算法聚类中心点:\n center=",mbk_cluster_center)
  42. order = pairwise_distances_argmin(k_means_cluster_center,mbk_cluster_center)
  43. #画图
  44. plt.figure(figsize=(12,6),facecolor="w")
  45. plt.subplots_adjust(left=0.05,right=0.95,bottom=0.05,top=0.9)
  46. cm = mpl.colors.ListedColormap(['#FFC2CC', '#C2FFCC', '#CCC2FF'])
  47. cm2 = mpl.colors.ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
  48. #子图1——原始数据
  49. plt.subplot(221)
  50. plt.scatter(X[:,0],X[:,1],c=Y,s=6,cmap=cm,edgecolors="none")
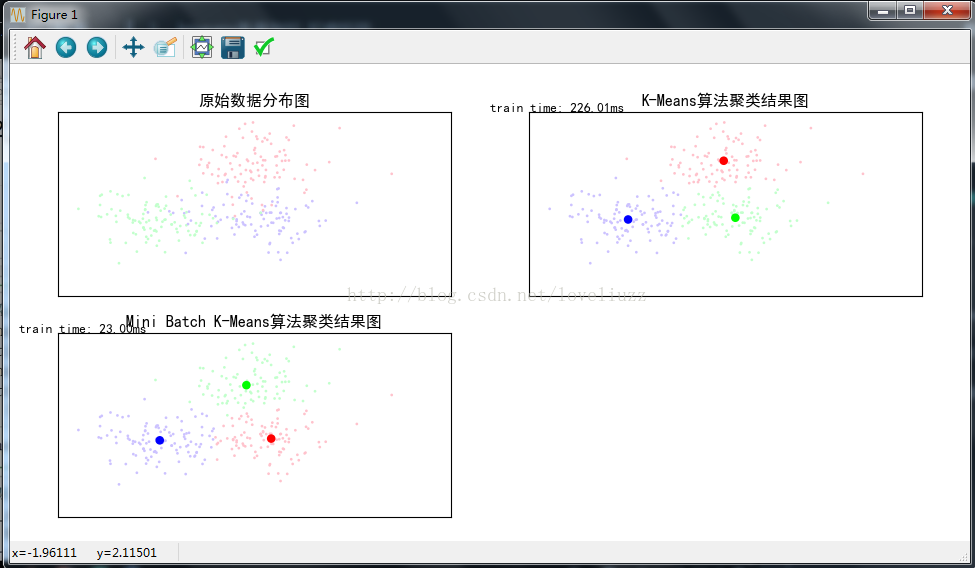
  51. plt.title(u"原始数据分布图")
  52. plt.xticks(())
  53. plt.yticks(())
  54. plt.grid(True)
  55. #子图2：K-Means算法聚类结果图
  56. plt.subplot(222)
  57. plt.scatter(X[:,0], X[:,1], c=km_y_hat, s=6, cmap=cm,edgecolors='none')
  58. plt.scatter(k_means_cluster_center[:,0], k_means_cluster_center[:,1],c=range(clusters),s=60,cmap=cm2,edgecolors='none')
  59. plt.title(u'K-Means算法聚类结果图')
  60. plt.xticks(())
  61. plt.yticks(())
  62. plt.text(-3.8, 3,  'train time: %.2fms' % (km_batch*1000))
  63. plt.grid(True)
  64. #子图三Mini Batch K-Means算法聚类结果图
  65. plt.subplot(223)
  66. plt.scatter(X[:,0], X[:,1], c=mbk_y_hat, s=6, cmap=cm,edgecolors='none')
  67. plt.scatter(mbk_cluster_center[:,0], mbk_cluster_center[:,1],c=range(clusters),s=60,cmap=cm2,edgecolors='none')
  68. plt.title(u'Mini Batch K-Means算法聚类结果图')
  69. plt.xticks(())
  70. plt.yticks(())
  71. plt.text(-3.8, 3,  'train time: %.2fms' % (mbk_batch*1000))
  72. plt.grid(True)
  73. plt.savefig("kmean与mini batch kmeans 算法的比较.png")
  74. plt.show()
  75. #运行结果：
  76. K-Means算法模型训练消耗时间:0.2260s
  77. Mini Batch K-Means算法模型训练消耗时间:0.0230s
  78. K-Means算法聚类中心点:
  79. center= [[ 0.96091862  1.13741775]
  80. [ 1.1979318  -1.02783007]
  81. [-0.98673669 -1.09398768]]
  82. Mini Batch K-Means算法聚类中心点:
  83. center= [[ 1.34304199 -1.01641075]
  84. [ 0.83760683  1.01229021]
  85. [-0.92702179 -1.08205992]]

五、聚类算法的衡量指标

    1. #!/usr/bin/env python
    2. # -*- coding:utf-8 -*-
    3. # Author:ZhengzhengLiu
    4. #聚类算法评估
    5. import time
    6. import numpy as np
    7. import matplotlib as mpl
    8. import matplotlib.pyplot as plt
    9. import matplotlib.colors
    10. from sklearn.cluster import KMeans,MiniBatchKMeans
    11. from sklearn import metrics
    12. from sklearn.metrics.pairwise import pairwise_distances_argmin
    13. from sklearn.datasets.samples_generator import make_blobs
    14. #解决中文显示问题
    15. mpl.rcParams['font.sans-serif'] = [u'SimHei']
    16. mpl.rcParams['axes.unicode_minus'] = False
    17. #初始化三个中心
    18. centers = [[1,1],[-1,-1],[1,-1]]
    19. clusters = len(centers)     #聚类数目为3
    20. #产生3000组二维数据样本，三个中心点，标准差是0.7
    21. X,Y = make_blobs(n_samples=300,centers=centers,cluster_std=0.7,random_state=28)
    22. #构建kmeans算法
    23. k_means =  KMeans(init="k-means++",n_clusters=clusters,random_state=28)
    24. t0 = time.time()
    25. k_means.fit(X)      #模型训练
    26. km_batch = time.time()-t0       #使用kmeans训练数据消耗的时间
    27. print("K-Means算法模型训练消耗时间:%.4fs"%km_batch)
    28. #构建mini batch kmeans算法
    29. batch_size = 100        #采样集的大小
    30. mbk = MiniBatchKMeans(init="k-means++",n_clusters=clusters,batch_size=batch_size,random_state=28)
    31. t0 = time.time()
    32. mbk.fit(X)
    33. mbk_batch = time.time()-t0
    34. print("Mini Batch K-Means算法模型训练消耗时间:%.4fs"%mbk_batch)
    35. km_y_hat = k_means.labels_
    36. mbkm_y_hat = mbk.labels_
    37. k_means_cluster_centers = k_means.cluster_centers_
    38. mbk_means_cluster_centers = mbk.cluster_centers_
    39. print ("K-Means算法聚类中心点:\ncenter=", k_means_cluster_centers)
    40. print ("Mini Batch K-Means算法聚类中心点:\ncenter=", mbk_means_cluster_centers)
    41. order = pairwise_distances_argmin(k_means_cluster_centers,
    42. mbk_means_cluster_centers)
    43. #效果评估
    44. ### 效果评估
    45. score_funcs = [
    46. metrics.adjusted_rand_score,    #ARI（调整兰德指数）
    47. metrics.v_measure_score,        #均一性与完整性的加权平均
    48. metrics.adjusted_mutual_info_score, #AMI（调整互信息）
    49. metrics.mutual_info_score,      #互信息
    50. ]
    51. ## 2. 迭代对每个评估函数进行评估操作
    52. for score_func in score_funcs:
    53. t0 = time.time()
    54. km_scores = score_func(Y, km_y_hat)
    55. print("K-Means算法:%s评估函数计算结果值:%.5f；计算消耗时间:%0.3fs" % (score_func.__name__, km_scores, time.time() - t0))
    56. t0 = time.time()
    57. mbkm_scores = score_func(Y, mbkm_y_hat)
    58. print("Mini Batch K-Means算法:%s评估函数计算结果值:%.5f；计算消耗时间:%0.3fs\n" % (score_func.__name__, mbkm_scores, time.time() - t0))
    59. #运行结果：
    60. K-Means算法模型训练消耗时间:0.6350s
    61. Mini Batch K-Means算法模型训练消耗时间:0.0900s
    62. K-Means算法聚类中心点:
    63. center= [[ 0.96091862  1.13741775]
    64. [ 1.1979318  -1.02783007]
    65. [-0.98673669 -1.09398768]]
    66. Mini Batch K-Means算法聚类中心点:
    67. center= [[ 1.34304199 -1.01641075]
    68. [ 0.83760683  1.01229021]
    69. [-0.92702179 -1.08205992]]
    70. K-Means算法:adjusted_rand_score评估函数计算结果值:0.72566；计算消耗时间:0.071s
    71. Mini Batch K-Means算法:adjusted_rand_score评估函数计算结果值:0.69544；计算消耗时间:0.001s
    72. K-Means算法:v_measure_score评估函数计算结果值:0.67529；计算消耗时间:0.004s
    73. Mini Batch K-Means算法:v_measure_score评估函数计算结果值:0.65055；计算消耗时间:0.004s
    74. K-Means算法:adjusted_mutual_info_score评估函数计算结果值:0.67263；计算消耗时间:0.006s
    75. Mini Batch K-Means算法:adjusted_mutual_info_score评估函数计算结果值:0.64731；计算消耗时间:0.005s
    76. K-Means算法:mutual_info_score评估函数计算结果值:0.74116；计算消耗时间:0.002s
    77. Mini Batch K-Means算法:mutual_info_score评估函数计算结果值:0.71351；计算消耗时间:0.001s

机器学习sklearn19.0聚类算法——Kmeans算法的更多相关文章

  1. [聚类算法] K-means 算法

    聚类 和 k-means简单概括. 聚类是一种 无监督学习 问题,它的目标就是基于 相似度 将相似的子集聚合在一起. k-means算法是聚类分析中使用最广泛的算法之一.它把n个对象根据它们的属性分为 ...

  2. 数据聚类算法-K-means算法

    深入浅出K-Means算法 摘要: 在数据挖掘中,K-Means算法是一种 cluster analysis 的算法,其主要是来计算数据聚集的算法,主要通过不断地取离种子点最近均值的算法. K-Mea ...

  3. 机器学习--聚类系列--K-means算法

    一.聚类 聚类分析是非监督学习的很重要的领域.所谓非监督学习,就是数据是没有类别标记的,算法要从对原始数据的探索中提取出一定的规律.而聚类分析就是试图将数据集中的样本划分为若干个不相交的子集,每个子集 ...

  4. 【转】 聚类算法-Kmeans算法的简单实现

    1. 聚类与分类的区别: 首先要来了解的一个概念就是聚类,简单地说就是把相似的东西分到一组,同 Classification (分类)不同,对于一个 classifier ,通常需要你告诉它“这个东西 ...

  5. 吴恩达机器学习笔记（七） —— K-means算法

    主要内容: 一.K-means算法简介 二.算法过程 三.随机初始化 四.二分K-means 四.K的选择 一.K-means算法简介 1.K-means算法是一种无监督学习算法.所谓无监督式学习,就 ...

  6. 数据挖掘经典算法——K-means算法

    算法描述 K-means算法是一种被广泛使用的基于划分的聚类算法,目的是将n个对象会分成k个簇.算法的具体描述如下: 随机选取k个对象作为簇中心: Do 计算所有对象到这k个簇中心的距离,将距离最近的 ...

  7. 算法 - k-means算法

    一.聚类思想 所谓聚类算法是指将一堆没有标签的数据自动划分成几类的方法,属于无监督学习方法,这个方法要保证同一类的数据有相似的特征,如下图所示:     根据样本之间的距离或者说是相似性(亲疏性),把 ...

  8. GMM算法k-means算法的比较

    1.EM算法 GMM算法是EM算法族的一个具体例子. EM算法解决的问题是:要对数据进行聚类,假定数据服从杂合的几个概率分布,分布的具体参数未知,涉及到的随机变量有两组,其中一组可观测另一组不可观测. ...

  9. 数据挖掘算法——K-means算法

    k-means中文称为K均值聚类算法,在1967年就被提出  所谓聚类就是将物理或者抽象对象的集合分组成为由类似的对象组成的多个簇的过程 聚类生成的组成为簇 簇内部任意两个对象之间具有较高的相似度,不 ...

随机推荐

  1. .Net Core(三)MVC Core

    MVC Core的改动感觉挺大的,需要的功能大多从Nuget安装,还内置了IOC,支持SelfHost方式运行等等. 一.项目结构的变化创建的新MVC项目的结构发生了变化,比如:静态文件需要统一放置到 ...

  2. 微信小程序-01-项目组成文件介绍（入门篇）

    自古开篇先说两句,写这些笔记不是学习用的,主要是后续分享一些遇到的坑,碰到过什么样的问题,怎么去解决,如果你不是一个很耐心无看文章的人,建议去 网易云课堂找一些课程,跟着别人的脚步或许会更有动力,我的 ...

  3. JavaScript大杂烩0 - WEB基础知识

    1. 协议小结:HTTP协议与TCP/IP协议 现代Web应用开发的基础是HTTP协议,那么HTTP协议与我们熟知的TCP/IP协议有什么关系呢? 这个要从网络通信模型说起,简单的说,计算机通信就像两 ...

  4. maven(六)，外置maven运行环境配置

    外置maven eclipse内置的maven插件是固定版本,如果要用其他版本的maven,可以使用外置maven 下载地址: http://maven.apache.org/download.cgi ...

  5. js中var的有或无--重复声明和以后的声明

    js中var的有或无--重复声明和以后的声明 使用var语句多次声明一个变量不仅是合法的,而且也不会造成任何错误. 如果重复使用的一个声明有一个初始值,那么它担当的不过是一个赋值语句的角色. 如果重复 ...

  6. January 23rd, 2018 Week 04th Tuesday

    Remembrance is a form of meeting, forgetfulness is a form of freedom. 记忆是一种相遇,遗忘是一种自由. Cherish those ...

  7. Orcale日期函数to_date(),to_char()

    日期转换的两个函数分别是to_date()和to_char(),to_date() 作用将字符类型按一定格式转化为日期类型, to_char() 将日期转按一定格式换成字符类型 其中当时间需要精确的时 ...

  8. JAVA中实现单例(Singleton)模式的八种方式

    单例模式 单例模式,是一种常用的软件设计模式.在它的核心结构中只包含一个被称为单例的特殊类.通过单例模式可以保证系统中,应用该模式的类一个类只有一个实例.即一个类只有一个对象实例. 基本的实现思路 单 ...

  9. [经验总结] 在 windows 命令窗口中运行 python 脚本时提示 ModuleNotFoundError: No module named 'xxx'

    先给出的代码和目录结构 获取CPU代码如下: # -*- coding:utf-8 -*- ''' Created on Sep 10, 2018 @author: ''' import sys im ...

  10. 使用POI读写word docx文件

    目录 1     读docx文件 1.1     通过XWPFWordExtractor读 1.2     通过XWPFDocument读 2     写docx文件 2.1     直接通过XWPF ...