• 首先splay和treap不一样，treap通过随机数来调整树的形态。但splay不一样，再每插入或操作一次后，你都会把他旋转到根，再旋转过程中树的形态会不断改变，这样来达到均摊效果 常数据大。

  • 来看看具体实现吧

    首先定义数组，\(size\) 子树大小（包括自己），\(fa\) 节点的父亲，\(key\) 该节点的权值，\(cnt\) 该节点权值出现次数，$ch $表示儿子 0表左二子，1表右儿子

首先看几个简单函数

  1. inline void update(int x)
  2. {
  3. 	size[x]=cnt[x]+size[ch[x][0]]+size[ch[x][1]];
  4. }

更新子树大小

  1. inline int get(int x){return x==ch[fa[x]][1];}

返回该节点是left儿子还是right儿子

  1. inline void clear(int x){ch[x][0]=ch[x][1]=fa[x]=size[x]=cnt[x]=key[x]=0;}

删除该节点，清空所有信息

接下来是splay的精髓所在

  1. inline void rotate(int x,int &k)
  2. {
  3.     static int old,oldfa,o;
  4.     old=fa[x];oldfa=fa[old];o=get(x);
  5.     if(old==k)k=x;
  6.     else ch[oldfa][get(old)]=x;
  7.     fa[x]=oldfa;
  8.     ch[old][o]=ch[x][o^1];fa[ch[x][o^1]]=old;
  9.     ch[x][o^1]=old;fa[old]=x;
  10.     update(x),update(old);
  11. }
  12. inline void splay(int x,int &k)
  13. {
  14.     while(x!=k)
  15.     {
  16.         if(fa[x]!=k)rotate(get(x)^get(fa[x])?x:fa[x],k);
  17.         rotate(x,k);
  18.     }
  19. }

rotate，splay，是splay核心操作，显然splay是依赖于rotate的，让我们看一下rotate是如何实现的吧



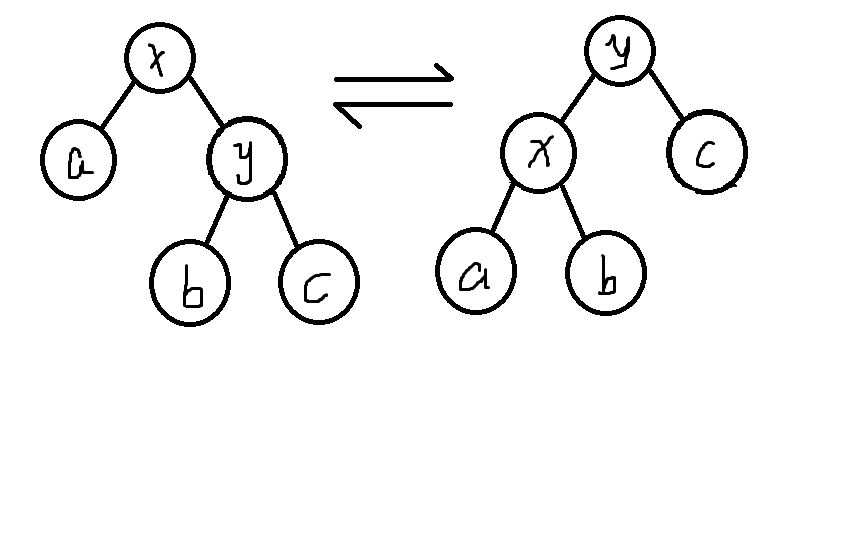
（手绘图）

我们考虑从图上左往右的过程，我们要将y旋上去，因为y本是x的右儿子，所以x放到y的左儿子，将y的原本左儿子设为x的右儿子，这是左旋，还有对称操作右旋，但我们不必要打两个函数，用 ^可以实现左右儿子的转换，用get操作实现，具体实现参考代码，打代码时最好画个图参照一下。

splay，这个操作完全依靠rotate，目的就是把你要的节点旋转到k（一般是root），k要传地址，要修改。在while循环里加了个小小的优化，但x和他的fa在同一侧时可以旋fa，以此来改变树的形态，(不怕被卡可以不写)

  1. inline void insert(int x)
  2. {
  3.     if(!root){root=++sz;size[sz]=cnt[sz]=1;key[sz]=x;return;}
  4.     int now=root,o;
  5.     while(1)
  6.     {
  7.         if(x==key[now])
  8.         {
  9.             ++cnt[now];
  10.             splay(now,root);
  11.             update(now);
  12. 			return;
  13.         }
  14.         o=x>key[now]?1:0;
  15.         if(!ch[now][o])
  16.         {
  17.             ch[now][o]=++sz;
  18.             size[sz]=cnt[sz]=1;
  19.             key[sz]=x;fa[sz]=now;
  20.             splay(sz,root);
  21.             return;
  22.         }
  23.         else now=ch[now][o];
  24.     }
  25. }

insert，插入一个数，当没有数时就直接把这个数设为根，else 因为树满足二叉排序树的性质，所以比当前节点的key小就往左走，否则往右走，直到找到一个空节点，更新信息，由于这个点以上所有的点\(size\)都要加一，不好update，所以把这给点旋转到根，将这个点update就行了

  1. inline int find_pos(int x)
  2. {
  3.     int now=root;
  4.     while(1)
  5.     {
  6.         if(x==key[now]){return now;}
  7.         if(x<key[now])now=ch[now][0];
  8.         else now=ch[now][1];
  9.     }
  10. }

找到该值在树中的节点编号

  1. inline int pre()
  2. {
  3.         int now=ch[root][0];
  4. 	while(ch[now][1])now=ch[now][1];
  5. 	return now;
  6. }
  7. inline int nex()
  8. {
  9.         int now=ch[root][1];
  10. 	while(ch[now][0])now=ch[now][0];
  11. 	return now;
  12. }

求前驱，后继，前驱从根的左儿子开始一直往右跑，后继从根的右儿子开始一直往左跑即可

  1. void del(int x)
  2. {
  3.     splay(find_pos(x),root);
  4.     if(cnt[root]>1){--cnt[root];return;}
  5.     if(!ch[root][0]&&!ch[root][1]){clear(root);root=0;return;}
  6.     if(ch[root][0]&&ch[root][1])
  7.     {
  8.         int oldroot=root;
  9.         splay(pre(),root);
  10.         fa[ch[oldroot][1]]=root;
  11.         ch[root][1]=ch[oldroot][1];
  12.         clear(oldroot);
  13.         update(root);
  14.     }
  15.     else
  16.     {
  17.         int o=ch[root][1]>0;
  18.         root=ch[root][o];
  19.         clear(fa[root]);
  20.         fa[root]=0;
  21.     }
  22. }

删除操作，有点麻烦，先找到x的位置

  • 如果x有多个就\(cnt\)减一
  • 如果一个儿子都没有就直接删掉，root设为0
  • 如果 只有一个儿子就把儿子设为根，删去这个点
  • 剩下两个儿子情况，找到根的前驱，把前驱旋到根，这是root只有左儿子，再把原来根的右儿子到root上，这样原来的root就脱离了树，再删掉即可。
  1. inline int find_order_of_key(int x)
  2. {
  3.     int res=0,now=root;
  4.     while(1)
  5.     {
  6.         if(x<key[now])now=ch[now][0];
  7.         else
  8.         {
  9.             res+=size[ch[now][0]];
  10.             if(x==key[now]){splay(now,root);return res+1;}
  11.             res+=cnt[now];
  12.             now=ch[now][1];
  13.         }
  14.     }
  15. }
  16. inline int find_by_order(int x)
  17. {
  18.     int now=root;
  19.     while(1)
  20.     {
  21.         if(x<=size[ch[now][0]])now=ch[now][0];
  22.         else
  23.         {
  24.             int temp=size[ch[now][0]]+cnt[now];
  25.             if(x<=temp)return key[now];
  26.             else{x-=temp;now=ch[now][1];}
  27.         }
  28.     }
  29. }

找x的排名，与找排名为x的数，其实大同小异，用二叉搜索树的性质即可，只是记得答案不一样罢了

  1. inline void rever(int x)
  2. {
  3.     swap(ch[x][0],ch[x][1]);
  4.     rev[ch[x][0]]^=1;rev[ch[x][1]]^=1;
  5.     rev[x]=0;
  6. }
  7. inline void rever(int l,int r)
  8. {
  9. 	l=find(l-1);r=find(r+1);
  10.         splay(l,root);splay(r,ch[l][1]);
  11.         rev[ch[r][0]]^=1;
  12. }

找到区间左边一个和区间的右边一个点在树中位置，把左边的点旋转到根，再把右边的点旋到root的右儿子，这时这段区间一定是ch[r][0]的子树（想一想，为什么）（根据二叉搜索树的性质），把这个点打上标记即可；当遇到有翻转标记的点时，交换其左右子树，并下传标记即可，注意，翻转操作只有可能在维护无序数列时使用，在有序数列中不需要也不能翻转，不然就无法满足排序二叉树的性质。

翻转操作在找节点的编号时才执行，详见下面代码

ok，splay的基本操作就是这些了

下面是完整代码

洛谷P3369 treap模板

题目描述

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

  1. 插入x数
  3. 删除x数(若有多个相同的数，因只删除一个)
  5. 查询x数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数，因输出最小的排名)
  7. 查询排名为x的数
  9. 求x的前驱(前驱定义为小于x，且最大的数)
  10. 求x的后继(后继定义为大于x，且最小的数)
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. typedef int sign;
  4. typedef long long ll;
  5. #define For(i,a,b) for(register sign i=(sign)a;i<=(sign)b;++i)
  6. #define Fordown(i,a,b) for(register sign i=(sign)a;i>=(sign)b;--i)
  7. const int N=1e5+5;
  8. void cmax(sign &a,sign b){if(a<b)a=b;}
  9. void cmin(sign &a,sign b){if(a>b)a=b;}
  10. template<typename T>T read()
  11. {
  12.     T ans=0,f=1;
  13.     char ch=getchar();
  14.     while(!isdigit(ch)&&ch!='-')ch=getchar();
  15.     if(ch=='-')f=-1,ch=getchar();
  16.     while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch-'0'),ch=getchar();
  17.     return ans*f;
  18. }
  19. void file()
  20. {
  21.     #ifndef ONLINE_JUDGE
  22.         freopen("splay.in","r",stdin);
  23.         freopen("splay.out","w",stdout);
  24.     #endif
  25. }
  26. int fa[N],size[N],key[N],cnt[N],ch[N][2],sz,root;
  27. inline void update(int x){size[x]=cnt[x]+size[ch[x][0]]+size[ch[x][1]];}
  28. inline int get(int x){return x==ch[fa[x]][1];}
  29. inline void clear(int x){ch[x][0]=ch[x][1]=fa[x]=size[x]=cnt[x]=key[x]=0;}
  30. inline void rotate(int x,int &k)
  31. {
  32.     static int old,oldfa,o;
  33.     old=fa[x];oldfa=fa[old];o=get(x);
  34.     if(old==k)k=x;
  35.     else ch[oldfa][get(old)]=x;
  36.     fa[x]=oldfa;
  37.     ch[old][o]=ch[x][o^1];fa[ch[x][o^1]]=old;
  38.     ch[x][o^1]=old;fa[old]=x;
  39.     update(x),update(old);
  40. }
  41. inline void splay(int x,int &k)
  42. {
  43.     while(x!=k)
  44.     {
  45.         if(fa[x]!=k)rotate(get(x)^get(fa[x])?x:fa[x],k);
  46.         rotate(x,k);
  47.     }
  48. }
  49. inline void insert(int x)
  50. {
  51.     //puts("");
  52.     if(!root){root=++sz;size[sz]=cnt[sz]=1;key[sz]=x;return;}
  53.     int now=root,o;
  54.     while(1)
  55.     {
  56.         if(x==key[now])
  57.         {
  58.             ++cnt[now];
  59.             splay(now,root);
  60.             update(now);
  61.             return;
  62.         }
  63.         o=x>key[now]?1:0;
  64.         if(!ch[now][o])
  65.         {
  66.             ch[now][o]=++sz;
  67.             size[sz]=cnt[sz]=1;
  68.             key[sz]=x;fa[sz]=now;
  69.             splay(sz,root);
  70.             return;
  71.         }
  72.         else now=ch[now][o];
  73.         //printf("%d %d %d %d\n",now,fa[now],ch[now][0],ch[now][1]);
  74.     }
  75. }
  76. inline int find_pos(int x)
  77. {
  78.     int now=root;
  79.     while(1)
  80.     {
  81.         if(x==key[now]){return now;}
  82.         if(x<key[now])now=ch[now][0];
  83.         else now=ch[now][1];
  84.     }
  85. }
  86. inline int pre()
  87. {
  88.     int now=ch[root][0];
  89.     while(ch[now][1])now=ch[now][1];
  90.     return now;
  91. }
  92. inline int nex()
  93. {
  94.     int now=ch[root][1];
  95.     while(ch[now][0])now=ch[now][0];
  96.     return now;
  97. }
  98. void del(int x)
  99. {
  100.     splay(find_pos(x),root);
  101.     if(cnt[root]>1){--cnt[root];return;}
  102.     if(!ch[root][0]&&!ch[root][1]){clear(root);root=0;return;}
  103.     if(ch[root][0]&&ch[root][1])
  104.     {
  105.         int oldroot=root;
  106.         splay(pre(),root);
  107.         fa[ch[oldroot][1]]=root;
  108.         ch[root][1]=ch[oldroot][1];
  109.         clear(oldroot);
  110.         update(root);
  111.     }
  112.     else
  113.     {
  114.         int o=ch[root][1]>0;
  115.         root=ch[root][o];
  116.         clear(fa[root]);
  117.         fa[root]=0;
  118.     }
  119. }
  120. inline int find_order_of_key(int x)
  121. {
  122.     int res=0,now=root;
  123.     while(1)
  124.     {
  125.         if(x<key[now])now=ch[now][0];
  126.         else
  127.         {
  128.             res+=size[ch[now][0]];
  129.             if(x==key[now]){splay(now,root);return res+1;}
  130.             res+=cnt[now];
  131.             now=ch[now][1];
  132.         }
  133.     }
  134. }
  135. inline int find_by_order(int x)
  136. {
  137.     int now=root;
  138.     while(1)
  139.     {
  140.         if(x<=size[ch[now][0]])now=ch[now][0];
  141.         else
  142.         {
  143.             int temp=size[ch[now][0]]+cnt[now];
  144.             if(x<=temp)return key[now];
  145.             else{x-=temp;now=ch[now][1];}
  146.         }
  147.     }
  148. }
  149. void input()
  150. {
  151.     int T=read<int>();
  152.     int opt,x;
  153.     while(T--)
  154.     {
  155.         opt=read<int>();x=read<int>();
  156.         if(opt==1)insert(x);
  157.         else if(opt==2)del(x);
  158.         else if(opt==3)printf("%d\n",find_order_of_key(x));
  159.         else if(opt==4)printf("%d\n",find_by_order(x));
  160.         else if(opt==5)
  161.         {
  162.             insert(x);
  163.             printf("%d\n",key[pre()]);
  164.             del(x);
  165.         }
  166.         else if(opt==6)
  167.         {
  168.             insert(x);
  169.             printf("%d\n",key[nex()]);
  170.             del(x);
  171.         }
  172.     }
  173. }
  174. int main()
  175. {
  176.     file();
  177.     input();
  178.     return 0;
  179. }

洛谷P3391 splay模板

题目描述

您需要写一种数据结构（可参考题目标题），来维护一个有序数列，其中需要提供以下操作：翻转一个区间，输出一行n个数字，表示原始序列经过m次变换后的结果

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. typedef int sign;
  4. typedef long long ll;
  5. #define For(i,a,b) for(register sign i=(sign)a;i<=(sign)b;++i)
  6. #define Fordown(i,a,b) for(register sign i=(sign)a;i>=(sign)b;--i)
  7. const int N=1e5+5;
  8. bool cmax(sign &a,sign b){return (a<b)?a=b,1:0;}
  9. bool cmin(sign &a,sign b){return (a>b)?a=b,1:0;}
  10. template<typename T>T read()
  11. {
  12.     T ans=0,f=1;
  13.     char ch=getchar();
  14.     while(!isdigit(ch)&&ch!='-')ch=getchar();
  15.     if(ch=='-')f=-1,ch=getchar();
  16.     while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch-'0'),ch=getchar();
  17.     return ans*f;
  18. }
  19. void file()
  20. {
  21.     #ifndef ONLINE_JUDGE
  22.         freopen("splay.in","r",stdin);
  23.         freopen("splay.out","w",stdout);
  24.     #endif
  25. }
  26. int ch[N][2],fa[N],size[N],rev[N],root,sz;
  27. inline int get(int x){return x==ch[fa[x]][1];}
  28. inline void update(int x){size[x]=1+size[ch[x][0]]+size[ch[x][1]];}
  29. inline void rotate(int x,int &k)
  30. {
  31.     int old=fa[x],oldfa=fa[old],o=get(x);
  32.     if(k==old)k=x;
  33.     else ch[oldfa][ch[oldfa][1]==old]=x;
  34.     fa[x]=oldfa;fa[old]=x;fa[ch[x][o^1]]=old;
  35.     ch[old][o]=ch[x][o^1];ch[x][o^1]=old;
  36.     update(x),update(old);
  37. }
  38. inline void splay(int x,int &k)
  39. {
  40.     while(x!=k)
  41.     {
  42.         if(fa[x]!=k)rotate(get(x)^get(fa[x])?x:fa[x],k);
  43.         //printf("%d %d\n",x,k);
  44.         rotate(x,k);
  45.     }
  46. }
  47. #define mid ((l+r)>>1)
  48. inline void build(int l,int r,int pre)
  49. {
  50.     if(l>r)return;
  51.     ch[pre][mid>=pre]=mid;
  52.     fa[mid]=pre;size[mid]=1;
  53.     if(l==r)return;
  54.     build(l,mid-1,mid);build(mid+1,r,mid);
  55.     update(mid);
  56. }
  57. #undef mid
  58. int n,m;
  59. void input(){n=read<int>();m=read<int>();}
  60. inline void rever(int x)
  61. {
  62.     swap(ch[x][0],ch[x][1]);
  63.     rev[ch[x][0]]^=1;rev[ch[x][1]]^=1;
  64.     rev[x]=0;
  65. }
  66. int find(int x)
  67. {
  68.     int now=root;
  69.     while(1)
  70.     {
  71.         if(rev[now])rever(now);
  72.         if(size[ch[now][0]]>=x)now=ch[now][0];
  73.         else
  74.         {
  75.             if(size[ch[now][0]]==x-1)return now;
  76.             x=x-size[ch[now][0]]-1;
  77.             now=ch[now][1];
  78.         }
  79.     }
  80. }
  81. void work()
  82. {
  83.     int l,r;
  84.     root=(n+3)>>1;
  85.     build(1,n+2,root);
  86.     fa[root]=0;
  87.     while(m--)
  88.     {
  89.         l=read<int>();r=read<int>();
  90.         l=find(l);r=find(r+2);
  91.         splay(l,root);splay(r,ch[l][1]);
  92.         rev[ch[r][0]]^=1;
  93.     }
  94. }
  95. void out(int x)
  96. {
  97.     if(rev[x])rever(x);
  98.     if(ch[x][0])out(ch[x][0]);
  99.     if(x>1&&x<n+2)printf("%d ",x-1);
  100.     if(ch[x][1])out(ch[x][1]);
  101. }
  102. int main()
  103. {
  104.     file();
  105.     input();
  106.     work();
  107.     out(root);
  108.     return 0;
  109. }

另外推荐一篇写得好的博客

浅谈平衡树splay的更多相关文章

  1. 浅谈算法——splay

    BST(二叉查找树)是个有意思的东西,种类巨TM多,然后我们今天不讲其他的,我们今天就讲splay 首先,如果你不知道Splay是啥,你也得知道BST是啥 如上图就是一棵优美的BST,它对于每个点保证 ...

  2. 浅谈splay（点的操作）

    浅谈splay(点的操作) 一.基本概念 splay本质:二叉查找树 特点:结点x的左子树权值都小于x的权值,右子树权值都大于x的权值 维护信息: 整棵树:root 当前根节点  sz书上所有结点编号 ...

  3. 浅谈JAVA集合框架

    浅谈JAVA集合框架 Java提供了数种持有对象的方式,包括语言内置的Array,还有就是utilities中提供的容器类(container classes),又称群集类(collection cl ...

  4. 浅谈SQL Server数据内部表现形式

    在上篇文章 浅谈SQL Server内部运行机制 中,与大家分享了SQL Server内部运行机制,通过上次的分享,相信大家已经能解决如下几个问题: 1.SQL Server 体系结构由哪几部分组成? ...

  5. 浅谈SQL Server---1

    浅谈SQL Server优化要点 https://www.cnblogs.com/wangjiming/p/10123887.html 1.SQL Server 体系结构由哪几部分组成? 2.SQL ...

  6. cdq分治浅谈

    $cdq$分治浅谈 1.分治思想 分治实际上是一种思想,这种思想就是将一个大问题划分成为一些小问题,并且这些小问题与这个大问题在某中意义上是等价的. 2.普通分治与$cdq$分治的区别 普通分治与$c ...

  7. Lct浅谈

    Lct浅谈 1.对lct的认识 ​ 首先要知道$lct$是什么.$lct$的全称为$link-cut-tree$.通过全称可以看出,这个数据结构是维护树上的问题,并且是可以支持连边断边操作.$lct$ ...

  8. HTTP协议漫谈 C#实现图（Graph) C#实现二叉查找树 浅谈进程同步和互斥的概念 C#实现平衡多路查找树(B树)

    HTTP协议漫谈   简介 园子里已经有不少介绍HTTP的的好文章.对HTTP的一些细节介绍的比较好,所以本篇文章不会对HTTP的细节进行深究,而是从够高和更结构化的角度将HTTP协议的元素进行分类讲 ...

  9. 浅谈BST（二叉查找树）

    目录 BST的性质 BST的建立 BST的检索 BST的插入 BST求前驱/后继 BST的节点删除 复杂度 平衡树 BST的性质 树上每个节点上有个值,这个值叫关键码 每个节点的关键码大于其任意左侧子 ...

随机推荐

  1. Struts2将图片输出到页面

            在做CRUD的过程中,添加页面是个表单,表单里面有一项是上传头像文件.这样表单提交后,头像文件上传了. 但这个文件存的地址是本地硬盘的一个文件夹.在编辑页面要做这个头像的回显的话,就需 ...

  2. EZ 2017 12 17初二初三第一次膜你赛

    以后平时练习还是写一写吧. (题目搞来搞去太烦了,直接PDF存起来) T1 水题(???),主要是数据水,正解是设一个阙值,然而根本没人打.(暴力出奇迹) CODE #include<cstdi ...

  3. 阿里云代金券 - 双12疯了~~~ 4核8G 3M带宽只要1890元/3年

    阿里云双12大促简直疯了,4核8G 3M带宽只要1890元/3年,比双11疯狂多了,双11没有上车的赶快来买吧!!! 前去阿里云双12活动页面 截图如下: 从截图中可以看出,不仅4核8G降到了地板,1 ...

  4. 蓝牙重启case之：hardware error

    蓝牙的通信分为host和controller,host端发送数据和命令到controller,controller 上传event以及数据到host端,这要求上下两端的通信要求状态一致性. 当发生状态 ...

  5. libgdx学习记录4——舞台Stage

    libgdx总的来说是一个框架,而不是一个成熟的游戏引擎.Stage是其中一个比较好的封装,里面自带Camera.SpriteBatch等常用渲染绘图工具. 下面是一个简单的添加图片,并让镜头左右上下 ...

  6. Java容器类List、ArrayList、Vector及map、HashTable、HashMap的区别与用法

    Java容器类List.ArrayList.Vector及map.HashTable.HashMap的区别与用法 ArrayList 和Vector是采用数组方式存储数据,此数组元素数大于实际存储的数 ...

  7. Scala基础（1）

    Scala基础语法 声明与定义: val,常量声明                       val  x:T(把x声明成一个类型为T的常量)  x是变量的名字,T是变量的类型          v ...

  8. 利用HOG+SVM实现行人检测

    利用HOG+SVM实现行人检测 很久以前做的行人检测,现在稍加温习,上传记录一下. 首先解析视频,提取视频的每一帧形成图片存到磁盘.代码如下 import os import cv2 videos_s ...

  9. 《杜增强讲Unity之Tanks坦克大战》11-游戏流程控制

    11 游戏流程控制 使用协程来控制游戏流程 11.1 添加MessageText 首先添加一个Text来显示文字   image 设置GameMgr   image 11.2 游戏整体流程 下面Gam ...

  10. 4星|《流量池》：Luckin Coffee营销操盘手经验谈

    流量池:“急功近利”的流量布局.营销转化 作者是一线营销操盘手,全书是作者的经验总结,这样的作者在营销类图书中比较罕见,因此这本书非常有价值. 全书是写给巨头之外的企业营销人员看的,这样的企业的流量来 ...