GBDT原理
| 样本编号 | 花萼长度(cm) | 花萼宽度(cm) | 花瓣长度(cm) | 花瓣宽度 | 花的种类 |
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | 山鸢尾 |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | 山鸢尾 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 | 杂色鸢尾 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 | 杂色鸢尾 |
| 5 | 6.3 | 3.3 | 6.0 | 2.5 | 维吉尼亚鸢尾 |
| 6 | 5.8 | 2.7 | 5.1 | 1.9 | 维吉尼亚鸢尾 |
6个样本的三分类问题:
(1)三维向量标志样本的label:
[1,0,0] 表示样本属于山鸢尾,
[0,1,0] 表示样本属于杂色鸢尾,
[0,0,1] 表示属于维吉尼亚鸢尾
(2) 对每一个类训练一个CART Tree 模型: 三个树相互独立
山鸢尾类别训练一个 CART Tree 1。
杂色鸢尾训练一个 CART Tree 2 。
维吉尼亚鸢尾训练一个CART Tree 3
(3) 以样本1为例
针对CART Tree 1,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,1]
针对CART Tree 2,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,0]
针对CART Tree 3,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,0]
(4)CART Tree1生成:哪个特征最合适? 这个特征的什么特征值作为切分点?以CART Tree 1为例
1. 从这四个特征中找一个特征做为CART Tree1 的节点,遍历所有的可能值
1.1 第一个特征【长度】的第一个特征值【5.1cm】为例。
R1 为所有样本中花萼长度小于 5.1 cm 的样本集合,
R2 为所有样本当中花萼长度大于等于 5.1cm 的样本集合。

y1为R1样本的label均值:y1=1/1=1
y2为R2样本的label均值:y2=(1+0+0+0+0)/5=0.2
样本1属于R2的值为:(1-0.2)^2
样本2属于R1的值为:(1-1)^2
样本3属于R2的值为(0-0.2)^2
样本4属于R2的值为(0-0.2)^2
样本5属于R2的值为(0-0.2)^2
样本6属于R2的值为(0-0.2)^2
CART Tree 1在第一个特征【长度】的第一个特征值【5.1cm】的损失值为:(1-0.2)^2+ (1-1)^2 + (0-0.2)^2+(0-0.2)^2+(0-0.2)^2 +(0-0.2)^2= 0.84
1.2 第一个特征【长度】的第二个特征值【4.9cm】计算,损失值为:2.244189
1.3 遍历所有特征的特征值,查找最小的特征及特征值,特征花萼长度,特征值为5.1 cm。这个时候损失函数最小为 0.8
2. 预测函数
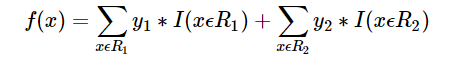
R1 = {2},R2 = {1,3,4,5,6},y1 = 1,y2 = 0.2
样本属于类别山鸢尾类别的预测值f1(x)=1+0.2∗5=2f1(x)=1+0.2∗5=2
同理我们可以得到对样本属于类别2,3的预测值f2(x)f2(x),f3(x)f3(x).样本属于类别1的概率 即为
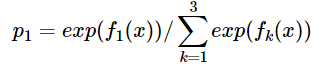
GBDT原理的更多相关文章
- GBDT原理及利用GBDT构造新的特征-Python实现
1. 背景 1.1 Gradient Boosting Gradient Boosting是一种Boosting的方法,它主要的思想是,每一次建立模型是在之前建立模型损失函数的梯度下降方向.损失函数是 ...
- 梯度提升树(GBDT)原理小结(转载)
在集成学习值Adaboost算法原理和代码小结(转载)中,我们对Boosting家族的Adaboost算法做了总结,本文就对Boosting家族中另一个重要的算法梯度提升树(Gradient Boos ...
- XGBoost,GBDT原理详解,与lightgbm比较
xgb原理: https://www.jianshu.com/p/7467e616f227 https://blog.csdn.net/a819825294/article/details/51206 ...
- 手撸GBDT原理(未完成)
一直对GBDT里面的具体计算逻辑不太清楚,在网上发现了一篇好博客. 先上总结的关系图 GBDT对类别变量是怎么处理的? 这些东西都是在网上发现的,讲的挺好的. GBDT原理与Sklearn源码分析-回 ...
- 机器学习入门:极度舒适的GBDT原理拆解
机器学习入门:极度舒适的GBDT拆解 本文旨用小例子+可视化的方式拆解GBDT原理中的每个步骤,使大家可以彻底理解GBDT Boosting→Gradient Boosting Boosting是集成 ...
- 梯度提升树(GBDT)原理小结
在集成学习之Adaboost算法原理小结中,我们对Boosting家族的Adaboost算法做了总结,本文就对Boosting家族中另一个重要的算法梯度提升树(Gradient Boosting De ...
- GBDT原理实例演示 1
考虑一个简单的例子来演示GBDT算法原理 下面是一个二分类问题,1表示可以考虑的相亲对象,0表示不考虑的相亲对象 特征维度有3个维度,分别对象 身高,金钱,颜值 cat dating.txt ...
- GBDT原理学习
首先推荐 刘建平 的博客学习算法原理推导,这位老师的讲解都很详细,不过GBDT的原理讲解我没看明白, 而是1.先看的https://blog.csdn.net/zpalyq110/article/de ...
- GBDT原理实例演示 2
一开始我们设定F(x)也就是每个样本的预测值是0(也可以做一定的随机化) Scores = { 0, 0, 0, 0, 0, 0, 0, 0} 那么我们先计算当前情况下的梯度值 ...
- GBDT原理详解
从提升树出发,——>回归提升树.二元分类.多元分类三个GBDT常见算法. 提升树 梯度提升树 回归提升树 二元分类 多元分类 面经 提升树 在说GBDT之前,先说说提升树(boosting tr ...
随机推荐
- Eclipse git 冲突合并
Eclipse有一个git的插件叫EGit,用于实现本地代码和远程代码对比.合并以及提交.但是在本地代码和远程代码有冲突的时候,EGit的处理方案还是有点复杂.今天就彻底把这些步骤给理清楚,并公开让一 ...
- kangle web配置phpmyadmin
1. kangle安装参考:https://www.kangleweb.com/thread-6001-1-1.html 2. 安装mysql-5.7.22:http://www.cnblogs.co ...
- JMeter学习(二十九)自动化badboy脚本开发技术(转载)
转载自 http://www.cnblogs.com/yangxia-test 一般人用badboy都是使用它的录制功能,其它badboy还是一款自动化的工具,它可以实现检查点.参数化.迭代.并发.报 ...
- python学习day6 for循环 字符串的内置方法
1.for循环 和while相比 l=[1,2,3] i=0 while i <len(l) print(l[i]) i+=1 l=['a','b','c'] for item in l: pr ...
- spark快速开发之scala基础之1 数据类型与容器
写在前面 面向java开发者.实际上,具有java基础学习scala是很容易.java也可以开发spark,并不比scala开发的spark程序慢.但学习scala可有助于更快更好的理解spark.比 ...
- java面试题:基础知识
类和对象 Q:讲一下面向对象OOP思想. 面向对象主要是抽象,封装,继承,多态. 多态又分为重载和重写.重载主要是方法参数类型不一样,重写则是方法内容不一样. Q:抽象类和接口有什么区别? 抽象类中可 ...
- POJ-1321.棋盘问题.(回溯)
做完题之后看了网上的一些题解但是发现他们的解释大部分都是错误的,所以就自己写了一下,笔者能力也有限,有错误之处大家多多指正. 第一次看题的时候以为就是简单的八皇后,但是写了之后发现存在很多问题,比如需 ...
- 创建文件指针数组c++
#include<fstream>using namespace std; void main(){ for (int i=0; i<=1; i++) { char szName[1 ...
- java_5.1 for循环
1.求1-100的和 public static void main(String[] args) { int sum = 0; for (int i = 0; i <= 100 ; i++) ...
- 线特征---EDLines原理(六)
参考文献:EDLines: A real-time line segment detector with a false detection control ----Cuneyt Akinlar , ...
