洛咕 P3756 [CQOI2017]老C的方块

四染色，贼好想

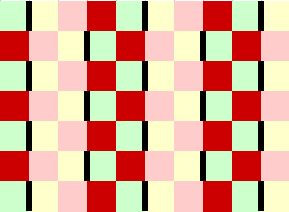
一个弃疗图形刚好对应一个红-绿-黄-粉色路线（不要吐槽颜色）

就是裸的最小割，建图傻逼懒得写了

#include<bits/stdc++.h>
#define il inline
#define vd void
typedef long long ll;
il int gi(){
    int x=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return x*f;
}
#define mp std::make_pair
std::map<std::pair<int,int>,int>M;
int X[100010],Y[100010],P[100010],S,T;
int fir[100010],head[100010],dep[100010],dis[10000010],nxt[10000010],w[10000010],id=1;
il vd link(int a,int b,int c){
    nxt[++id]=fir[a],fir[a]=id,dis[id]=b,w[id]=c;
    nxt[++id]=fir[b],fir[b]=id,dis[id]=a,w[id]=0;
}
il bool BFS(){
    static int que[100010],hd,tl;
    memset(dep,0,sizeof dep);
    hd=tl=0;que[tl++]=S;dep[S]=1;
    while(hd^tl){
        int x=que[hd++];
        for(int i=fir[x];i;i=nxt[i])
            if(!dep[dis[i]]&&w[i])
                dep[dis[i]]=dep[x]+1,que[tl++]=dis[i];
    }
    return dep[T];
}
il int Dinic(int x,int maxflow){
    if(x==T)return maxflow;
    int ret=0;
    for(int&i=head[x];i;i=nxt[i])
        if(w[i]&&dep[dis[i]]==dep[x]+1){
            int d=Dinic(dis[i],std::min(maxflow-ret,w[i]));
            w[i]-=d,w[i^1]+=d,ret+=d;
            if(ret==maxflow)break;
        }
     return ret;
}
int main(){
    gi(),gi();int n=gi();S=n+1,T=n+2;
    for(int i=1;i<=n;++i)X[i]=gi(),Y[i]=gi(),P[i]=gi(),M[mp(X[i],Y[i])]=i;
    for(int i=1;i<=n;++i)
        if(X[i]%4==0||X[i]%4==1){
            if((X[i]%4==1)==(Y[i]%2==1)){
                if(X[i]%4==1&&M.find(mp(X[i]+1,Y[i]))!=M.end())link(i,M[mp(X[i]+1,Y[i])],std::min(P[i],P[M[mp(X[i]+1,Y[i])]]));
                if(X[i]%4==0&&M.find(mp(X[i]-1,Y[i]))!=M.end())link(i,M[mp(X[i]-1,Y[i])],std::min(P[i],P[M[mp(X[i]-1,Y[i])]]));
                if(M.find(mp(X[i],Y[i]-1))!=M.end())link(M[mp(X[i],Y[i]-1)],i,1e9);
                if(M.find(mp(X[i],Y[i]+1))!=M.end())link(M[mp(X[i],Y[i]+1)],i,1e9);
                if(X[i]%4==0&&M.find(mp(X[i]+1,Y[i]))!=M.end())link(M[mp(X[i]+1,Y[i])],i,1e9);
                if(X[i]%4==1&&M.find(mp(X[i]-1,Y[i]))!=M.end())link(M[mp(X[i]-1,Y[i])],i,1e9);
            }else link(S,i,P[i]);
        }else{
            if((X[i]%4==2)==(Y[i]%2==1)){
                if(M.find(mp(X[i],Y[i]-1))!=M.end())link(i,M[mp(X[i],Y[i]-1)],1e9);
                if(M.find(mp(X[i],Y[i]+1))!=M.end())link(i,M[mp(X[i],Y[i]+1)],1e9);
                if(X[i]%4==2&&M.find(mp(X[i]+1,Y[i]))!=M.end())link(i,M[mp(X[i]+1,Y[i])],1e9);
                if(X[i]%4==3&&M.find(mp(X[i]-1,Y[i]))!=M.end())link(i,M[mp(X[i]-1,Y[i])],1e9);
            }else link(i,T,P[i]);
        }
    int ans=0;while(BFS())memcpy(head,fir,sizeof head),ans+=Dinic(S,1e9);
    printf("%d\n",ans);
    return 0;
}