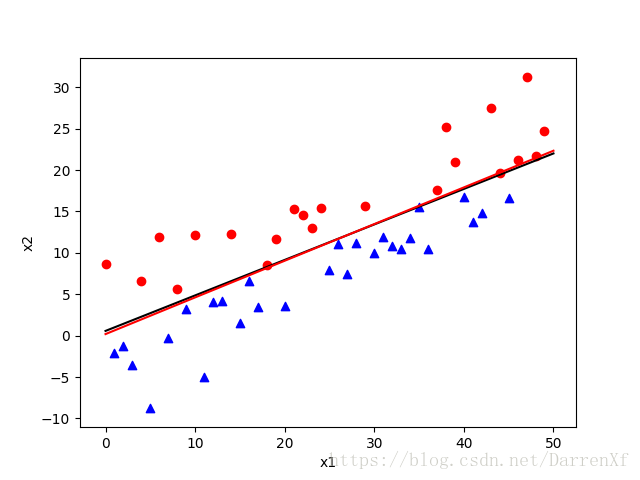
1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. import math
  5. def create_data(w1=3,w2=-7,b=4,seed=1,size=30):
  6.     np.random.seed(seed)
  7.     w = np.array([w1,w2])
  8.     x1 = np.arange(0,size)
  9.     v = np.random.normal(loc=0,scale=5,size=size)
  10.     x2 = v - (b+w[0]*x1)/(w[1]*1.0)
  11.     y_train=[]
  12.     x_train = np.array(zip(x1,x2))
  13.     for item in v:
  14.         if item >=0:
  15.             y_train.append(1)
  16.         else:
  17.             y_train.append(-1)
  18.     y_train = np.array(y_train)
  19.     return x_train,y_train
  21. def SGD(x_train,y_train):
  22.     alpha=0.01
  23.     w,b=np.array([0,0]),0
  24.     c,i=0,0
  25.     while i<len(x_train):
  26.         if (x_train[i].dot(w)+b)*y_train[i] <=0:
  27.             c +=1
  28.             w=w+alpha*y_train[i]*x_train[i]
  29.             b=b+alpha*y_train[i]
  30.             print("count:%s index:%s w:%s:b:%s" %(c,i,w,b))
  31.             i=0
  32.         else:
  33.             i=i+1
  34.     return w,b
  36. def test_and_show(w1,w2,b,size,w_estimate,b_estimate,x_train,y_train):
  37.     fig = plt.figure()
  38.     ax1 = fig.add_subplot(111)
  39.     plt.xlabel('x1')
  40.     plt.ylabel('x2')
  41.     x1 = np.arange(0,size+1,size)
  42.     x2 = -(b+w1*x1)/(w2*1.0)
  43.     ax1.plot(x1,x2,c="black")
  44.     x2 = -(b_estimate+w_estimate[0]*x1)/w_estimate[1]*1.0
  45.     ax1.plot(x1,x2,c="red")
  46.     for i in range(0,len(x_train)):
  47.         if y_train[i]>0:
  48.             ax1.scatter(x_train[i,0],x_train[i,1],c="r",marker='o')
  49.         else:
  50.             ax1.scatter(x_train[i,0],x_train[i,1],c="b",marker="^")
  51.     plt.show()
  53. if __name__ == '__main__':
  54.     w1,w2,b=3,-7,4
  55.     size=50
  56.     x_train,y_train=create_data(w1,w2,b,1,size)
  57.     w_estimate,b_estimate=SGD(x_train,y_train)
  58.     test_and_show(w1,w2,b,size,w_estimate,b_estimate,x_train,y_train)

  1. count:1 index:0 w:[0.         0.08693155]:b:0.01
  2. count:2 index:9 w:[-0.09        0.05511436]:b:0.0
  3. count:3 index:8 w:[-0.01        0.11106631]:b:0.01
  4. count:4 index:9 w:[-0.1         0.07924912]:b:0.0
  5. count:5 index:8 w:[-0.02        0.13520107]:b:0.01
  6. count:6 index:9 w:[-0.11        0.10338388]:b:0.0
  7. count:7 index:8 w:[-0.03        0.15933583]:b:0.01
  8. count:8 index:9 w:[-0.12        0.12751864]:b:0.0
  9. count:9 index:8 w:[-0.04        0.18347059]:b:0.01
  10. count:10 index:9 w:[-0.13       0.1516534]:b:0.0
  11. count:11 index:8 w:[-0.05        0.20760535]:b:0.01
  12. count:12 index:9 w:[-0.14        0.17578815]:b:0.0
  13. count:13 index:8 w:[-0.06        0.23174011]:b:0.01
  14. count:14 index:9 w:[-0.15        0.19992291]:b:0.0
  15. count:15 index:8 w:[-0.07        0.25587487]:b:0.01
  16. count:16 index:9 w:[-0.16        0.22405767]:b:0.0
  17. count:17 index:8 w:[-0.08        0.28000963]:b:0.01
  18. count:18 index:9 w:[-0.17        0.24819243]:b:0.0
  19. count:19 index:18 w:[0.01       0.33316026]:b:0.01
  20. count:20 index:7 w:[-0.06        0.33550632]:b:0.0
  21. count:21 index:9 w:[-0.15        0.30368913]:b:-0.01
  22. count:22 index:18 w:[0.03       0.38865696]:b:0.0
  23. count:23 index:7 w:[-0.04        0.39100302]:b:-0.01
  24. count:24 index:9 w:[-0.13        0.35918582]:b:-0.02
  25. count:25 index:16 w:[-0.29        0.29352152]:b:-0.03
  26. count:26 index:8 w:[-0.21        0.34947347]:b:-0.02
  27. count:27 index:18 w:[-0.03       0.4344413]:b:-0.01
  28. count:28 index:9 w:[-0.12        0.40262411]:b:-0.02
  29. count:29 index:9 w:[-0.21        0.37080691]:b:-0.03
  30. count:30 index:18 w:[-0.03        0.45577474]:b:-0.02
  31. count:31 index:9 w:[-0.12        0.42395755]:b:-0.03
  32. count:32 index:9 w:[-0.21        0.39214035]:b:-0.04
  33. count:33 index:18 w:[-0.03        0.47710818]:b:-0.03
  34. count:34 index:9 w:[-0.12        0.44529098]:b:-0.04
  35. count:35 index:9 w:[-0.21        0.41347379]:b:-0.05
  36. count:36 index:18 w:[-0.03        0.49844162]:b:-0.04
  37. count:37 index:9 w:[-0.12        0.46662442]:b:-0.05
  38. count:38 index:9 w:[-0.21        0.43480723]:b:-0.06
  39. count:39 index:18 w:[-0.03        0.51977506]:b:-0.05
  40. count:40 index:9 w:[-0.12        0.48795786]:b:-0.06
  41. count:41 index:9 w:[-0.21        0.45614067]:b:-0.07
  42. count:42 index:44 w:[0.23       0.65296677]:b:-0.06
  43. count:43 index:7 w:[0.16       0.65531283]:b:-0.07
  44. count:44 index:7 w:[0.09       0.65765889]:b:-0.08
  45. count:45 index:7 w:[0.02       0.66000495]:b:-0.09
  46. count:46 index:9 w:[-0.07        0.62818775]:b:-0.1
  47. count:47 index:9 w:[-0.16        0.59637056]:b:-0.11
  48. count:48 index:9 w:[-0.25        0.56455336]:b:-0.12
  49. count:49 index:44 w:[0.19       0.76137946]:b:-0.11
  50. count:50 index:7 w:[0.12       0.76372552]:b:-0.12
  51. count:51 index:7 w:[0.05       0.76607158]:b:-0.13
  52. count:52 index:7 w:[-0.02        0.76841764]:b:-0.14
  53. count:53 index:9 w:[-0.11        0.73660045]:b:-0.15
  54. count:54 index:9 w:[-0.2         0.70478325]:b:-0.16
  55. count:55 index:9 w:[-0.29        0.67296605]:b:-0.17
  56. count:56 index:35 w:[-0.64      0.517885]:b:-0.18
  57. count:57 index:8 w:[-0.56        0.57383695]:b:-0.17
  58. count:58 index:8 w:[-0.48        0.62978891]:b:-0.16
  59. count:59 index:8 w:[-0.4         0.68574086]:b:-0.15
  60. count:60 index:18 w:[-0.22        0.77070869]:b:-0.14
  61. count:61 index:9 w:[-0.31       0.7388915]:b:-0.15
  62. count:62 index:35 w:[-0.66        0.58381044]:b:-0.16
  63. count:63 index:8 w:[-0.58       0.6397624]:b:-0.15
  64. count:64 index:8 w:[-0.5         0.69571435]:b:-0.14
  65. count:65 index:8 w:[-0.42        0.75166631]:b:-0.13
  66. count:66 index:18 w:[-0.24        0.83663414]:b:-0.12
  67. count:67 index:9 w:[-0.33        0.80481694]:b:-0.13
  68. count:68 index:26 w:[-0.59       0.6938186]:b:-0.14
  69. count:69 index:8 w:[-0.51        0.74977055]:b:-0.13
  70. count:70 index:8 w:[-0.43       0.8057225]:b:-0.12
  71. count:71 index:18 w:[-0.25        0.89069034]:b:-0.11
  72. count:72 index:9 w:[-0.34        0.85887314]:b:-0.12
  73. count:73 index:16 w:[-0.5         0.79320884]:b:-0.13
  74. count:74 index:18 w:[-0.32        0.87817667]:b:-0.12
  75. count:75 index:16 w:[-0.48        0.81251236]:b:-0.13
  76. count:76 index:18 w:[-0.3         0.89748019]:b:-0.12
  77. count:77 index:9 w:[-0.39      0.865663]:b:-0.13
  78. count:78 index:44 w:[0.05      1.0624891]:b:-0.12
  79. count:79 index:9 w:[-0.04       1.0306719]:b:-0.13
  80. count:80 index:9 w:[-0.13        0.99885471]:b:-0.14
  81. count:81 index:9 w:[-0.22        0.96703751]:b:-0.15
  82. count:82 index:9 w:[-0.31        0.93522032]:b:-0.16
  83. count:83 index:9 w:[-0.4         0.90340312]:b:-0.17

神经网络 感知机 Perceptron python实现的更多相关文章

  1. 2. 感知机(Perceptron)基本形式和对偶形式实现

    1. 感知机原理(Perceptron) 2. 感知机(Perceptron)基本形式和对偶形式实现 3. 支持向量机(SVM)拉格朗日对偶性(KKT) 4. 支持向量机(SVM)原理 5. 支持向量 ...

  2. 吴裕雄 python 机器学习——人工神经网络感知机学习算法的应用

    import numpy as np from matplotlib import pyplot as plt from sklearn import neighbors, datasets from ...

  3. 感知机（python实现）

    感知机(perceptron)是二分类的线性分类模型,输入为实例的特征向量,输出为实例的类别(取+1和-1).感知机对应于输入空间中将实例划分为两类的分离超平面.感知机旨在求出该超平面,为求得超平面导 ...

  4. BP神经网络原理及python实现

    [废话外传]:终于要讲神经网络了,这个让我踏进机器学习大门,让我读研,改变我人生命运的四个字!话说那么一天,我在乱点百度,看到了这样的内容: 看到这么高大上,这么牛逼的定义,怎么能不让我这个技术宅男心 ...

  5. 20151227感知机(perceptron)

    1 感知机 1.1 感知机定义 感知机是一个二分类的线性分类模型,其生成一个分离超平面将实例的特征向量,输出为+1,-1.导入基于误分类的损失函数,利用梯度下降法对损失函数极小化,从而求得此超平面,该 ...

  6. 感知机(perceptron)概念与实现

    感知机(perceptron) 模型: 简答的说由输入空间(特征空间)到输出空间的如下函数: \[f(x)=sign(w\cdot x+b)\] 称为感知机,其中,\(w\)和\(b\)表示的是感知机 ...

  7. 神经网络(BP)算法Python实现及简单应用

    首先用Python实现简单地神经网络算法: import numpy as np # 定义tanh函数 def tanh(x): return np.tanh(x) # tanh函数的导数 def t ...

  8. 深层神经网络框架的python实现

    概述 本文demo非常适合入门AI与深度学习的同学,从最基础的知识讲起,只要有一点点的高等数学.统计学.矩阵的相关知识,相信大家完全可以看明白.程序的编写不借助任何第三方的深度学习库,从最底层写起. ...

  9. 机器学习(4):BP神经网络原理及其python实现

    BP神经网络是深度学习的重要基础,它是深度学习的重要前行算法之一,因此理解BP神经网络原理以及实现技巧非常有必要.接下来,我们对原理和实现展开讨论. 1.原理  有空再慢慢补上,请先参考老外一篇不错的 ...

随机推荐

  1. Docker宿主机管理

    不需要每次输入sudo 在当前用户的用户目录.bashrc中增加以下内容,此后使用docker命令时不需要每次都增加sudo. echo 'sudo usermod -aG docker $USER' ...

  2. zt:我使用过的Linux命令之ar - 创建静态库.a文件

    我使用过的Linux命令之ar - 创建静态库.a文件 本文链接:http://codingstandards.iteye.com/blog/1142358    (转载请注明出处) 用途说明 创建静 ...

  3. Marvell 88SE9215 AHCI驱动笔记

    禁止转载!禁止转载!禁止转载! 一.Marvell 88SE9215.AHCI与SATA简介 1.Marvell 88SE9215 1)概述 88SE9215是一个四端口,兼容3 Gbps和6 Gbp ...

  4. POJ3625Building Roads

    Building Roads Description Farmer John had just acquired several new farms! He wants to connect the ...

  5. JAVA语言程序设计课程评价

    紧张的又短暂的一个学期结束了,这个学期也许将成为我人生中一个重要的转折点,作为一名半路出家的选手,在初次了解Java语言时我感到非常的迷茫与不知所措.因为之前很多同学都是通过假期时间在家自学,刚转入新 ...

  6. 安卓学习记录（四）——体温表APP

    1.新建project file->new->new project,选择Basic Activity 2.在content_main.xml中添加一个List View 1 <Li ...

  7. PHP垃圾回收机制的一些浅薄理解

    相信只要入门学习过一点开发的同学都知道,不管任何编程语言,一个变量都会保存在内存中.其实,我们这些开发者就是在来回不停地操纵内存,相应地,我们如果一直增加新的变量,内存就会一直增加,如果没有一个好的机 ...

  8. express 路由匹配和数据获取

    express配置路由只需要通过app.method(url,func)来配置,其中url配置和其中的参数获取方法不同 直接写全路径 路由中允许存在. get请求传入的参数 router.get(&q ...

  9. HTML 网页开发、CSS 基础语法——九.CSS概述

    1.产生背景 从HTML的答案盛开时,样式就以各种形式存在,最初的HTML只i包含很少的显示属性.随着HTML的成长为了满足页面设计者的要求,HTML添加了许多显示功能,随着功能的增加HTML页面变得 ...

  10. 鸿蒙内核源码分析(文件概念篇) | 为什么说一切皆是文件 | 百篇博客分析OpenHarmony源码 | v62.01

    百篇博客系列篇.本篇为: v62.xx 鸿蒙内核源码分析(文件概念篇) | 为什么说一切皆是文件 | 51.c.h.o 本篇开始说文件系统,它是内核五大模块之一,甚至有Linux的设计哲学是" ...